Vector. Какво е вектор?

Подобно понятие като вектор се разглежда в почти всички естествени науки и може да има напълно различни значения, затова е невъзможно да се даде уникална дефиниция на вектор за всички области. Но нека се опитаме да го разберем. И така, какво е вектор?

Концепцията за вектор в класическата геометрия

Векторът в геометрията е сегмент, за който е посочено коя от точките е началото и кой е краят. По-просто казано, векторът е насочен сегмент.

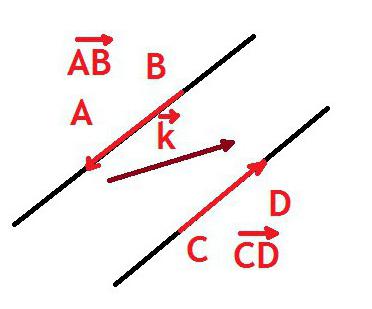
Съответно, векторът се обозначава (това, което се разглежда по-горе), както и сегментът, т.е. два с главни букви Латинска азбука с тире или стрелка, сочеща надясно отгоре. Можете също да го подпишете с малка (малка) буква на латинската азбука с тире или стрелка. Стрелката винаги е насочена надясно и не се променя в зависимост от местоположението на вектора.

По този начин векторът има посока и дължина.

Обозначението на вектора съдържа неговата посока. Това е изразено както на фигурата по-долу.

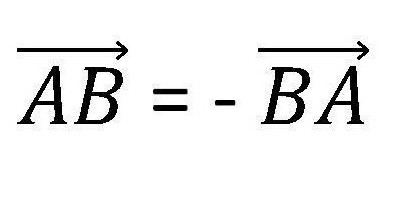
Промяната на посоката променя стойността на вектора на обратното.

Дължината на вектора е дължината на сегмента, от който се формира. Тя се обозначава като модул на вектор. Това е показано на фигурата по-долу.

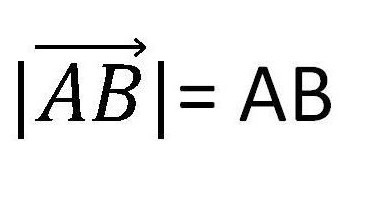
Съответно, нула е вектор, чиято дължина е нула. От това следва, че нулевият вектор е точка, а точките на начало и край съвпадат в него.

Дължината на вектора - стойността винаги не е отрицателна. С други думи, ако има сегмент, то той задължително има определена дължина или точка, тогава неговата дължина е равна на нула.

Понятието за точка е основно и няма определение.

Добавяне на вектор

Има специални формули и правила за вектори, с които можете да добавите.

Триъгълно правило. за векторни допълнения според това правило е достатъчно да се комбинира края на първия вектор и началото на втория, като се използва паралелен превод, и се свързват. Полученият трети вектор ще бъде равен на добавянето на другите два.

Правило за паралелограма. За добавяне съгласно това правило е необходимо двата вектора да се изчертаят от една точка и след това да се изтегли друг вектор от края на всеки. Това означава, че вторият ще бъде изтеглен от първия вектор, а първият - от втория. Резултатът е нова точка на пресичане и се образува паралелограма. Ако комбинираме точката на пресичане на началото и края на векторите, тогава полученият вектор ще бъде резултат от добавянето.

По същия начин е възможно да се извършва и изважда.

Векторна разлика

Подобно на добавянето на вектор, е възможно да се извадят. Тя се основава на принципа, показан на фигурата по-долу.

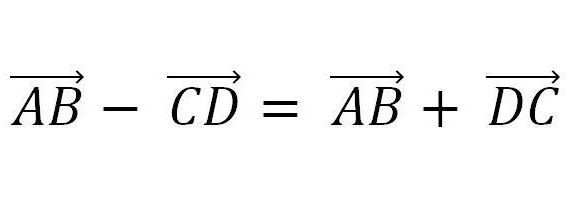
Това означава, че е достатъчно да се представи извадения вектор под формата на вектор, противоположен на него, и да се изчисли по принципите на добавяне.

Също така, абсолютно всеки ненулев вектор може да бъде умножен с произволно число k, което ще промени неговата дължина k пъти.

В допълнение към тях има и други формули на векторите (например, за да се изрази дължината на вектор през неговите координати).

Местоположение на векторите

Със сигурност много от тях са изправени пред подобна концепция като колинеен вектор. Какво е колинеарност?

Колинеарността на векторите е еквивалент на паралелните линии. Ако два вектора лежат на прави линии, които са успоредни един на друг, или на една права линия, тогава такива вектори се наричат ​​колинеарни.

Direction. По отношение един на друг, колинеарните вектори могат да бъдат ко-насочени или противоположно насочени, това се определя от посоката на векторите. Съответно, ако векторът е съвместно насочен с друг, тогава векторът, противоположен на него, е противоположно насочен.

Първата фигура показва два противоположно насочени вектора и третия, които не са колинеарни спрямо тях.

След въвеждането на горните свойства е възможно да се даде определение и равни вектори - това са вектори, които са насочени в една и съща посока и имат една и съща дължина на сегментите, от които са формирани.

В много науки се използва и понятието за радиус вектор. Такъв вектор описва позицията на една точка на равнината спрямо друга фиксирана точка (често това е произходът).

Вектори по физика

Да предположим, че при решаването на проблем възниква състояние: тялото се движи със скорост 3 m / s. Това означава, че тялото се движи със специфична посока в една права линия, така че тази променлива ще бъде векторна стойност. За решението е важно да се знае както стойността, така и посоката, тъй като в зависимост от разглеждането скоростта може да бъде равна на 3 m / s и -3 m / s.

Като цяло, векторът във физиката се използва, за да посочи посоката на силата, действаща върху тялото, и да определи резултата.

Когато тези сили са показани на фигурата, те са обозначени със стрелки с подписа на вектора над него. Класически дължината на стрелата е също толкова важна, с помощта на която те показват коя сила действа по-силно, но тази странична собственост не си струва да се разчита на нея.

Вектор в линейна алгебра и математически анализ

Елементите на линейните пространства също се наричат ​​вектори, но в този случай те са подредена система от числа, описващи някои от елементите. Следователно посоката в този случай вече няма значение. Векторна дефиниция в класическата геометрия и в математически анализ варират значително.

Проекционни вектори

Проектиран вектор - какво е това?

Доста често за правилно и удобно изчисление е необходимо да се разшири векторът в двуизмерно или триизмерно пространство, по осите на координатите. Тази операция е необходима, например, в механиката при изчисляване на силите, действащи върху тялото. Векторът във физиката се използва доста често.

За да се извърши проекция, достатъчно е да се понижат перпендикулярите от началото и края на вектора към всяка от координатните оси, получените по тях сегменти ще се наричат ​​проекция на вектора върху оста.

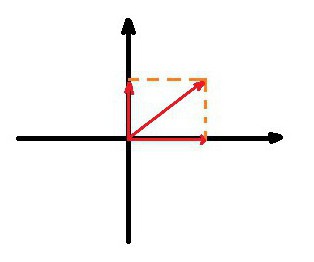
За да се изчисли дължината на проекцията, достатъчно е първоначалната му дължина да се умножи с определена тригонометрична функция, която се получава чрез решаване на мини-задача. По същество има правоъгълен триъгълник в която хипотенузата е оригинален вектор, единият от краката е проекция, а другият е спуснат перпендикулярно.