Движение на заредена частица в магнитно поле: формули. Движение на заредени частици в еднородно магнитно поле

Както е известно, електрическото поле обикновено се характеризира с големината на силата, с която тя действа върху изпитателната единица електрически заряд Магнитното поле традиционно се характеризира със сила, с която действа върху проводник с "единичен" ток. Въпреки това, тъй като тече, подредено движение на заредени частици се случва в магнитно поле. Следователно можем да определим магнитното поле В в някаква точка от пространството от гледна точка на магнитната сила F _B, която полето упражнява върху частицата, докато се движи в нея със скорост v.

Общи свойства на магнитната сила

Експерименти, при които се наблюдава движение на заредени частици в магнитно поле, дават следните резултати:

• Величината F _{B на} магнитната сила, действаща върху частицата, е пропорционална на заряда q и скоростта v на частицата.
• Ако движението на заредена частица в магнитно поле настъпва паралелно на вектора на това поле, тогава силата, действаща върху нея, е нула.
• Когато векторът за скоростта на частиците създава някакъв ъгъл θ 0 с магнитно поле, тогава силата действа в посока, перпендикулярна на v и B; F _{B е} перпендикулярна на равнината, образувана от v и B (виж фигурата по-долу).
• Величината и посоката на F _B зависи от скоростта на частиците и от величината и посоката на магнитното поле B.
• Посоката на силата, действаща върху положителния заряд, е противоположна на посоката на същата сила, действаща върху отрицателния заряд, движеща се в същата посока.
• Величината на магнитната сила, действаща върху движеща се частица, е пропорционална на греха θ на ъгъла θ между векторите v и B.

Силата на Лоренц

Можем да обобщим горните наблюдения чрез записване на магнитната сила като F _B = qv x B.

Когато една заредена частица се движи в магнитно поле, силата на Лоренц F _B с положителен q е насочена по векторния продукт vx B. По дефиниция, тя е перпендикулярна на v и B. Смятаме, че това уравнение е дефиницията за работа на магнитно поле в някаква точка в пространството. Тоест, тя се дефинира от гледна точка на силата, действаща върху частицата при нейното движение. По този начин движението на заредена частица в магнитно поле може кратко да бъде определено като движение под действието на тази сила.

Заряд, движещ се със скорост v в присъствието и на електрическото поле Е и на магнитното В, се влияе както от електрическата сила qE, така и от магнитния qv x B. Общият ефект, приложен към него, е F _L = qE + qv x B. така: пълната сила на Лоренц.

Движение на заредени частици в еднородно магнитно поле

Сега ще разгледаме специален случай на положително заредена частица, движеща се в еднородно поле, с начален вектор на скоростта, перпендикулярно на него. Да предположим, че векторът на полето B е насочен на страница. Фигурата по-долу показва, че частицата се движи в кръг в равнина, перпендикулярна на B.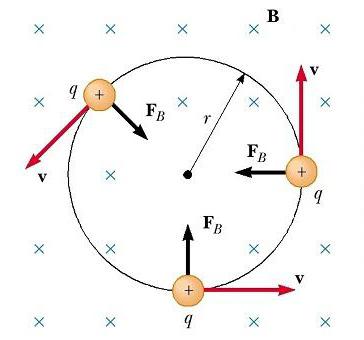

Кръговото движение на заредена частица в магнитно поле възниква, защото магнитната сила F _{B е} насочена под прав ъгъл към v и B и има постоянна стойност на qvB. Тъй като силата отклонява частиците, посоките v и F _{B се} променят непрекъснато, както е показано на фигурата. Тъй като F _B винаги е насочена към центъра на кръга, тя само променя посоката на v, а не нейната стойност. Както е показано на фигурата, движението на положително заредена частица в магнитно поле възниква обратно на часовниковата стрелка. Ако q е отрицателно, въртенето ще се извърши по часовниковата стрелка.

Динамика на кръговото движение на частица

Какви параметри характеризират описаното по-горе движение на заредена частица в магнитно поле? Формули за тяхното определяне, можем да получим, ако вземем предишното уравнение и приравним F _B центробежната сила, необходима за поддържане на кръговата траектория на движение: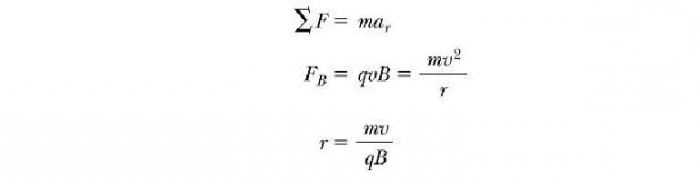

Това означава, че радиусът на кръга е пропорционален на инерцията mv на частицата и е обратно пропорционална на величината на заряда и магнитното поле. Ъгловата скорост на частиците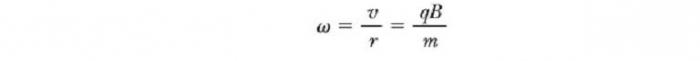

Периодът, в който заредена частица се движи в магнитно поле в кръг, е равна на окръжност, разделена на нейната линейна скорост: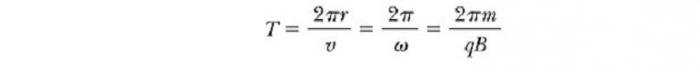

Тези резултати показват, че ъгловата скорост на частицата и периодът на кръговото движение не зависят от линейната скорост или от радиуса на орбитата. Ъгловата скорост ω често се нарича циклотрон. честота (кръгова), тъй като заредените частици циркулират с него в ускорител, наречен циклотрон.

Движение на частица под ъгъл спрямо вектора на магнитното поле

Ако векторът на скоростта на частиците v образува някакъв произволен ъгъл по отношение на вектора В, тогава неговата траектория е спирала. Например, ако еднакво поле е насочено по оста х, както е показано на фигурата по-долу, тогава няма компонент от магнитната сила F _B в тази посока. В резултат компонентът на ускорението е _х = 0 и х-компонентът на скоростта на частиците е постоянен. Въпреки това, магнитната сила F _B = qv x B причинява времево изменение на компонентите на скоростта v _y и v _z . В резултат на това една заредена частица се движи в магнитно поле по протежение на спирала, оста на която е успоредна на магнитното поле. Проекцията на траекторията върху yz равнината (когато се гледа по оста х) е окръжност. Проекциите му върху xy и xz равнините са синусоиди! Уравненията на движението остават същите, както по кръгова пътека, при условие че v се заменя с ν _⊥ = √ (ν _u ² + ν _z ² ).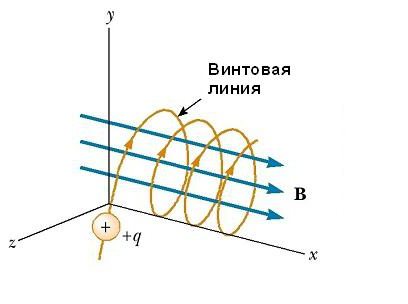

Нееднородно магнитно поле: как се движат частиците в него

Движението на заредена частица в магнитно поле, което е нехомогенно, възниква по сложни траектории. Така в поле, чиято величина се усилва в краищата на неговото съществуване и отслабва в средата си, както например е показано на фигурата по-долу, частица може да осцилира назад и напред между крайните точки. 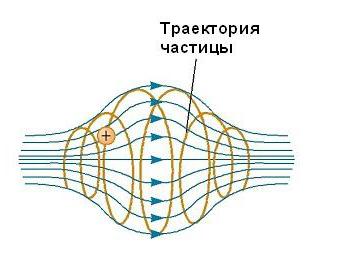Заредената частица започва от единия край на спиралата, навита по силата на силата и се движи по нея, докато достигне другия край, където се връща назад. Тази конфигурация е известна като "магнитна бутилка", защото заредените частици могат да бъдат затворени в нея. Използва се за ограничаване на плазмата, газ, състоящ се от йони и електрони. Такава схема на плазмено задържане може да играе ключова роля в контролирането на ядрения синтез, процес, който ни представя почти безкраен източник на енергия. За съжаление "магнитната бутилка" има свои собствени проблеми. Ако са уловени голям брой частици, сблъсъците между тях водят до изтичане на системата от системата.

Как Земята влияе върху движението на космическите частици

Повърхностните пояси на Van Allen се състоят от заредени частици (главно електрони и протони), обграждащи Земята под формата на тороидални области (виж фигурата по-долу). Движението на заредена частица в магнитното поле на Земята се осъществява по спирала около силовите линии от полюс до полюс, покривайки това разстояние за няколко секунди. Тези частици идват най-вече от Слънцето, но някои идват от звезди и други небесни обекти. Поради тази причина те се наричат ​​космически лъчи. Повечето от тях се отклоняват Магнитно поле на Земята и никога не достига до атмосферата. Въпреки това, някои от частиците попадат в капана, именно те съставляват колана на Ван Алън. Когато са над полюсите, те понякога се сблъскват с атоми в атмосферата, в резултат на което излъчват видима светлина. Така че в северното и южното полукълбо има красиви сияния. Те са склонни да се появяват в полярните региони, защото именно тук лентите на Ван Ален са разположени най-близо до повърхността на Земята.

Понякога обаче слънчева активност причинява по-голям брой заредени частици, влизащи в тези пояси, и значително нарушава нормалните сили на магнитното поле, свързани с Земята. В тези ситуации аврора понякога може да се види на по-ниски географски ширини.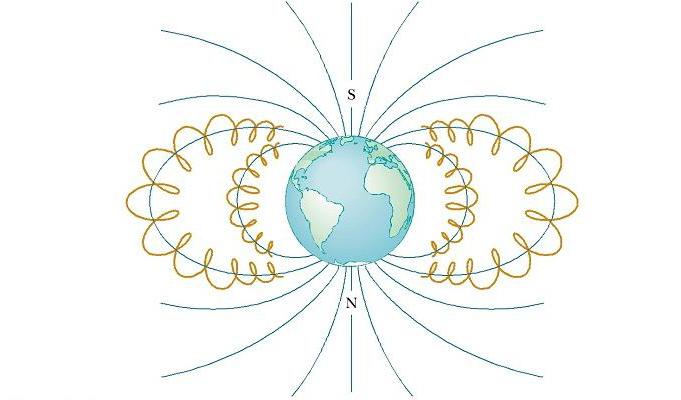

Селектор на скоростта

В много експерименти, при които движението на заредените частици се извършва в еднородно магнитно поле, е важно всички частици да се движат с почти същата скорост. Това може да бъде постигнато чрез прилагане на комбинация от електрическо поле и магнитно поле, ориентирани, както е показано на фигурата по-долу. Хомогенното електрическо поле е насочено вертикално надолу (в равнината на страницата) и същото магнитно поле се прилага в посока, перпендикулярна на електрическата (на страница). 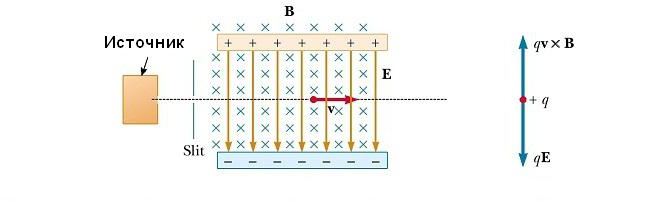За положително q магнитната сила F _B = qv x B е насочена нагоре и електрическата сила qE е надолу. Когато стойностите на две полета са избрани така, че qE = qvB, частицата се движи в права хоризонтална линия през областта. От израза qE = qvB откриваме, че само частици със скорост v = E / B преминават без отклонение чрез взаимно перпендикулярни електрически и магнитни полета. Силата F _В, действаща върху частици, движещи се със скорост по-голяма от v = E / B, се оказва по-електрическа и се отклонява нагоре. Тези, които се движат с по-ниска скорост, се отклоняват надолу.

Масспектрометър

Това устройство разделя йони в съответствие със съотношението на тяхната маса към зареждане. Според една версия на това устройство, известна като мас-спектрометър Bainbridge, йонният лъч първо преминава през селектора на скоростта и след това навлиза във второто B0 поле, което също е хомогенно и има същата посока като полето в селектора (виж фигурата по-долу) , След като влезете в него, движението на заредена частица в магнитно поле в полукръг с радиус r преди удара в фотографската плоча R. Ако йони са положително заредени, лъчът се отклонява нагоре, както е показано на фигурата. Ако йоните са отрицателно заредени, лъчът ще се отклони надолу. От израза за радиуса на кръговата траектория на частицата можем да намерим съотношението m / q

и след това, използвайки уравнението v = E / B, откриваме това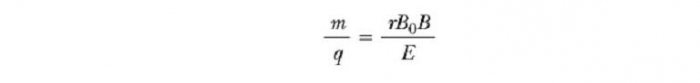

По този начин можем да определим m / q чрез измерване на радиуса на кривината, познавайки полетата на B, B ₀ и E. На практика това обикновено измерва масите на различни изотопи на даден йон, тъй като всички те носят един заряд q. По този начин, масовото съотношение може да бъде определено, дори ако q е неизвестно. Вариант на този метод е използван от J.J. Thomson (1856-1940) през 1897 г. за измерване на съотношението e / m _e за електроните.

циклотрон

Той може да ускори заредените частици до много високи скорости. И електрическите, и магнитните сили играят ключова роля тук. Получените високоенергийни частици се използват за бомбардиране на атомни ядра и по този начин произвеждат ядрени реакции, които представляват интерес за изследователите. Редица болници използват циклотронно оборудване за производството на радиоактивни вещества за диагностика и лечение.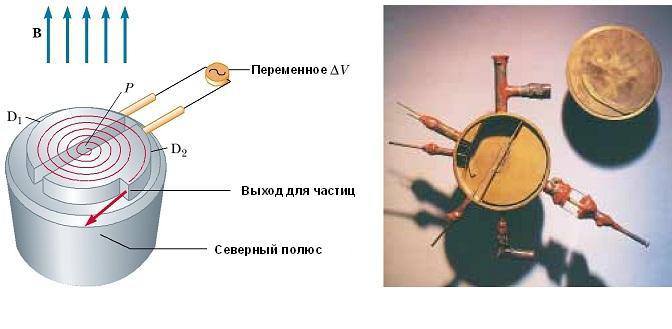

Схематично представяне на циклотрона е показано на фиг. по-долу. Частиците се движат вътре в два полуцилиндрични контейнера D1 и D2, наречени deants. Високочестотната променлива потенциална разлика се прилага към отделенията, разделени от пролука, а равномерното магнитно поле е насочено по оста на циклотрона (южният полюс на източника му не е показан на фигурата).

Положителният йон, освободен от източника в точка Р близо до центъра на устройството в първата двойка, се движи по полукръгла траектория (показана с пунктирана червена линия на фигурата) и се връща обратно в слота във време Т / 2, където Т е времето на една пълна революция вътре в два дуана ,

Честотата на приложената разлика в потенциала се регулира по такъв начин, че полярностите на диантите да се обърнат в момент, когато йонът излезе от един диант. Ако приложената разлика в потенциала се регулира по такъв начин, че в този момент D2 получава по-малък електрически потенциал от D1 чрез qΔV, то йонът се ускорява в процепа преди въвеждане на D ₂ , а кинетичната му енергия се увеличава с qΔV. След това се движи около D ₂ по полукръгла траектория с по-голям радиус (тъй като скоростта му се е увеличила).

След известно време Т / 2, той отново влиза в пропастта между деантите. В този момент поляритетите на дуентите отново се променят, а на йона се дава друг "удар" през пролуката. Движението на заредена частица в магнитно поле в спирала продължава, така че с всяко преминаване на един дуан йонът получава допълнителна кинетична енергия, равна на qΔV. Когато радиусът на неговата траектория стане близо до радиуса на дъгите, йонът напуска системата през изходния процеп. Важно е да се отбележи, че работата на циклотрона се основава на факта, че Т не зависи от скоростта на йона и радиуса на кръговата траектория. Можем да получим израз за кинетична енергия йон, когато напуска циклотрона, в зависимост от радиуса R на дес. Знаем, че скоростта на кръговото движение на частица е ν = qBR / m. Следователно, нейната кинетична енергия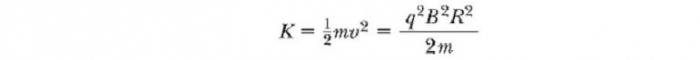

Когато енергията на йони в циклотрона надвишава около 20 МеВ, възникват релативистични ефекти. Отбелязваме, че Т нараства и че движещите се йони не остават във фаза с приложена потенциална разлика. Някои ускорители решават този проблем чрез промяна на периода на приложената потенциална разлика, така че остава във фаза с движещи се йони.

Ефект на Хол

Когато проводник с ток се постави в магнитно поле, се създава допълнителна потенциална разлика в посока, перпендикулярна на посоката на тока и магнитното поле. Това явление, за пръв път наблюдавано от Едуин Хол (1855-1938) през 1879 г., е известно като Хол. Винаги се наблюдава, когато заредена частица се движи в магнитно поле. Това води до отклонение на носителите на заряда от едната страна на проводника в резултат на магнитната сила, която те изпитват. Ефектът на Хол дава информация за знака на носителите на заряд и тяхната плътност, може да се използва и за измерване на магнитните полета.

Устройството за наблюдение на ефекта на Хол се състои от плосък проводник с ток I в посока х, както е показано на фигурата по-долу. 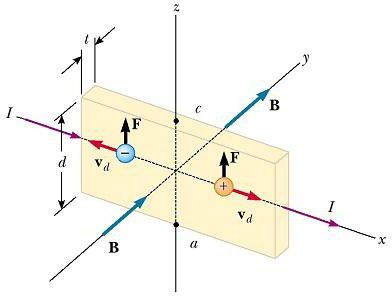Прилага се хомогенно поле В в посока y. Ако носителите на заряд са електрони, движещи се по оста х с скорост на отклонение v _d , тогава те получават насочена нагоре (като се има предвид отрицателната q) магнитна сила F _B = qv _d x B, отклонява се нагоре и се натрупва в горния край на плоския проводник, в резултат на което се получава излишък на положителен заряд се появява в долния край. Това натрупване на заряда в краищата се увеличава, докато електрическата сила, получена от разделяне на заряда, балансира магнитната сила, действаща върху носителите. Когато се достигне това равновесие, електроните вече не се отклоняват нагоре. Чувствителен волтметър или потенциометър, свързан с горния и долния ръб на проводника, може да измери разликата в потенциала, известна като напрежението в Хол.