Признаци на сходство на триъгълниците и тяхното практическо приложение за решаване на проблеми
Понятие за сходство произволно геометрични фигури по същество е много лесно да се обясни и още по-малко да се докаже. Така например, като гледаме обект през лупа, виждаме изображение на този обект, увеличено няколко пъти, със запазени пропорции на всичките му измерения. С други думи, изображението на обекта е подобно на оригиналния обект преди увеличението. В повечето геометрични проблеми, да се докаже пропорционалността на страните и триъгълни области нанесете основните 3 знака. За да се разгледат съществуващите признаци на сходство на триъгълниците, е необходимо първоначално да се определи ключовото понятие, което ще бъде използвано в текста в бъдеще.
Така че, триъгълниците са сходни, ако сходно разположените им страни са пропорционални, а съответно подредените ъгли са равни (заслужава да се помни, че страните са наречени подобни, или съответстващи, ако са разположени по същия начин). Разгледайте подобни триъгълници CABC и 1A 1 B 1 C 1 . Съгласно горното понятие съответните страни са: AB и A 1 B 1 , както и двойки страни BC и B 1 C 1 , AC и A 1 C 1 . Забележете, че страните на всяка от тези три двойки лежат противоположни ъгли от същата величина.
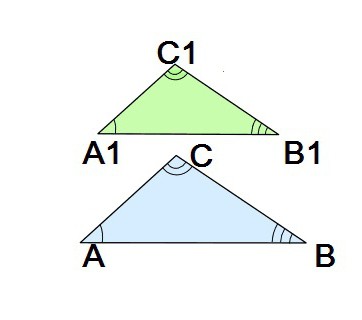Сходството се обозначава с специален характер което се поставя между обозначенията на въпросните цифри: CABC ∆ 1 A 1 B 1 C 1 .
Съотношението на съответните страни с наличието на тази характеристика е параметър, наречен коефициент на сходство k. Ако k = 2, тогава можем да кажем, че една от двете разглеждани геометрични фигури е увеличено двойно копие на другото. Ясно е, че ако k = 1, тогава триъгълниците са равни. По този начин това равенство може да се разглежда като специален случай на тяхната прилика.
Признаци на сходство на триъгълниците
Оказва се, че за да се установи наличието на разглежданата характеристика, не е необходимо да се проверяват всички изброени по-горе изисквания в текста на определението за сходство. Достатъчно е да изпълним минималните условия и сега ще потвърдим това на практика.
Първи знак
При решаването на проблемите първият знак за сходството на триъгълниците се появява в доказателствата много по-често от другите. Имайте предвид, че той работи само с два елемента с геометрична фигура: два ъгъла. Останалите признаци на сходство на триъгълниците изискват участието на три елемента. Така че, за два произволни подобни триъгълника, два ъгъла на една от тях са равни на едни и същи два ъгъла на другия.
Доказателство за
Според основните свойства, валидни за всеки произволен триъгълник, можем да напишем следния израз за .C. Нейната стойност ще бъде равна (180 ° - (+А + ∠В)), за друга 1С 1 стойността ще бъде изчислена по същия принцип. Чрез елементарни преобразувания на изрази получаваме, че =C = C 1 . По този начин всички ъгли в ВАВС са равни на всички аналогични ъгли, разположени в 1А 1 В 1 С 1 . По подобен алгоритъм се доказват останалите признаци на сходство на триъгълниците.
Втори знак
Този подход към доказателството често се използва, ако ъглите на разглежданите геометрични фигури са известни.
За два подобни триъгълника е вярно, че двете страни на всяка от тях са пропорционални на 2-ри подобни страни на другата, а ъглите между тези двойки страни са равни.
Доказателство за
За да докажете тази функция, трябва да се обърнете към предишните изчисления. Въз основа на горните резултати е достатъчно да се докаже, че =В = В 1 . Помислете за 2ABC 2 , за които, според първия знак, са валидни следните твърдения: = 1 = ∠А 1 , = 2 = В1. CABC 2 ~ 1А 1 В 1 С 1 . Това означава AB / A 1 B 1 = AC 2 / A 1 C. От друга страна, от условието е да се спазва следното отношение: AC / A 1 C 1 = AB / A 1 B 1 . В резултат се получава равенството на страните AC = AC 2 , както и твърдението, че CABC ~ ∆ABC 2 съгласно втория знак (AC = AC 2 и =A = ∠1, тъй като в резултат на разглеждането на първоначалните данни е установено, че A = 1A1 и = 1 = 1A1, AB- е обща страна за тези два триъгълника). От доказателството, че =B = ∠2, и тъй като = 2 = ∠V 1 , следва, че ∠В = В1. От което следва, че е доказан друг знак.
Трети знак
Тази характеристика се счита за най-очевидна, когато се доказва сходство, тъй като се разглеждат всички страни на тези триъгълници с известни параметри.
Така че, за два триъгълника, които са подобни един на друг, има твърдение, че 3 страни на една от тях са пропорционални на 3 съответни страни на другата.
Доказателство за
Като се има предвид предишната особеност на сходството, сега, за да се конструира доказателство, е достатъчно да се установи само, че съществува равенство на формата: =A = 1A 1 . За да направите това, разгледайте произволното ∆ABC 2 , за което ∠1 = 1A 1 , 2 = V 1 . Според първия атрибут CABC 2 ∆ ∆A 1 B 1 C 1 , за тези два триъгълника можем да запишем съотношението на типа AB / A 1 B 1 = BC 2 / B 1 C 1 = C 2 A / C 1 A 1, от което можем да напишем равенството на формата: B 1 C 1 = BC 2 , A 1 C 1 = AC 2 . От това логично е да се заключи, че CABC ∆ CABC 2, и като заключение, AndA и 1A1 са равни. От което следва, че разглежданата характеристика също е доказана.
свойства
- За два триъгълника, подобни един на друг, съотношението на стойностите на техните площи е право пропорционално на квадрата на коефициента. Доказателство. Помислете за две произволни фигури, имащи три страни и три ъгъла, които са подобни една на друга. Нека A и A 1 са съответните страни на тези фигури, а h и h 1 - съответните височини. Нека k е коефициентът на подобие за разглежданите триъгълници, следователно от аспектното съотношение можем да напишем уравнение на вида: A 1 = k * A. Лесно е да се види, че за съотношението на височините можем да напишем уравнение на формата: h 1 = k * h. За съотношението на площите на разглежданите геометрични фигури получаваме: S 1 / S = (1 / 2a 1 h 1 ) / (1 / 2ah) = (a 1 / a) * (h 1 / h) = k * k = k 2 . Така, когато триъгълник е „разтегнат” с 2 пъти, неговата площ се увеличава с 2 2 = 4 пъти. Второто свойство следва от предишното доказателство и е пряко свързано с него.
- Всички съответни линии, изчертани в такива триъгълници, също са пропорционални един на друг и са равни на стойността на показания по-горе коефициент. Това означава, че според горното имущество може да се твърди, че всички вътрешни допълнителни конструкции също ще бъдат пропорционални.
Добавяне на основния списък на знаците
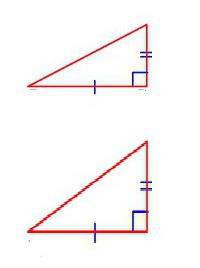
Струва си да разгледаме редица индивидуални особености, които са приложими за геометрични форми на определен тип. Така че правилните триъгълници са подобни, ако:
- хипотенузата и всеки от двата крака са съответно пропорционални;
- ако съответните им остри ъгли са равни;
- ако всички крака на разглежданите триъгълници са двойно пропорционални.
заключение
Така сме събрали всички възможни знаци, с помощта на които може някак да се докаже сходството на две или повече фигури с три ъгъла и страни, независимо от техния вид и свойства. При повечето проблеми в геометрията основните три знака се използват, за да се докаже пропорционалността на страните и областите, но не сме пренебрегнали редица знаци за сходство, които са приложими само ако е необходимо да се направи доказателство за въпросните геометрични фигури под прав ъгъл. Тези признаци на сходство прави триъгълници значително опростява процеса на решаване на различни видове задачи и изисква минимално количество данни за тях.