Височина на пирамидата: определение, формули, изчисления

Една от обемните фигури, изучавани в хода на пространствената геометрия, е пирамидата. Важна характеристика на тази цифра е нейната височина. В статията ще дадем определение на височината на пирамидата и ще дадем формулите, чрез които тя е свързана с други линейни характеристики.

Какво е пирамида

Под пирамидата се разбира геометричната форма на пространствената, която се получава чрез свързване на всички ъгли на полигона с една точка в пространството. Фигурата по-долу показва подреждането на линиите (ръбовете) на четириъгълните и петоъгълните пирамиди.

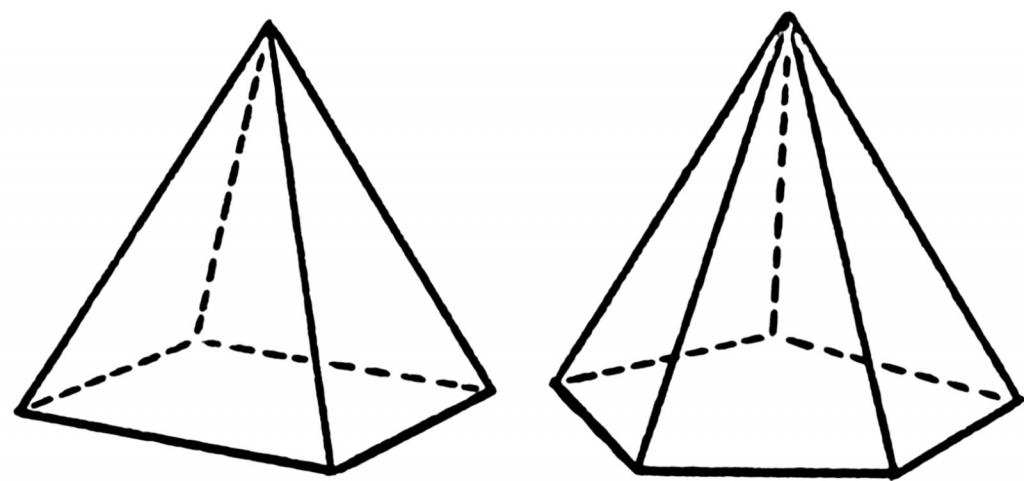
Многоъгълното лице на формата се нарича неговата основа. Точката, където всички триъгълни лица се свързват, се нарича връх. За да се определи височината на пирамидата, маркираните елементи са важни.

Височина на тялото

Височината на пирамидата се нарича перпендикулярна, която от върха се спуска в равнината на основата. Важно е да се разбере, че от всеки връх, принадлежащ на основата на фигурата, също е възможно да се начертае перпендикуляр на съответната триъгълна повърхност, но тя няма да изглежда толкова висока. Височината на пирамидата е единствената перпендикулярна, която е една от важните й линейни характеристики.

Всеки ученик знае, че всяка плоска фигура притежава геометричен център (във физиката съответства на центъра на масата). Например, геометричният център на произволен триъгълник се определя от точката на пресичане на нейните медиани, за паралелограма, точката на пресичане на диагоналите. Ако височината на пирамидата пресича основата му в геометричния център, тогава цифрата се нарича права линия. Пирамидата е права, с основен полигон със същите страни и ъгли, наречен правилен.

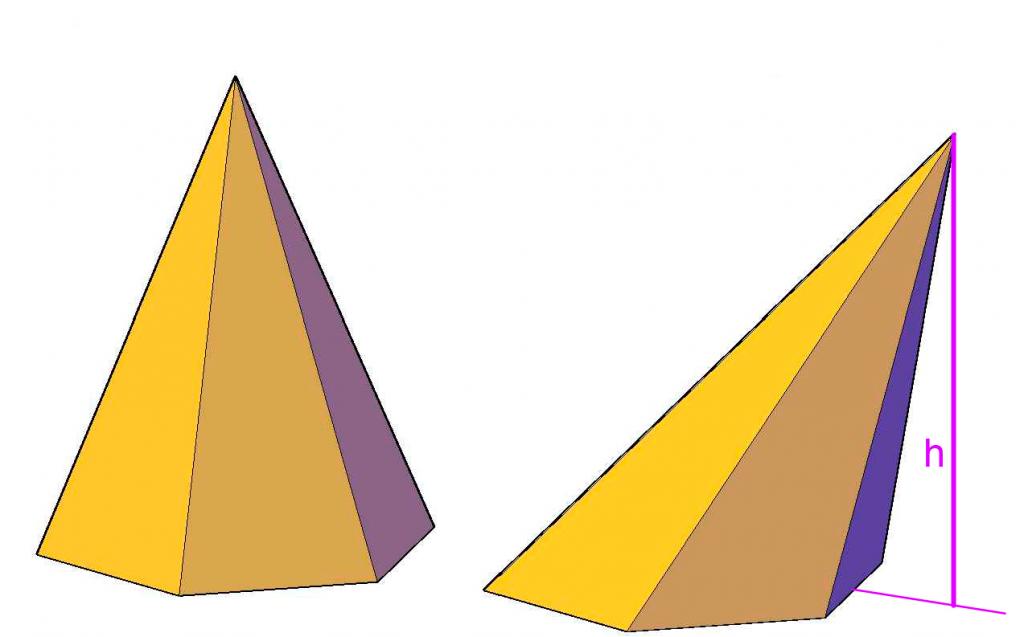
Фигурата по-горе показва разликата между грешната пирамида и правилната пирамида. Вижда се, че височината на неправилната форма лежи отвъд неговата основа, докато в правилната шестоъгълна пирамида височината е във формата, пресичаща основата му в геометричния център.

Важни свойства на всички нормални пирамиди са следните:

• всички странични повърхности са равнобедрени триъгълници и са равни една на друга;
• дължините на страничните ребра и апотема са еднакви.

Формули за височината на нормална пирамида

За всяка правилна пирамида има четири основни линейни характеристики:

• страна на основата;
• страничен ръб;
• апотема на страничната страна;
• височина на фигурата.

Всички те са математически свързани помежду си. Дължината на страната на основата се обозначава с а, височина - h, apothem - h _b и edge - b. Формулите, които свързват тези количества, имат индивидуален вид за съответната п-въглищна пирамида. Например, за нормална пирамида, четириъгълната височина може да се определи по формулите:

h = √ (a _b ² - a 2/4);

h = √ (b ² - a 2/2).

Тези формули произтичат от Питагоровата теорема при разглеждане на съответните правоъгълни триъгълници вътре в пирамидата.

Ако се вземе предвид фигура с триъгълна база, следващите формули са валидни за височината на нормалната пирамида:

h = √ (a _b ² - a 2/12);

h = √ (b ² - a 2/3).

Решение на проблема с шестоъгълна пирамида

Да предположим, че ни е дадена нормална пирамида с шестоъгълна основа. Известно е, че височината на основата на пирамидата е 13 см. Знаейки, че дължината на страничния му ръб е 10 см, е необходимо да се изчисли обемът и височината на правилната шестоъгълна пирамида.

Фигурата по-долу показва как изглежда нормален шестоъгълник.

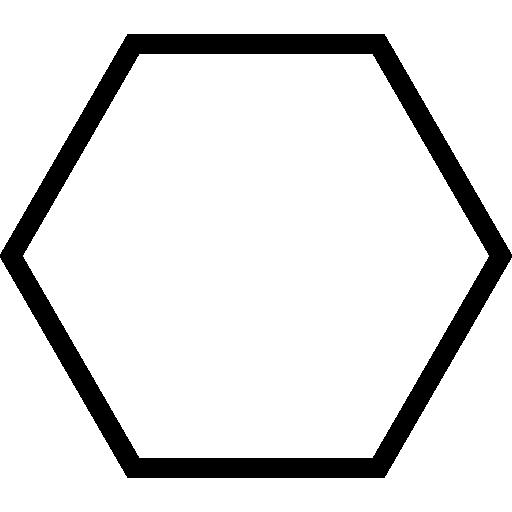
Разстоянието между двете си успоредни страни се нарича височина. Не е трудно да се покаже, че тази височина h _a е свързана с дължината на страната на фигурата със следната формула:

h _a = a * .3

Подставяйки стойността на h _a в израза, откриваме, че основната страна на a е равна на 7,51 cm.

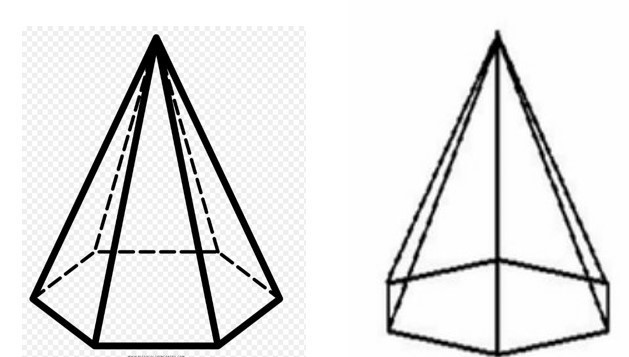
Височината h на фигурата може да се определи, ако разгледаме правоъгълен триъгълник вътре в пирамидата и състоящ се от два крака (височината на пирамидата и половината от диагонала на шестоъгълната основа) и хипотенузата (страничен ръб). Тогава стойността на h ще бъде равна на:

h = √ (b ² - a ² ) = √ (100 - 56,4) = 6,6 cm.

Обемът на пирамидата се определя като третата част от произведението на височината на фигурата върху площта на основата му. Площта на правилния шестоъгълник е:

S ₆ = n / 4 * a ² * ctg (pi / n) = 6/4 * a ² * ctg (pi / 6) = 3 * 3/2 * a ² = 3 * 3/2 * 56, 4 ≈ 146,53 cm ² .

Формулата, използвана за изчисляване на S6, е универсална за произволен нормален n-гон.

За да се определи обемът на фигурата, остава да се заменят параметрите, намерени в подходящата формула:

V = 1/3 * h * S6 = 1/3 * 6.6 * 146.53 = 322.366 cm3.

Получихме стойността на височината на пирамидата и изчислихме нейния обем. По този начин проблемът е решен.