Как да намерим прости числа?

Числата са различни: естествени, естествени, рационални, целочислени и дробни, положителни и отрицателни, сложни и прости, нечетни и четни, реални и др.

Какви числа се наричат ​​английската дума "simpl"?

Много често учениците на един от най-неусложните на пръв поглед въпроси на математиката, за това какво е простото число, не знаят как да отговорят. Те често бъркат прости числа с естествени числа (т.е. числата, които хората използват при преброяване на статии, докато в някои източници те започват от нула, а в други - от един). Но това са напълно две различни неща. Първичните числа са естествени, т.е. цели числа и положителни числа, които са по-големи от една и имат само 2 естествени разделители. В този случай един от тези делители е дадено число, а второто е едно. Например, три е просто число, тъй като не се дели на никой друг номер, различен от него и от него.

Съединени числа

Обратното на прости числа е съединение. Те също са естествени, също повече от една, но не са две, а по-голям брой разделители. Например, числата 4, 6, 8, 9 и т.н. са естествени, композитни, но не и прости числа. Както виждате, това са предимно четни числа, но не всички. Но „две“ - четно число и „първо число“ в серията от прости числа.

последователност

За да се изгради серия от прости числа, е необходимо да се направи селекция от всички естествени числа, като се вземе предвид тяхната дефиниция, т.е. трябва да действате от обратното. Необходимо е да се разгледа всяко от положителните числа, за да се определи дали има повече от два разделителя. Нека се опитаме да изградим поредица (последователност), която съставя прости числа. Списъкът започва с две, следващият е три, защото е разделен само на себе си и на единици. Помислете за номер четири. Има ли разделители освен четири и едно? Да, този номер е 2. Така че четири не е просто число. Пет е също просто (не се дели на никое друго число освен 1 и 5), но шест са делими. И като цяло, ако следвате всички четни числа, можете да видите, че с изключение на „две“, нито една от тях не е проста. Оттук стигаме до заключението, че четни числа, с изключение на две, не са прости. Друго откритие: всички числа, делими на три, с изключение на самата триада, независимо дали е четно или нечетно, също не са прости (6, 9, 12, 15, 18, 21, 24, 27 и т.н.). Същото се отнася и за числа, които са разделени на пет и седем. Всички те също не са прости. Нека обобщим. Така че, всички цифри са всички нечетни числа с изключение на едно и девет, а от четно - само „две“. Самите десетки (10, 20, ... 40 и т.н.) не са прости. Двуцифрени, трицифрени и т.н. прости числа могат да се определят въз основа на принципите, описани по-горе: ако те нямат други делители, различни от себе си и такива.

Теории за свойствата на простите числа

Има наука, която изучава свойствата на числата, включително и прости числа. Това е клон на математиката, който се нарича най-висок. В допълнение към свойствата на числа, той се занимава и с алгебрични, трансцендентни числа, както и с функции от различен произход, свързани с аритметиката на тези числа. В тези изследвания, в допълнение към елементарните и алгебричните методи, се използват и аналитични и геометрични. По-конкретно, изучаването на прости числа, включени в теорията на числата.

Основните числа са „градивни елементи“ на естествените числа.

В аритметиката има една теорема, която се нарича основна. Според него всяко естествено число, с изключение на едно, може да се представи като продукт, чиито фактори са прости числа, а последователността на факторите е уникална, което означава, че начинът на представяне е уникален. Нарича се декомпозирането на естественото число в прости фактори. Има и друго име за този процес - факторизация на числата. Като се изхожда от това, прости числа могат да бъдат наречени „строителни материали“, „блокове“ за изграждане на естествени числа.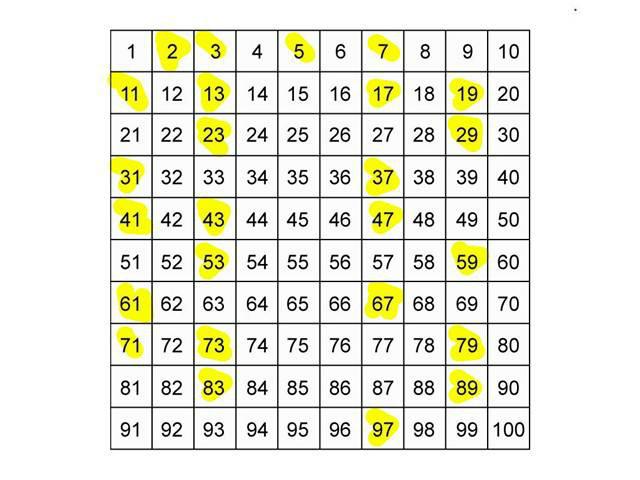

Търсене на прости числа. Тестове за простота

Много учени от различно време се опитаха да намерят някои принципи (системи) за намиране на списък с прости числа. Науката познава системи, които се наричат ​​сито Аткин, сито Сундартам и сито Ератостен. Въпреки това, те не дават никакви значими резултати и се използва проста проверка, за да се намерят прости числа. Също така математиците са създали алгоритми. Те се наричат ​​тестове за простота. Например, тестът е разработен от Рабин и Милър. Използва се от криптографи. Има и тест Kayal-Agraval-Sasken. Въпреки това, въпреки достатъчната й точност, е много трудно да се изчисли, което отклонява практическата му стойност.

Има ли набор от прости числа има лимит?

Фактът, че множеството от прости е безкрайност, пише в книгата "Принципи" древногръцки учен Евклид. Той каза следното: „Нека си представим за момент, че първичните числа имат граница. Тогава нека ги умножим един с друг и добавете един към продукта. Броят, получен в резултат на тези прости действия, не може да бъде разделен на един от няколко прости числа, защото винаги ще има един в останалите. А това означава, че има друг номер, който все още не е включен в списъка на простите числа. Следователно, нашето предположение не е вярно и този набор не може да има граница. В допълнение към доказателството за Евклид, има по-съвременна формула, дадена от швейцарския математик Леонард Ойлер от XVIII век. Според него сумата, обратна на сумата на първите n числа, нараства без ограничение, когато числото n расте. Но формулата на теоремата за разпределението на прости числа: (n) расте като n / ln (n).

Какво е най-голямото просто число?

Същият Леонард Ойлер успя да намери най-големия премиер за своето време. Това е 2 ³¹ - 1 = 2147483647. Въпреки това, до 2013 г. е изчислена другата най-точна в списъка на простите числа, 2 ^57885161 - 1, която се нарича номер на Мерсен. Той съдържа около 17 милиона десетични цифри. Както виждате, броят на учените от осемнадесети век е няколко пъти по-малък от този. Трябваше да е така, защото Ойлер правеше това изчисление ръчно, но нашият компютър вероятно беше подпомогнат от нашия съвременен. Освен това, този брой е получен на факултета по математика в един от американските факултети. Цифрите, кръстени на този учен, преминават през теста за простота на Лука-Лемере. Но науката не иска да спира дотук. Фондация Electronic Frontier, основана през 1990 г. в Съединените американски щати (EFF), назначи парична награда за намиране на големи прости числа. И ако до 2013 г. наградата се разчиташе на онези учени, които щяха да ги намерят сред 1 и 10 милиона десетични числа, днес тази цифра е достигнала от 100 милиона до 1 милиард. Размерът на наградите варира от 150 до 250 хиляди щатски долара.

Имена на специални прости числа

Тези числа, които бяха открити благодарение на алгоритмите, създадени от един или друг учен и преминали теста за простота, се наричат ​​специални. Ето някои от тях:

1. Merssen.

2. Wooda.

3. Ферма.

4. Кълън.

5. Прота.

6. Mills et al.

Опростеността на тези числа, наречена на горните учени, се установява чрез следните тестове:

1. Luc-Lemer.

2. Пепин.

3. Rizel.

4. Билхарт - Лемера - Селфиридж и др.

Съвременната наука не спира дотук и вероятно в близко бъдеще светът ще знае имената на онези, които биха могли да получат награда от $ 250,000, намирайки най-голямото просто число.