Как е формулирана и доказана косинусната теорема?
Не всички ученици и още повече възрастни знаят, че косинусната теорема е пряко свързана с Питагоровата теорема. По-точно, последното е специален случай на първия. Този момент, както и два начина да се докаже косинусната теорема, ще ви помогне да станете по-осведомен човек. В допълнение, практиката на изразяване на ценности от оригиналните изрази е добре развито логическо мислене. Дългата формула на изследваната теорема със сигурност ще принуди човек да работи и да се подобрява.
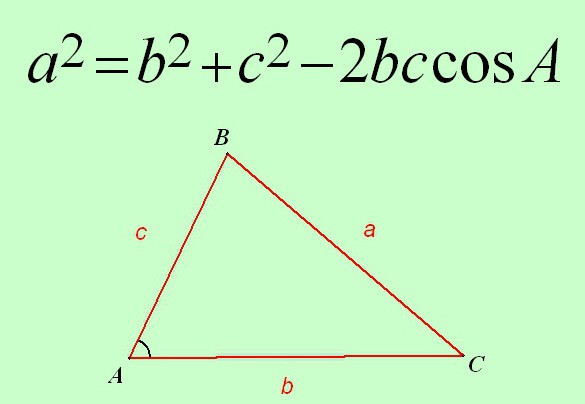
Началото на разговора: въвеждането на символи
Тази теорема е формулирана и доказана за произволен триъгълник. Следователно, тя винаги може да се използва във всяка ситуация, ако са дадени две страни, а в някои случаи три и един ъгъл, а не непременно между тях. каквото вид триъгълник теоремата винаги работи.
А сега за обозначаването на количества във всички изрази. По-добре е да се съгласите веднага, за да не го обяснявате няколко пъти. За тази цел е съставена следната таблица.
| Елемент от триъгълник | Неговото обозначение |
| Неизвестна страна | и |
| Две други страни | в, с |
| Ъгъл срещу непозната страна | А |
| Ъгли, които лежат срещу други страни | В, С |
| Височината на върха на триъгълника | п |
Формулиране и математическо писане
Така, косинусната теорема е формулирана по следния начин:
Квадратът на страната на всеки триъгълник е равен на сумата от квадратите на другите две страни на нея, минус два пъти произведението на същите страни от косинуса на ъгъла, който лежи между тях.
Разбира се, той е дълъг, но ако разбереш същността му, то тогава ще бъде лесно да се запомни. Можете дори да си представите рисунка на триъгълник. Визуално винаги е по-лесно да се запомни.
Формулата на тази теорема ще изглежда така:
a 2 = 2 + s 2 - 2 * c * s * cos A.
Малко дълго, но всичко е логично. Ако погледнете малко по-близо, можете да видите, че буквите се повтарят, така че е лесно да се запомни.
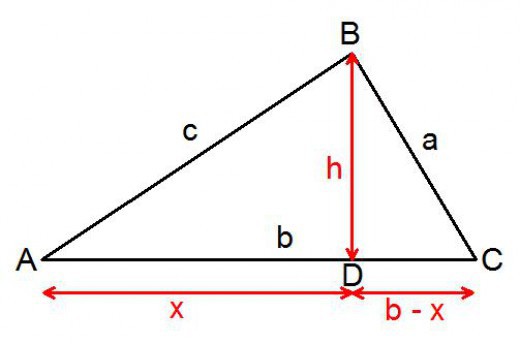
Общо доказателство на теоремата
Тъй като е валиден за всички триъгълници, е възможно да се избере за аргументацията на всеки от типовете. Нека да е фигура с всички остри ъгли. Помислете за произволен остър триъгълник, чийто ъгъл С е по-голям от ъгъл Б. От върха с този голям ъгъл трябва да спуснете перпендикуляра към противоположната страна. Поддържаната височина разделя триъгълника на две правоъгълни. Това е необходимо за доказателство.
Страната ще бъде разделена на два сегмента: x, y. Те трябва да бъдат изразени в известни термини. Частта, която се оказва в триъгълник с хипотенуза, равна на, ще бъде изразена чрез писане:
x = in * cos A.
Другият ще бъде равен на тази разлика:
y = s - в * cos A.
Сега трябва да напишем Питагоровата теорема за двете прави триъгълници на непозната височина. Тези формули ще изглеждат така:
n 2 = в 2 - (в * cos А) 2 ,
n 2 = a 2 - (c - c * cos A) 2 .
В тези равенства са идентични изрази отляво. Следователно, техните десни страни също ще бъдат равни. Лесно е да се пише. Сега трябва да отворите скобите:
в 2 - в 2 * (cos А) 2 = a 2 - с 2 + 2 с * в * cos А - в 2 * (cos А) 2 .
Ако извършим прехвърлянето и редукцията на такива термини, тогава получаваме първоначалната формула, която е написана след текста, т.е. косинусната теорема. Доказателството е завършено.
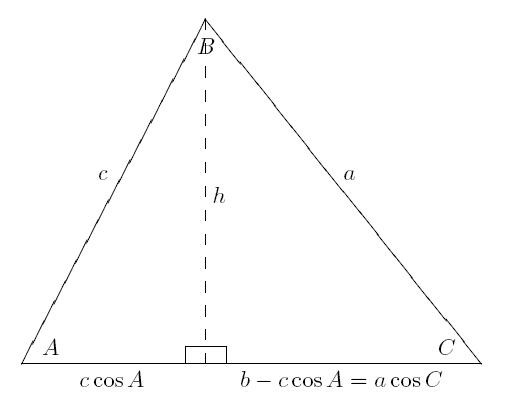
Доказателство на теоремата чрез вектори
Тя е много по-къса от предишната. И ако знаете свойствата на векторите, тогава косинусната теорема за триъгълника ще бъде доказана просто.
Ако страните a, b, c са обозначени съответно от векторите BC, AC и AB, тогава равноправието е вярно:
SU = AC - AB.
Сега трябва да извършите някои действия. Първият от тях е квадратът на двете страни на равенството:
BC 2 = AC 2 + AB 2 - 2 AC * AB.
Тогава равенството трябва да бъде пренаписано в скаларна форма, като се има предвид, че произведението на векторите е равно на косинуса на ъгъла между тях и техните скаларни стойности:
BC 2 = AC 2 + AB 2 - 2 AC * AB * cos A.
Остава само да се върнем към старата нотация и отново ще излезе косинусова теорема:
a 2 = 2 + s 2 - 2 * c * s * cos A.
Формули за други страни и всички ъгли
За да намерите страната, от косинусовата теорема трябва да извлечете квадратен корен. Формулата за квадратите на една от другите страни ще изглежда така:
с 2 = a 2 + до 2 - 2 * a * до * cos C.
За да напишете израза за квадрата на страната в , е необходимо да замените предишното равенство с от към, и обратно, и поставете ъгъла B под косинуса.
От основната формула на теоремата можем да изразим стойността на косинуса на ъгъла А:
cos А = (в 2 + с 2 - а 2 ) / (2 в * с).
Формули за други ъгли са получени по същия начин. Това е добра практика, така че можете да се опитате да ги напишете сами.
Естествено, няма нужда да се запомнят тези формули. Достатъчно е да се разбере теоремата и способността да се извлекат тези изрази от нейния основен запис.
Първоначалната формула на теоремата дава възможност да се намери страна, ако ъгълът не е между двата известни. Например, трябва да намерите в , когато са дадени стойностите: a, c, a . Или е неизвестно с , но има стойности a, b, a .
В тази ситуация трябва да преместите всички формули на допълнението наляво. Това равенство се получава:
с 2 - 2 * в * с * cos А + в 2 - а 2 = 0.
Препишете го в малко по-различна форма:
с 2 - (2 * в * cos А) * с + (в 2 - и 2 ) = 0.
Лесно можете да видите квадратичното уравнение. В него неизвестното количество е с и всички останали са дадени. Затова е достатъчно да се реши с помощта на дискриминант. Така че неизвестната страна ще бъде намерена.
По същия начин се получава формулата за втората страна:
2 - (2 * s * cos A) * c + (c 2 - a 2 ) = 0.
От други изрази тези формули също са лесни за получаване.
Как да изчислим ъгъла, без да изчисляваме косинуса?
Ако погледнете отблизо формулата на косинусовия ъгъл, получена по-рано, ще забележите следното:
- знаменателят на една фракция винаги е положително число, защото съдържа произведението на страни, които не могат да бъдат отрицателни;
- ъгълът ще зависи от знака на числителя.
Ъгъл А ще бъде:
- остра в ситуация, когато числителят е по-голям от нула;
- тъп, ако този израз е отрицателен;
- директно, когато е нула.
Между другото, последната ситуация превръща косинусната теорема в Питагоровата теорема. Защото при ъгъл от 90 ° косинусът му е нула, а последният изчезва.
Първа задача
състояние
Тъпият ъгъл на някой произволен триъгълник е 120º. За страните, за които е ограничен, е известно, че един от тях е с 8 см по-дълъг от другия, дължината на третата страна е 28 см. Необходимо е да се намери периметъра на триъгълника.
решение
Първо трябва да посочите една от страните с буквата “x”. В този случай другият ще бъде равен на (x + 8). Тъй като има изрази за трите страни, можете да използвате формулата, която дава косинусната теорема:
28 2 = (x + 8) 2 + x 2 - 2 * (x + 8) * x * cos 120º.
В таблиците за косинуси трябва да намерите стойност, съответстваща на 120 градуса. Това ще бъде числото 0.5 със знак минус. Сега е необходимо да отворите скобите, спазвайки всички правила и дайте подобни термини:
784 = x 2 + 16x + 64 + x 2 - 2x * (-0.5) * (x + 8);
784 = 2x2 + 16x + 64 + х2 + 8х;
3x 2 + 24x - 720 = 0.
Това квадратично уравнение се решава чрез намиране на дискриминант, който ще бъде равен на:
D = 24 2 - 4 * 3 * (- 720) = 9216.
Тъй като стойността му е по-голяма от нула, уравнението има два основни отговора.
x 1 = ((-24) + √ (9216)) / (2 * 3) = 12;
x 2 = ((-24) - √ (9216)) / (2 * 3) = -20.
Последният корен не може да бъде отговорът на проблема, защото партията трябва задължително да бъде положителна.
Така че двете страни са известни. Лесен за намиране на третия: 12 + 8 = 20 (cm). Сега можете да отговорите на въпроса за проблема. Периметър на триъгълник се определя като сума от всички страни:
24 + 12 + 20 = 60 (cm).
Отговор : периметърът е 60 сантиметра.

Проблем номер 2
състояние
В триъгълника са известни: c , равно на 2 cm; a , което е 10 cm; ъгъл C стойност от 120º. Изисква се да намериш страна.
решение
Първо трябва да използвате косинусната теорема и да извлечете формулата квадратично уравнение в която стойността в ще бъде неизвестна:
с 2 = a 2 + в 2 - 2 * a * в * cos C
и
в 2 - (2 * a * cos C) * в + (a 2 - c 2 ) = 0.
Необходимо е да се заменят всички известни стойности в условието:
в 2 - (2 * 10 * cos 120º) * в + (10 2 - 2 2 ) = 0.
Сега трябва да преброим това, което е възможно, за да опростим израза:
в 2 - (20 * (-1/2)) * в + (100 - 4) = 0
или
при 2 + 10 * в - 96 = 0.
Това е стандартно квадратично уравнение, което трябва да бъде решено чрез намиране на дискриминант:
D = (10) 2 - 4 * 1 * (-96) = 484.
Според формулите трябва да направите изчисления за неизвестната страна:
при 1 = (- 10 + 22) / 2 = 6 (cm);
в 2 = (- 10 - 22) / 2 = - 16 - този корен не удовлетворява решението на проблема, защото страната не може да бъде отрицателна.
Отговор: неизвестната страна е 6 cm.
Трета задача
състояние
В някой триъгълник са дадени страните: a, b, c , които са съответно 6 cm, 10 cm и 8 cm.
решение
Отново трябва да използвате косинусова теорема. Използва се нейният запис, в който има косинус на ъгъла А, тъй като точно това трябва да се изчисли. Ето формулата за косинуса на неизвестен ъгъл:
cos А = (в 2 + с 2 - а 2 ) / (2 в * с).
Остава да се заменят стойностите на страните и да се извършат всички изчисления:
cos A = (10 2 + 8 2 - 6 2 ) / (2 * 8 * 10).
След като всички термини се изравнят и се умножат числата от знаменателя:
cos A = (100 + 64 - 36) / (160).
След добавяне и разделяне се оказва:
cos A = 128/160 = 0.8.
Сега трябва да използвате таблицата на Bradis, за да разберете какъв ъгъл А. е. Най-близката стойност на ъгъла за този косинус е 36º54´.
Отговор: стойността на ъгъла А е 36º54´.