Примери за изчисляване на площта на цилиндъра

Има голям брой задачи, свързани с цилиндъра. Те трябва да намерят радиуса и височината на тялото или вида на напречното му сечение. Плюс това, понякога трябва да изчислите площта на цилиндъра и неговия обем.

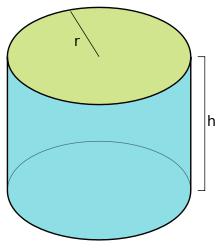
Кое тяло е цилиндър?

В хода на учебната програма се изучава кръгообразно, т.е. като такъв в основата, цилиндъра. Но има и елиптичен поглед на тази фигура. От заглавието е ясно, че неговата база ще бъде елипса или овал.

Има две цилиндрични бази. Те са еднакви и са свързани чрез сегменти, които съчетават съответните точки на основите. Те се наричат ​​цилиндрични генератори. Всички генератори са успоредни една на друга и равни. Те съставляват страничната повърхност на тялото.

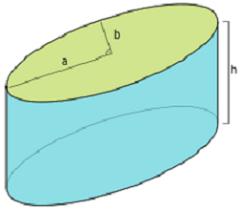
Като цяло, цилиндърът е наклонено тяло. Ако генераторите образуват прав ъгъл с основите, те вече говорят за права фигура.

Интересно е, че кръговият цилиндър е въртящо се тяло. Получава се чрез завъртане на правоъгълника около едната му страна.

Основните елементи на цилиндъра

Основните елементи на цилиндъра са следните.

1. Височина. Това е най-късото разстояние между основите на цилиндъра. Ако е права, то височината съвпада с образуващата.
2. Radius. Съвпада с това, което може да се проведе в основата.
3. Ос. Това е права линия, която съдържа центровете на двете бази. Оста е винаги успоредна на всички генератори. В правия цилиндър тя е перпендикулярна на основите.
4. Аксиална секция. Тя се формира при пресичането на цилиндъра от равнината, съдържаща оста.
5. Допирателна равнина. Той преминава през един от генераторите и е перпендикулярно на аксиалния разрез, който се изтегля през този генератор.

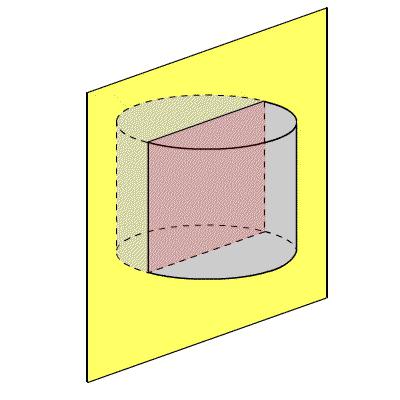
Как е свързан цилиндъра с призмата, вписана в нея или описана близо до нея?

Понякога има задачи, при които е необходимо да се изчисли площта на цилиндъра, докато някои елементи на свързаната призма са известни. Как се свързват тези цифри?

Ако призмата е вписана в цилиндър, тогава основите му са равни полигони. И те са вписани в съответната основа на цилиндъра. Страничните ръбове на призмата съвпадат с генераторите.

При описаната призма в основите има правилни полигони. Те са описани около цилиндровите кръгове, които са негови основи. Плоскостите, които съдържат лица на призмата, докосват цилиндъра по дължината на генераторите.

На площта на страничната повърхност и основата за прав кръгъл цилиндър

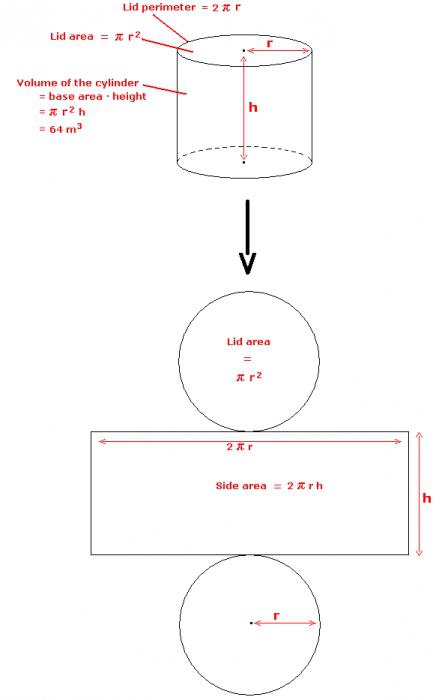
Ако сканирате страничната повърхност, ще получите правоъгълник. Страните му ще съвпадат с генератора и обиколка база. Следователно, страничната площ на цилиндъра ще бъде равна на произведението на тези две величини. Ако напишете формулата, получавате следното:

S _side = l * n,

където n е генераторът, l е дължината на окръжността.

И последният параметър се изчислява по формулата:

l = 2 π * r,

тук r е радиусът на окръжността, π е числото "pi", равно на 3.14.

Тъй като основата е кръг, нейната площ се изчислява, като се използва следният израз:

S _{първична} = π * r ² .

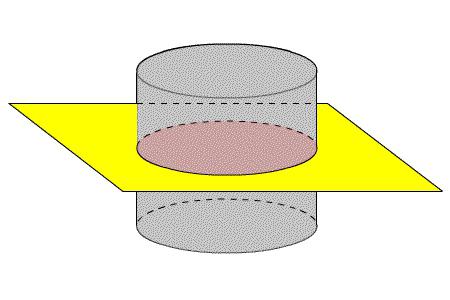
На площта на цялата повърхност на прав кръгъл цилиндър

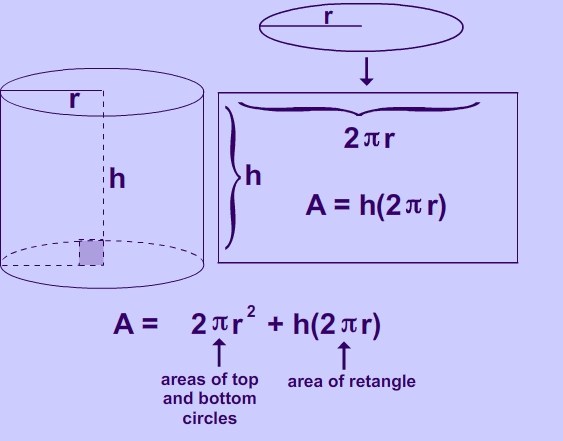
Тъй като тя се формира от две основи и странична повърхност, тези три количества трябва да бъдат добавени. Това означава, че общата площ на бутилката ще бъде изчислена по формулата:

S _етаж = 2 π * r * n + 2 π * r ² .

Често се пише в друга форма:

S _етаж = 2 π * r (n + r).

На областите на наклонен кръгов цилиндър

Що се отнася до основанията, тогава всички формули са едни и същи там, защото те са все още кръгове. Но страничната повърхност не дава правоъгълник.

За изчисляване на страничната повърхност на наклонения цилиндър е необходимо да се умножат стойностите на генератора и периметъра на участъка, който ще бъде перпендикулярно на избрания генератор.

Формулата изглежда така:

S _side = x * P,

където x - дължината на цилиндъра на генератора, P - периметъра на участъка.

Разделът, между другото, е по-добре да се избере така, че да образува елипса. Тогава ще бъдат опростени изчисленията на неговия периметър. Дължината на елипсата се изчислява по формулата, която дава приблизителен отговор. Но това често е достатъчно за училищните задачи:

l = π * (a + c),

където "а" и "б" са полуосите на елипсата, т.е. разстоянието от центъра до най-близките и най-отдалечените точки.

Площта на цялата повърхност трябва да се изчисли, като се използва следният израз:

S _етаж = 2 π * r ² + x * R.

Какви са някои участъци от прав кръгъл цилиндър?

Когато една секция минава през ос, нейната площ се определя като произведение на генератора и диаметъра на основата. Това се дължи на факта, че има формата на правоъгълник, чиито страни съвпадат с посочените елементи.

За да се намери площта на напречното сечение на цилиндър, който е успореден на аксиалния, също се нуждаем от формула за правоъгълник. В тази ситуация едната страна все още ще съвпада с височината, а другата е равна на хордата на основата. Последното съвпада с линията на профила по протежение на основата.

Когато секцията е перпендикулярна на оста, тя има формата на кръг. Освен това, неговата площ е същата като в основата на фигурата.

Може би дори пресичането под някакъв ъгъл спрямо оста. След това в напречното сечение се получава овал или част от него.

Примери за задачи

Задача номер 1. Даден е прав цилиндър, чиято основна площ е 12,56 cm2. Необходимо е да се изчисли общата площ на цилиндъра, ако височината му е 3 cm.

Решението. Необходимо е да се използва формулата за пълната площ на кръговия прави цилиндър. Но липсват данни, а именно радиусът на основата. Но районът на кръга е известен. От него е лесно да се изчисли радиуса.

Той е равен на корен квадратен от коефициента, който се получава чрез разделяне на площта на основата с pi. След разделянето на 12.56 с 3.14 излиза 4. Корен квадратен от 4 е 2. Следователно радиусът ще има точно тази стойност.

Сега можете да изчислите площта на страничната повърхност. За да направите това, умножете пи по радиус, височина и 2. Работата ще изглежда така: 3.14 * 3 * 2 * 2. Резултатът е: 37.68 cm ² .

За да преброите общата площ, трябва да добавите две бази (12.56 cm ² ) и странична повърхност (37.68 cm ² ). Резултатът е числото 50.24 cm2.

Отговор: S _пол = 50.24 cm ² .

Задача номер 2. Цилиндър с радиус 5 cm се потиска от равнина, успоредна на оста. Разстоянието от участъка до оста е 3 см. Височината на цилиндъра е 4 см. Необходимо е да се намери площта на участъка.

Решението. Формата на профила е правоъгълна. Едната му страна съвпада с височината на цилиндъра, а другата е равна на хордата. Ако първата стойност е известна, тогава трябва да се намери второто.

За да направите това, направете допълнителна конструкция. В основата си правим два сегмента. И двете ще започнат в центъра на кръга. Първият ще завърши в центъра на хордата и ще бъде равен на известното разстояние до оста. Вторият е в края на акорда.

успявам правоъгълен триъгълник. Известна е хипотенуза и един от краката. Хипотенузата съвпада с радиуса. Вторият крак е половината от акорда. Непознат крак, умножен по 2, ще даде желаната дължина на хордата. Изчисляваме стойността му.

За да намериш неизвестен крак, трябва да изравниш хипотенузата и познатия крак, да извадиш втория от първия и да вземеш квадратен корен. Квадратите са 25 и 9. Разликата им е 16. След екстракция квадратен корен 4. Това е желаният крак.

Акордът ще бъде равен на 4 * 2 = 8 (cm). Сега можете да изчислите площта на напречното сечение: 8 * 4 = 32 (cm ² ).

Отговор: S _Sich е 32 cm ² .

Задача номер 3. Необходимо е да се изчисли аксиалното сечение на цилиндъра. Известно е, че в него е вписан куб с ръб от 10 cm.

Решението. Аксиалната част на цилиндъра съвпада с правоъгълник, който преминава през четирите върха на куба и съдържа диагоналите на неговите бази. Страната на куба е генератор на цилиндъра, а диагоналът на основата съвпада с диаметъра. Продуктът от тези две количества дава площта, която трябва да бъде призната в проблема.

За да намерим диаметъра, трябва да използваме знанието, че в основата на куба има квадрат, а диагоналът му образува равностранен правоъгълен триъгълник. Неговата хипотенуза е желаната диагонална форма.

За да го изчислим, се нуждаете от формулата на Питагоровата теорема. Необходимо е да се закръгли страната на куба, да се умножи по 2 и да се извлече квадратният корен. Десет до втора степен е сто. Умножено по 2 - двеста. Квадратният корен от 200 е 10√2.

Разделът отново е правоъгълник със страни 10 и 10√2. Неговата площ е лесна за преброяване чрез умножаване на тези стойности.

Отговорът е. S сечение = 100 × ² cm2.