Какъв е коефициентът на пречупване на стъклото? И кога е необходимо да се знае?

Когато се решават проблеми в оптиката, често се изисква да се знае коефициента на пречупване на стъкло, вода или друго вещество. И в различни ситуации могат да бъдат включени както абсолютни, така и относителни стойности на тази стойност.

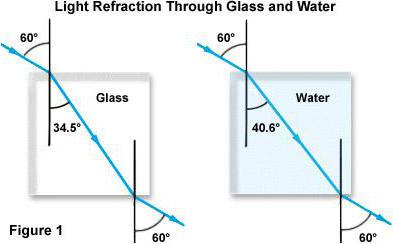
Два вида рефракционен индекс

Първо, фактът, че този брой показва: как тази или онази прозрачна среда променя посоката на разпространение на светлината. и електромагнитна вълна може да идва от вакуум, а след това индексът на пречупване на стъкло или друго вещество ще се нарича абсолютен. В повечето случаи стойността му е в диапазона от 1 до 2. Само в много редки случаи рефракционният индекс е по-голям от два.

Ако пред субекта има по-плътна среда от вакуума, те вече говорят за относителна стойност. И се изчислява като съотношение на две абсолютни стойности. Например, роднина индекс на пречупване Водното стъкло ще бъде равно на конкретните абсолютни стойности за стъкло и вода.

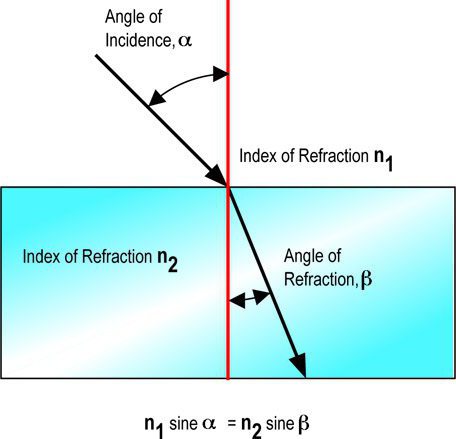
Във всеки случай, тя се обозначава с латинската буква "en" - n. Тази стойност се получава чрез разделяне на една и съща стойност, следователно, това е просто коефициент, който няма име.

Каква формула може да се използва за изчисляване на индекса на рефракция?

Ако приемем ъгъла на падане като "алфа", а ъгълът на пречупване е означен като "бета", тогава формулата за абсолютната стойност на рефракционния индекс изглежда така: n = sin α / sin β. В литературата на английски език често можете да намерите друго наименование. Когато ъгълът на падане е i, и пречупването е r.

Има и друга формула за изчисляване на коефициента на пречупване на светлината в стъкло и други прозрачни среди. Тя е свързана със скоростта на светлината във вакуум и от нея, но вече в разглежданата субстанция.

Тогава изглежда така: n = c / νλ. Тук c е скоростта на светлината във вакуум, ν е нейната скорост в прозрачна среда, а λ е дължината на вълната.

Какво определя индекса на рефракция?

Тя се определя от скоростта, с която светлината пътува в разглежданата среда. Въздухът в това отношение е много близо до вакуума, следователно светлинните вълни в него се разпространяват практически не се отклоняват от първоначалната си посока. Следователно, ако се определи коефициентът на пречупване на стъклен въздух или друго вещество, граничещо с въздуха, последният обикновено се приема за вакуум.

Всяка друга среда има свои характеристики. Те имат различна плътност, имат своя собствена температура, както и еластични напрежения. Всичко това се отразява на рефракцията на светлината по материя.

Не последната роля в промяната на посоката на разпространение на вълната се играе от характеристиките на светлината. Бялата светлина се състои от различни цветове, от червено до виолетово. Всяка част от спектъра се пречупва по свой собствен начин. Освен това, стойността на индекса за вълната на червената част на спектъра винаги ще бъде по-малка от останалата. Например, показателят на пречупване на TF-1 стъкло варира от 1.6421 до 1.67298, съответно, от червената до виолетовата част на спектъра.

Примери за стойности за различни вещества

Тук са стойностите на абсолютните стойности, т.е. коефициентът на пречупване, когато лъчът преминава от вакуум (който е равен на въздуха) през друго вещество.

Тези цифри ще бъдат необходими, ако е необходимо да се определи коефициентът на пречупване на стъклото спрямо други среди.

Какви други стойности се използват при решаване на проблеми?

Пълно отражение. Наблюдава се, когато светлината преминава от по-плътна до по-плътна среда. Тук, при определен ъгъл на падане, пречупването се извършва под прав ъгъл. Тоест, лъчът се плъзга по границата на две среди.

Максималният ъгъл на общото отражение е неговата минимална стойност, при която светлината не влиза в по-малко плътна среда. По-малко от него - пречупването се случва, и още - отражение в същата среда, от която светлината се движи.

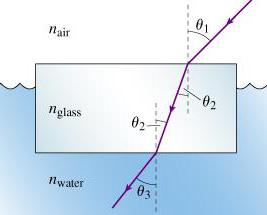
Проблем номер 1

Състояние. Коефициентът на пречупване на стъклото е 1.52. Необходимо е да се определи ограничителният ъгъл, до който светлината напълно се отразява от отделянето на повърхностите: стъкло с въздух, вода с въздух, стъкло с вода.

Решението.

Ще трябва да използвате тези показатели за пречупване на водата, дадени в таблицата. Той е за въздух, който е равен на един.

Решението и в трите случая се свежда до изчисленията по формулата:

sin α ₀ / sin β = n ₁ / n ₂ , където n _{2 се} отнася до средата, от която се разпространява светлината, и n ₁ където прониква.

Буквата α ₀ означава граничния ъгъл. Стойността на ъгъла β е 90 градуса. Това означава, че синусът му ще бъде един.

За първия случай: sin α ₀ = 1 / n _стъкло , тогава граничният ъгъл е равен на arcsine на 1 / n _стъкло . 1 / 1.52 = 0.6579. Ъгълът е 41.14º.

Във втория случай при определяне на аркината е необходимо да се замени стойността на индекса на пречупване на водата. Фракцията 1 / n _вода ще приеме стойността 1 / 1.33 = 0, 7519. Това е ъгълът arcsine от 48.75º.

Третият случай е описан от съотношението n на _водата и n на _{стъклото} . Arcsine ще трябва да изчисли за частта: 1.33 / 1.52, т.е. числото 0.875. Намерете стойността на ограничаващия ъгъл по нейната дъга: 61.05º.

Отговор: 41.14 º, 48.75 º, 61.05 º.

Проблем номер 2

Състояние. Стъклена призма се потапя в съд с вода. Нейният индекс на пречупване е 1.5. Призмата е базирана правоъгълен триъгълник. По-големият крак е перпендикулярно на дъното, а вторият е успореден на него. Светлинният лъч пада нормално върху горната повърхност на призмата. Какъв трябва да бъде най-малкият ъгъл между хоризонталния крак и хипотенузата, за да може светлината да достигне до крака, който е перпендикулярно на дъното на съда и да излезе от призмата?

Решението.

За да може лъчът да излезе от призмата по описания начин, той трябва да падне под краен ъгъл по вътрешния ръб (този, който е хипотенуза на триъгълника в участъка на призмата). Този граничен ъгъл се оказва равен на желания ъгъл на правоъгълен триъгълник. От закона за пречупване на светлината се оказва, че синусът на ограничителния ъгъл, разделен от синуса на 90 градуса, е равен на съотношението на два показателя на пречупване: вода към стъкло.

Изчисленията водят до тази стойност за граничния ъгъл: 62 ° 30.

Отговорът: 62º30´.