Какво е конус в геометрията? Дефиниция, формули, примерна задача

Познаването на свойствата на геометричните фигури позволява не само да се решават теоретични проблеми, но и да се извършват различни практически изчисления. Една от тези фигури, чиито свойства ще бъдат разгледани в тази статия, е конус. Какво е конус, какъв вид е той, как да се намери неговата площ и обем? Всички тези въпроси са подчертани подробно по-долу.

Обща дефиниция на конус в геометрията

Стереометрията, която изучава характеристиките на фигурите в триизмерното пространство, дава следния отговор на въпроса какво представлява конусът: това е фигура, чиято повърхност се формира от набор от прави линии, които свързват определена точка в пространството с определена крива в равнината.

Маркираната точка на пространството се нарича върхът на конуса, а правите сегменти са генериранията на фигурата или нейните генератори, а самата крива в равнината е directrix.

Според горната дефиниция е подходящ цял клас фигури, най-известните от които са кръгли, елиптични, параболични и хиперболични конуси. Елиптичната фигура е показана по-долу.

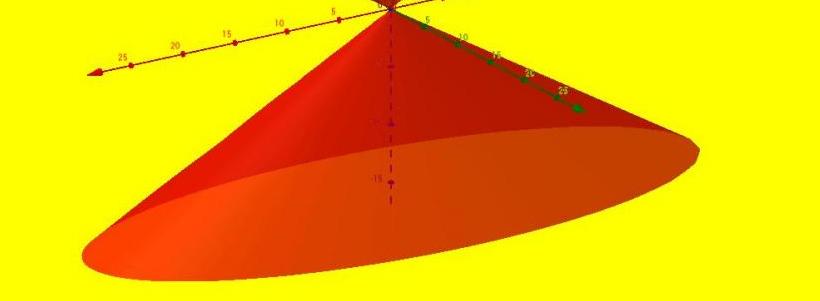
Дирекцията на този конус е затворена елипса, която ограничава основата на фигурата. Генераторите на всеки конус заедно образуват конична повърхност, която се нарича странична. Тези две повърхности (основата и страната) ограничават пространствения обем, който обикновено се нарича обем на конуса.

Кръгла права конус - фигура на въртене

Елиптичният конус, показан на фигурата по-горе, не може да се получи като резултат от въртенето на плоска фигура. Единственият представител на класа конуси, който може да се формира чрез въртене, е кръгъл прав конус. Тази цифра е показана по-долу.

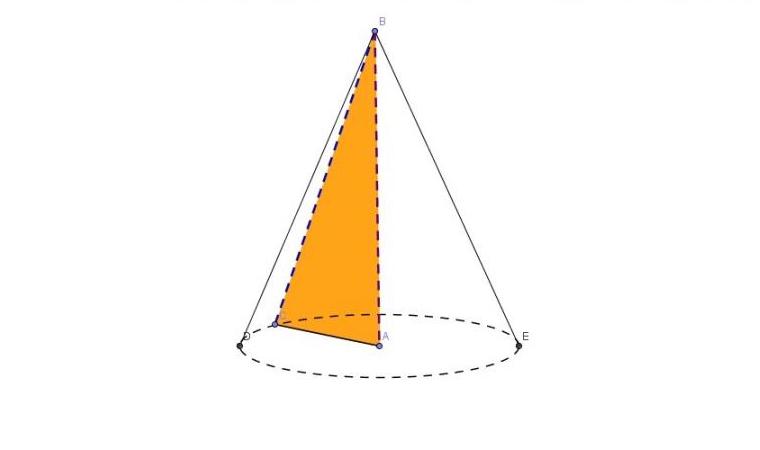
Вижда се, че неговата основа представлява идеален кръг. Освен това, всяка част от страничната повърхност с равнина, успоредна на основата, също ще бъде кръг, но с по-малък диаметър от фигурата в основата.

Оранжевият триъгълник ABC, избран в конуса, е правоъгълен. Може да се види, че кракът АС е основен радиус r. Кракът AB е височината на фигурата h. По конструкция е ясно, че височината е дължината на перпендикуляра, изтеглена от върха на фигурата В до равнината на основата (окръжност). Тази височина пресича кръга в центъра му. Последното означава, че конусът е прав. И накрая, хипотенузата на триъгълника BC не е нищо повече от конусообразна генерация.

За да се образува конус, използвайки описания триъгълник, е необходимо да го завъртите около страната AB.

За визуално представяне на разликата между правите и наклонените конуси представяме съответната фигура.

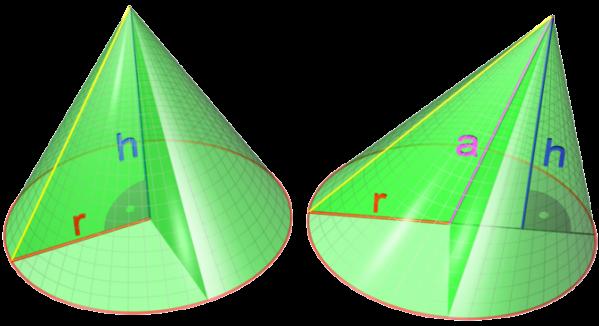
Разликата между двете фигури е очевидна: ако основите им са едни и същи, тогава височините, спуснати от върха, пресичат основите в различни точки. Първата фигура е права, втората е наклонена.

Линейни параметри на кръгъл прав конус и ъгъл в основата

Тези параметри вече са посочени по-горе. Избройте ги отново:

• радиус r;
• височина h;
• генератор g.

За да определите еднозначно един конус, тези три параметъра са излишни, т.е. въпросната цифра може да бъде конструирана и всички нейни свойства могат да бъдат изчислени, знаейки само два от трите посочени параметъра. Въз основа на разглежданата схема за получаване на конус чрез завъртане на правоъгълен триъгълник, можем да напишем следната връзка между генератора, радиуса и височината на конуса:

g = √ (r² + h²).

Това равенство е очевидно и не изисква доказателство (помнете теоремата на Питагор).

Можете да зададете конус не само с помощта на правите сегменти r, h и g, но също и с помощта на ъгловата мярка между някой от генераторите на форми и базовата равнина. Обозначете този ъгъл с буквата φ. Използвайки дефиницията на тригонометричните функции, можем да напишем поредица от формули, в които ъгълът φ свързва линейните параметри. Пишем основните:

g = h / sin (φ);

g = r / cos (φ);

h = r * tg (φ).

Площта на повърхността на фигурата

Като се има предвид въпросът какво представлява конусът, представяме формула за определяне на площта на нейната пълна повърхност. За да стане по-ясно, какво ще се обсъжда, ние ще приведем сканирането в равнината на въпросната фигура.

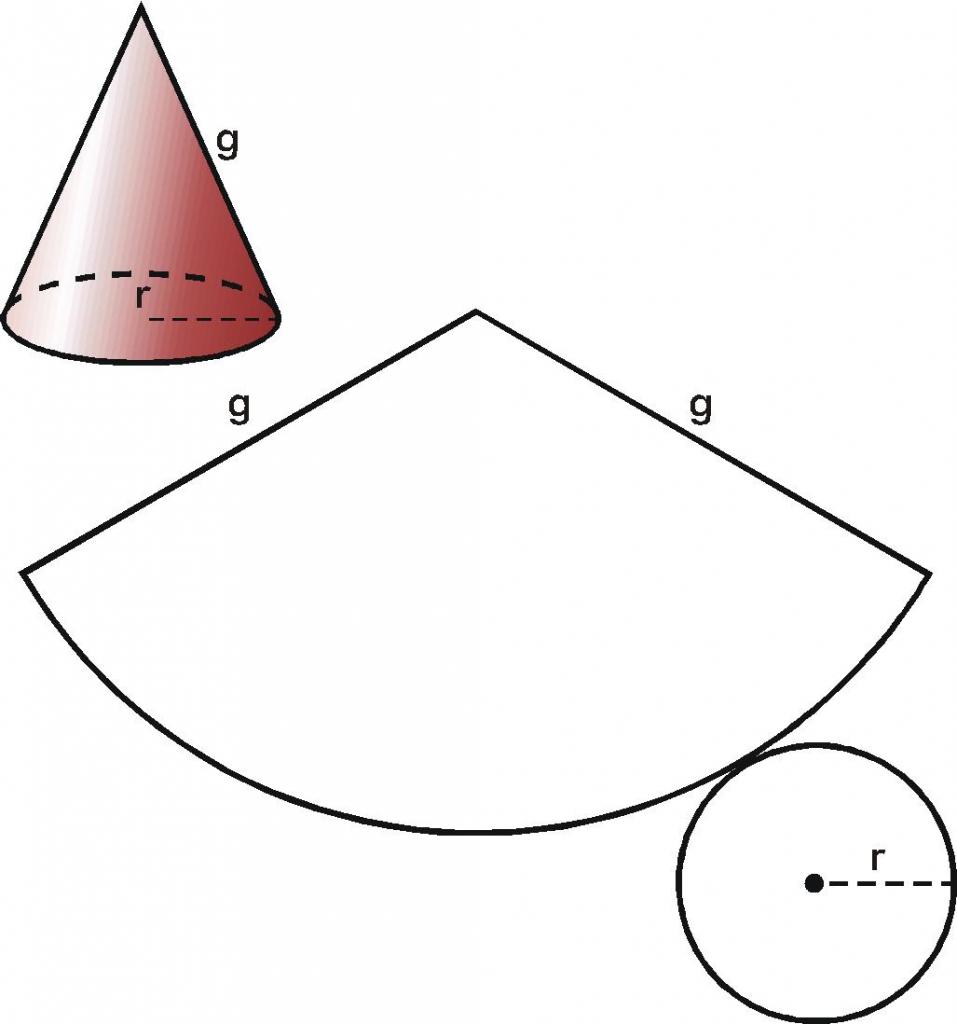
Развитието на конус в равнината се състои от две фигури. Кръгът е основата на конуса, кръговият сектор с радиус g е страничната повърхност. Кръгъл сектор е лесно да се получи, ако вземете конична повърхност на хартията и я отрежете по всяка образуваща g. Разширявайки тази повърхност, получаваме желания сектор.

Определянето на площта _на окръжността не е проблем. Съответният израз е показан по-долу:

S _o = pi * r².

Що се отнася до кръговия сектор, неговите необходими параметри за изчисляване на площта S _b също _са известни: радиусът g и дължината на дъгата, съответстващи на обиколката на разглеждания по-горе кръг. Формулата за изчисляване на площта на страничната повърхност на конуса S _b е:

S _b = pi * r * g.

Така общата площ на фигурата е равна на:

S = S _o + S _b = pi * r * (r + g).

Формула за обем

Знаейки какво е конус правоъгълник, лесно е да напишем формулата за нейния обем. Тъй като въпросната цифра може да се счита за пирамида с безкраен брой странични ръбове, то за нея, както и за всяка пирамида, обемът може да се изчисли по формулата:

V = 1/3 * S _o * h.

Стойността на квадрата S _o вече е дадена по-горе, следователно, необходимата формула за обема на прав конус с кръгла основа ще бъде следната:

V = 1/3 * pi * r² * h.

Решаване на геометричен проблем

Известно е, че стойността на повърхността на конуса на кръглата права е 300 cm². Необходимо е да се определи радиусът на конуса, като се знае, че неговата образуваща е 15 cm.

Записваме равенство за площта и заместваме стойността g = 15 cm и S = ​​300 cm², получаваме:

S = pi * r * (r + g) =>

300 = pi * r² + 15 * pi * r.

Разделете лявата и дясната страна на числото pi, получаваме следното квадратично уравнение:

r² + 15 * r - 95.54 = 0.

Решаваме това уравнение чрез дискриминанта, получаваме:

D = 15² - 4 * (- 95.54) = 607.16;

r = (-15 ± )D) / 2 = (4.82; -19.82).

Отрицателен корен не отговаря на условието на проблема, така че можете да напишете отговора: дадения конус има радиус от 4,82 cm.