Тригонометрия от нулата: основни понятия, история

Синус, косинус, допирателна - когато произнасяте тези думи в присъствието на ученици от средните училища, можете да сте сигурни, че две трети от тях ще загубят интерес към по-нататъшен разговор. Причината е, че основите на тригонометрията в училище се преподават в пълна изолация от реалността и затова учениците не виждат смисъл в изучаването на формули и теореми.

Всъщност, при по-внимателно разглеждане, тази област на знанието се оказва доста интересна, както и приложна - тригонометрията намира приложение в астрономията, строителството, физиката, музиката и много други области.

Нека се запознаем с основните понятия и ще назовем няколко причини за изучаване на тази част от математическата наука.

История на

Не е известно в кой момент човечеството е започнало да създава бъдеща тригонометрия от нулата. Документирано е обаче, че още през второто хилядолетие преди Христа египтяните са били запознати с основите на тази наука: археолозите са намерили папирус със задача, в която е необходимо да се намери ъгълът на наклона на пирамидата на две познати страни.

По-сериозен успех постигнаха учени от Древен Вавилон. През вековете, които правят астрономия, те овладяват редица теореми, въвеждат специални начини за измерване на ъгли, които, между другото, използваме днес: градуси, минути и секунди са заети от европейската наука в гръко-римската култура, в която тези единици идват от вавилонците.

Предполага се, че известната питагорова теорема, свързана с основите на тригонометрията, е била известна на вавилонците преди почти четири хиляди години.

име

Буквално терминът "тригонометрия" може да се преведе като "измерващ триъгълник". Основният предмет на изследване в тази секция на науката в продължение на много векове беше правоъгълен триъгълник или по-скоро, връзката между величините на ъглите и дължините на нейните страни (днес изследването на тригонометрията от нулата започва с този раздел). Често съществуват ситуации в живота, когато е невъзможно да се измери на практика всички необходими параметри на даден обект (или разстояние до обект), а след това става необходимо да се получат липсващите данни чрез изчисления.

Например, в миналото човек не можеше да измери разстоянието до космически обекти но опитите за изчисляване на тези разстояния се случват много преди появата на нашата ера. Тригонометрията също играе важна роля в навигацията: с известни познания капитанът винаги може да се движи през нощта от звездите и да коригира курса.

Основни понятия

За да овладеете тригонометрията от нулата, трябва да разберете и запомните няколко основни термина.

Синусът на определен ъгъл е съотношението на противоположния крак към хипотенузата. Изясняваме, че противоположният крак е страната, противоположна на ъгъла, който разглеждаме. Така, ако ъгълът е 30 градуса, синусът на този ъгъл винаги ще бъде за всеки размер на триъгълника ½. Косинусът на ъгъла е съотношението на съседния крак към хипотенузата.

Допирателната е съотношението на противоположния крак към съседния (или, съответно, съотношението на синус към косинус). Котангенсът е единица, разделена на допирателна.

Заслужава да се спомене известният Пи (3.14 ...), който представлява половината обиколка с радиус от една единица.

Популярни бъгове

Хората, които изучават тригонометрията от нулата, правят серия от грешки - най-вече от небрежност.

Първо, при решаването на проблеми в геометрията трябва да се помни, че използването на синуси и косинуси е възможно само в правоъгълен триъгълник. Случва се, че студент „на машината” поема най-дългата страна на триъгълника за хипотенузата и получава неверни резултати от изчисленията.

Второ, на първо място е лесно да се обърка стойностите на синуса и косинуса за избрания ъгъл: напомняме, че синусът от 30 градуса е числено равен на косинуса от 60 и обратно. При подмяна на грешен номер всички по-нататъшни изчисления ще бъдат погрешни.

Трето, докато проблемът не бъде напълно решен, не трябва да се закръгляват никакви стойности, да се извличат корените, да се записва една обикновена част като десетична. Често учениците се стремят да получат „красив” номер в задачата на тригонометрията и незабавно да извлекат корена от три, макар че с точно едно действие този корен може да бъде намален.

Етимология на думата "синус"

Историята на думата "синус" е наистина необичайна. Факт е, че буквалният превод на тази дума от латински означава "куха". Това е така, защото правилното разбиране на думата се губи при превода от един език на друг.

Имената на основните тригонометрични функции произхождат от Индия, където понятието за синус се обозначава с думата "тетиво" на санскрит - фактът, че сегментът заедно с дъгата на окръжност, на която се основава, прилича на лък. По време на разцвета на арабската цивилизация индийските постижения в областта на тригонометрията са заимствани и терминът е прехвърлен на арабски език под формата на транскрипция. Случило се така, че на този език вече имаше подобна дума, означаваща кухина, и ако арабите разбраха фонетичната разлика между местната и заимствана дума, тогава европейците, превеждайки научните трактати на латински, буквално преведоха арабската дума, която нямаше нищо общо с концепцията за синусите. , Ние ги използваме и до днес.

Таблици със стойности

Има таблици, в които са въведени числени стойности за синусите, косинусите и тангентите на всички възможни ъгли. По-долу представяме данните за ъгли от 0, 30, 45, 60 и 90 градуса, които трябва да се научат като задължителен раздел на тригонометрията за манекените, ползата от запомнянето им е доста лесна.

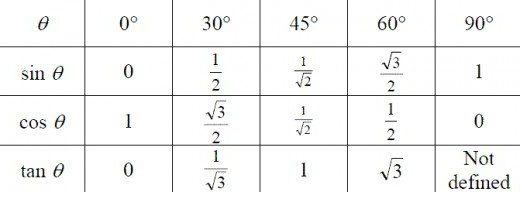Ако се случи, че цифровата стойност на синуса или косинуса на ъгъла "излетя от главата", има начин да го извлечете сами.

Геометрично представяне

Начертайте кръг, през центъра му нарисуваме абсцисата и ординатните оси. Оста на абсцисата се намира хоризонтално, ординатната ос е вертикална. Обикновено те са подписани съответно като “X” и “Y”. Сега от центъра на окръжността нарисуваме линия по такъв начин, че да се получи ъгълът, от който се нуждаем между нея и оста Х. Накрая, от точката, където линията пресича кръга, ние спускаме перпендикуляра към оста Х. Дължината на получения сегмент ще бъде равна на числената стойност на синуса на нашия ъгъл.

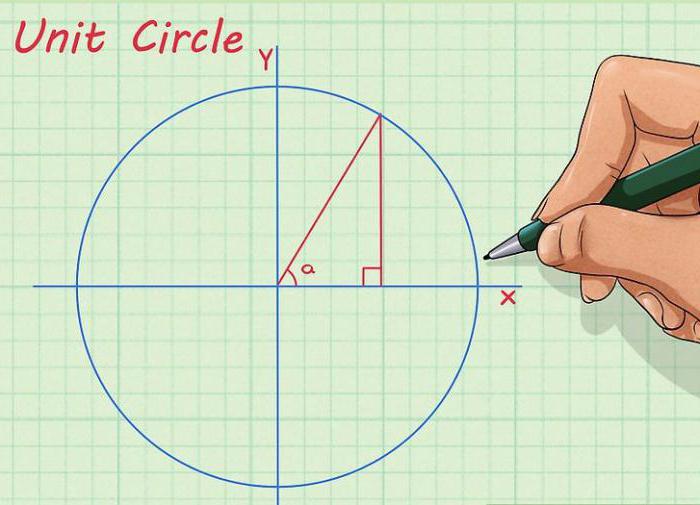Този метод е много уместен, ако сте забравили желаната стойност, например на изпита, и няма подготвен учебник за тригонометрията. Няма да получите точна цифра по този начин, но определено ще видите разликата между ½ и 1.73 / 2 (синус и косинус от 30 градусов ъгъл).

приложение

Един от първите специалисти, които са използвали тригонометрията, са моряците, които нямат друга отправна точка в открито море, освен небето над главите им. Днес капитаните на корабите (самолети и други) видове транспорт) Те не търсят най-краткия път през звездите, но активно прибягват до GPS навигация, което би било невъзможно без използването на тригонометрия.

В почти всеки физика Вие очаквате изчисления, използвайки синуси и косинуси: дали това е прилагане на сила в механиката, изчисления на пътя на обектите в кинематиката, осцилации, разпространение на вълните, пречупване на светлината - просто не може да се направи без основна тригонометрия във формули.

Друга професия, която е немислима без тригонометрия, е инспекторът. Използвайки теодолит и ниво или по-сложно устройство - тахиометър, тези хора измерват разликата във височината между различните точки на земната повърхност.

честота

Тригонометрията се занимава не само с ъгли и страни на триъгълника, въпреки че от този момент тя започва своето съществуване. Във всички области, където има цикличност (биология, медицина, физика, музика и т.н.), ще срещнете график, чието име вероятно знаете е синусоида.

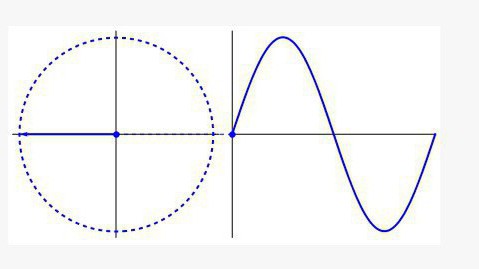Такава графика е кръг, развит по времевата ос и прилича на вълна. Ако някога сте работили с осцилоскоп в един клас по физика, разбирате за какво става въпрос. Както музикалния еквалайзер, така и устройството, показващо сърдечните ритми, използват тригонометричните формули в работата си.

В заключение

Мислейки за това как да научим тригонометрията, мнозинството от учениците от средните и висшите училища започват да го разглеждат като сложна и непрактична наука, тъй като те се запознават само с скучна информация от учебник.

По отношение на непрактичността - вече видяхме, че в различна степен способността да се обработват синусите и тангентите е необходима в почти всяка област на дейност. Що се отнася до сложността ... Помислете: ако хората са използвали това знание преди повече от две хиляди години, когато възрастен е имал по-малко знания от днешния гимназист, наистина ли е възможно да изучавате тази област на науката на основно ниво? Няколко часа внимателни уроци с решаване на проблеми - и ще постигнете целта си, като изучавате основния курс, т. Нар. Тригонометрия за манекени.