Трапецовидна област: формули и изчислителни методи

За да се чувствате уверено и успешно да решавате проблеми в уроците по геометрия, не е достатъчно да научите формули. Те трябва първо да разберат. Да се ​​страхуваш и още повече да мразиш формули, е непродуктивно. В тази статия, наличният език ще анализира различни начини за намиране на областта на трапец. За по-добро овладяване на съответните правила и теореми, ще обърнем внимание на неговите свойства. Това ще помогне да се разбере как работят правилата и в какви случаи трябва да се прилагат тези или тези формули.

Определете трапецоида

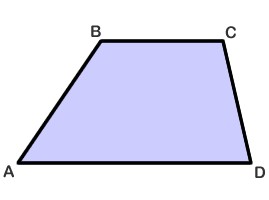Каква е тази цифра като цяло? Трапецоидът е полигон от четири ъгъла с две паралелни страни. Другите две страни на трапеца могат да бъдат наклонени под различни ъгли. Неговите паралелни страни се наричат ​​бази, а за не-паралелни страни се използва името "страни" или "бедра". Такива фигури са често срещани в ежедневието. Контурите на трапеца могат да се видят в силуетите на облеклото, интериора, мебелите, съдовете и много други. А трапецовидни могат да бъдат от различни видове: гъвкави, равностранни и правоъгълни. Повече подробности за техните видове и свойства ще бъдат разгледани по-късно в статията.

Трапецовидни свойства

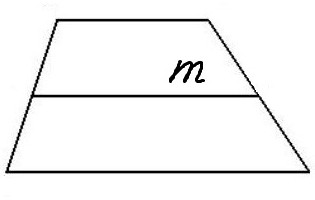Нека накратко обсъдим свойствата на тази фигура. Сумата на ъглите, съседни на всяка страна, е винаги 180 °. Трябва да се отбележи, че всички ъгли на трапецовида са на 360 °. Trapezium има концепцията за средната линия. Ако свържете средните точки на страните с сегмент, това ще бъде средната линия. Той е обозначен като m. Средната линия има важни свойства: тя винаги е успоредна на базите (ние помним, че базите са успоредни един на друг) и са равни на тяхната половин сума:

m = (a + b) / 2.

Тази дефиниция трябва да бъде научена и разбрана, защото тя е ключът към решаването на множество проблеми!

В трапецовидна форма винаги можете да намалите височината на основата. Височината е перпендикулярна, често обозначавана със символа h, който се изтегля от всяка точка на една база към друга база или нейното продължение. Средната линия и височината ще ви помогнат да намерите областта на трапеца. Тези задачи са най-често срещаните в курса по геометрия на училището и редовно се появяват сред тестовите и изпитни документи.

Най-простите формули на трапецовата област

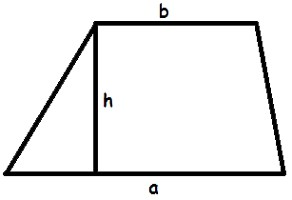Нека разгледаме двете най-популярни и прости формули, с помощта на които да намерим мястото на трапеца. Достатъчно е да умножите височината с половината от базите, за да намерите лесно желаното:

S = h * (a + b) / 2.

В тази формула а, б означаваме основата на трапеца, h - височина. За удобство на възприемането, в тази статия знаците за умножение се маркират със символа (*) във формулите, въпреки че в официалните справочници знакът за умножение обикновено се пропуска.

Помислете за пример.

Като се има предвид: трапец с две бази, равни на 10 и 14 см, височината е 7 см. Каква е площта на трапеца?

Нека анализираме решението на този проблем. Съгласно тази формула, първо трябва да намерим полу-сбор от бази: (10 + 14) / 2 = 12. Така полу-сумата е равна на 12 см. Сега умножаваме полу-сумата по височина: 12 * 7 = 84. Необходимото е намерено. Отговор: площта на трапеца е 84 квадратни метра. см.

Втората добре известна формула казва: площта на трапеца е равна на произведението на централната линия и височината на трапеца. Това е, всъщност, следва от предишната концепция за средната линия: S = m * h.

Използване на диагонали за изчисления

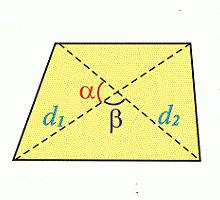
Друг начин за намиране на трапецовидната област всъщност не е толкова сложен. Той е свързан с неговите диагонали. Съгласно тази формула, за да се намери площта, е необходимо да се умножи полупродукта на диагоналите (d ₁ d ₂ ) със синуса на ъгъла между тях:

S = ½ d ₁ d ₂ sin a.

Помислете за задача, която показва прилагането на този метод. Даден е трапецовиден с диагонали съответно 8 и 13 см. Ъгълът а между диагоналите е 30 °. Намерете областта на трапеца.

Решението. Използвайки горната формула, е лесно да се изчисли необходимото. Както знаете, грях 30 ° е 0.5. Следователно, S = 8 * 13 * 0.5 = 52. Отговор: площта е 52 кв.м. см.

Търсим област на равностранен трапец.

Трапецоидът може да бъде равностранен (равнобедрен). Страните му са еднакви и ъглите в основите са еднакви, което е добре илюстрирано с чертежа. Равностранен трапец има същите свойства като обикновен, плюс редица специални. Кръг може да бъде описан около еднополярно трапецо, а в него може да бъде вписан кръг.

Какви са методите за изчисляване на площта на такава цифра? Следващият метод изисква големи изчисления. За да го използвате, трябва да знаете стойностите на синуса (sin) и косинуса (cos) на ъгъла в основата на трапеца. За да ги изчислите, са необходими таблици Bradis или инженерен калкулатор. Ето тази формула:

S = c * sin a * ( a - c * cos a ),

където c е страничното бедро, a е ъгълът на долната основа.

Равностранен трапец има диагонали със същата дължина. Обратното също е вярно: ако диагоналът е равен, то той е равнобедрен. Следователно следващата формула, която помага да се намери площта на трапеца, е полупродуктът на квадрата на диагоналите в синуса на ъгъла между тях: S = ½ d ² sin a.

Намерете областта на правоъгълния трапец

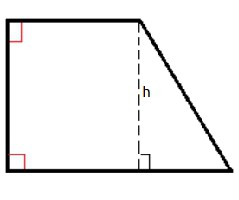
Известен специален случай правоъгълен трапец. Това е трапец, в който едната страна (нейното бедро) е в непосредствена близост до основите под прав ъгъл. Той има свойствата на обикновен трапец. Освен това има много интересна функция. Разликата на квадратите на диагоналите на такъв трапец е равна на разликата на квадратите на нейните бази. За целта те използват всички описани по-горе методи за изчисляване на площта.

Нанесете изобретателност

Има един трик, който може да помогне в случай на забравяне на специфични формули. Помислете внимателно какво е трапецовидно. Ако я разделим психически на части, ще станем познати и разбираеми геометрични фигури: квадрат или правоъгълник и триъгълник (един или два). Ако височината и страните на трапеца са известни, можете да използвате формулите триъгълна зона и правоъгълник, след което се съберат всички получени стойности.

Илюстрираме това със следния пример. Даден е правоъгълен трапец. Ъгъл С = 45 °, ъглите А, D са 90 °. Горната основа на трапецоида е 20 см, височината е 16 см. Необходимо е да се изчисли площта на фигурата.

решение

Тази фигура очевидно се състои от правоъгълник (ако двата ъгъла са 90 °) и триъгълник. Тъй като трапецът е правоъгълен, височината му е равна на неговата страна, т.е. 16 см. Имаме правоъгълник със страни 20 и 16 см, съответно. Разгледайте сега триъгълник, чийто ъгъл е 45 °. Знаем, че едната му страна е 16 см. Тъй като тази страна е едновременно височина на трапеца (и знаем, че височината пада под основа под прав ъгъл), затова вторият ъгъл на триъгълника е 90 °. Следователно оставащият ъгъл на триъгълника е 45 °. В резултат на това се получава правоъгълен равнобедрен триъгълник, чиито две страни са еднакви. Това означава, че другата страна на триъгълника е равна на височината, т.е. 16 см. Остава да се изчисли площта на триъгълника и правоъгълника и да се добавят получените стойности.

област правоъгълен триъгълник равна на половината от произведението на краката му: S = (16 * 16) / 2 = 128. Площта на правоъгълника е равна на произведението на нейната ширина по дължината: S = 20 * 16 = 320. Намерихме необходимото: площ на трапец S = 128 + 320 = 448 квадрат. Можете лесно да проверите отново, като използвате горните формули, отговорът ще бъде идентичен.

Използвайте формулата Pick

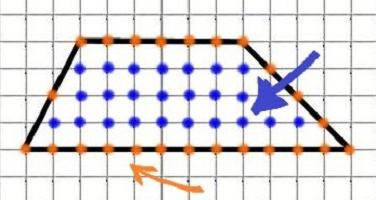
И накрая, представяме друга оригинална формула, която помага да се намери областта на трапец. Нарича се формулата Pick. Удобно е да се използва, когато трапецовидната лента е начертана на карирана хартия. Подобни задачи често се срещат в материалите на GIA. Изглежда така:

S = M / 2 + N - 1,

в тази формула М е броят на възлите, т.е. пресечната точка на линиите на фигурата с линиите на клетката на границите на трапецовида (оранжеви точки на фигурата), N е броят на възлите във фигурата (сини точки). Най-удобно е да го използвате, когато намирате областта на неправилен многоъгълник. Но колкото по-голям е арсеналът от използвани методи, толкова по-малко грешки и по-добри резултати.

Разбира се, дадената информация далеч не е изчерпана от видовете и свойствата на трапеца, както и от методите за търсене на нейната област. Тази статия предоставя преглед на най-важните му характеристики. При решаването на геометрични проблеми е важно да действаме постепенно, да започнем с лесни формули и задачи, последователно да консолидираме разбирането, да преминем към друго ниво на сложност.

Поставянето на най-често срещаните формули ще помогне на учениците да се ориентират по различни начини за изчисляване на площта на трапеца и по-добра подготовка за тестове и тестове по тази тема.