Регресионно уравнение Уравнение с множествена регресия
По време на обучението си студентите често се сблъскват с различни уравнения. Една от тях - регресионното уравнение - се разглежда в тази статия. Този тип уравнение се използва специално за описание на характеристиките на връзката между математическите параметри. Този вид равенство се използва в статистиката и иконометрията.
Определение на регресия
В математиката регресията се отнася до определена стойност, която описва зависимостта на средната стойност на съвкупността от данни от стойностите на друга стойност. Регресионното уравнение показва средната стойност на друг атрибут като функция на определен атрибут. Регресионната функция има формата на просто уравнение y = x, в което y е зависимата променлива, а x е независима (знак-фактор). Всъщност регресията се изразява като y = f (x).
Какви са връзките между променливите?
Като цяло се открояват два противоположни типа взаимно свързване: корелация и регресия.
Първият се характеризира с равенство на условните променливи. В този случай не се знае надеждно коя променлива зависи от друга.
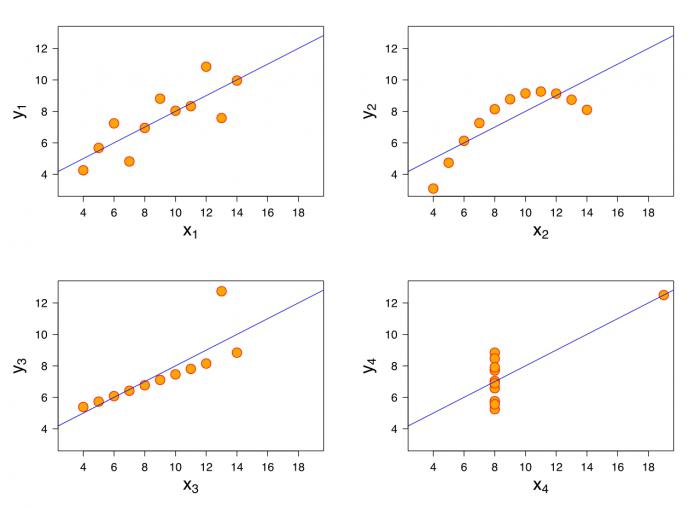
Ако не съществува равенство между променливите и в условията се казва коя променлива обяснява и която зависи, тогава можем да говорим за наличието на втори тип връзка. За да се изгради уравнение на линейна регресия, ще е необходимо да се определи какъв тип връзка се наблюдава.
Видове регресии
Към днешна дата има 7 различни типа регресия: хиперболична, линейна, множествена, нелинейна, пара, обратна, логаритмично линейна.
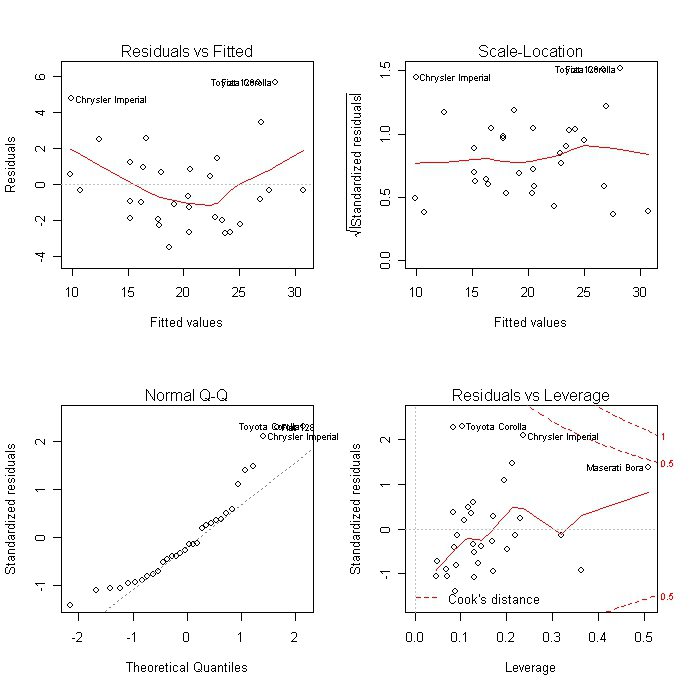
Хиперболична, линейна и логаритмична
Линейно уравнение Регресиите се използват в статистиката, за да се обяснят ясно параметрите на уравнението. Изглежда, че y = c + t * x + e. Хиперболичното уравнение има формата на редовна хипербола: y = c + t / x + E. Логаритмично линейно уравнение изразява отношение, използващо логаритмична функция: In y = In c + t * In x + In E.
Множествено и нелинейно
Два по-сложни типа регресия са множествени и нелинейни. Уравнението за множествена регресия се изразява чрез функцията y = f (x 1 , x 2 ... x c ) + E. В тази ситуация y е зависимата променлива, а x е обяснителната променлива. Променливата Е е стохастична, тя включва влиянието на други фактори в уравнението. Уравнението на нелинейната регресия е малко противоречиво. От една страна, по отношение на взетите под внимание показатели, тя не е линейна, а от друга страна, в ролята на оценка на показателите, тя е линейна.
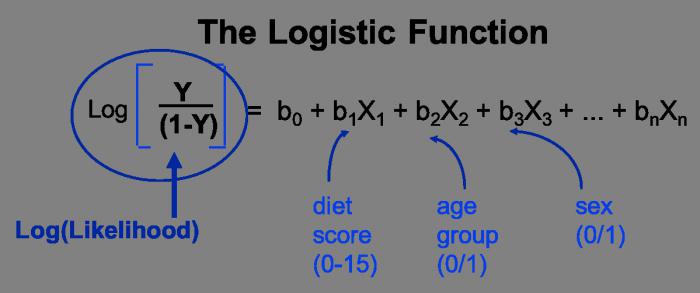
Обратни и сдвоени типове регресии
Обратното е вид функция, която трябва да се преобразува в линейна форма. В най-традиционните приложни програми, тя има формата на функция y = 1 / s + t * x + E. Уравнението на двойката регресия показва връзката между данните като функция на y = f (x) + E. Точно както в други уравнения, y зависи от x, а E е стохастичен параметър.
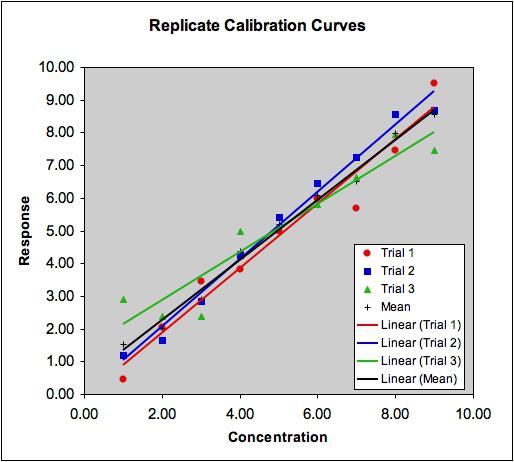
Концепцията за корелация
Това е показател, който показва наличието на връзка между две явления или процеси. Силата на връзката се изразява като коефициент на корелация. Стойността му варира в интервала [-1; +1]. Отрицателният индикатор показва наличието на обратна връзка, положителната показва пряка. Ако коефициентът приеме стойност 0, тогава няма връзка. Колкото по-близо е стойността до 1, толкова по-силна е връзката между параметрите, колкото по-близо до 0, толкова по-слаба.
методи
Корелационните параметрични методи могат да оценят близостта на връзката. Те се използват въз основа на оценката на разпределението за изследване на параметрите, които се подчиняват на закона за нормално разпределение.
Параметрите на уравнението за линейна регресия са необходими за идентифициране на вида на зависимостта, функцията на регресионното уравнение и оценката на индикаторите на избраната формула за взаимовръзка. Полето на корелация се използва като метод за идентификация на комуникацията. За да направите това, всички съществуващи данни трябва да бъдат показани графично. В правоъгълна двуизмерна координатна система е необходимо да се прилагат всички известни данни. Това представлява поле на корелация. Стойността на описващия фактор е маркирана по оста на абсцисата, а стойностите на зависимия фактор са маркирани по ордината. Ако има функционална връзка между параметрите, те са подредени във формата на линия.
Ако коефициентът на корелация на тези данни е по-малък от 30%, може да се говори за почти пълна липса на комуникация. Ако е между 30% и 70%, това показва наличието на връзки със средна плътност. 100% индикатор - доказателство за функционална комуникация.
Уравнението на нелинейната регресия, както и линейното, трябва да бъдат допълнени с индекс на корелация (R).
Корелация на множествена регресия
Коефициентът на определяне е показател за квадрата на множествената корелация. Той говори за близостта на връзката на представения набор от показатели с изследваната черта. Той може да говори и за естеството на влиянието на параметрите върху резултата. Уравнението за множествена регресия се изчислява с помощта на този индикатор.
За да се изчисли индексът на множествена корелация, е необходимо да се изчисли нейният индекс.
Метод с най-малки квадрати
Този метод е метод за оценка на регресионните фактори. Същността му се състои в минимизиране на сумата от отклонения в квадрата, получена поради зависимостта на фактора от функцията.
Уравнението по двойка линейна регресия може да бъде оценено с помощта на този метод. Този тип уравнения се използват в случаите на откриване между индикаторите на двойка линейни отношения.
Параметри на уравненията
Всеки параметър на функцията за линейна регресия има специфично значение. Уравнението на двойната линейна регресия съдържа два параметъра: s и m. Параметърът t показва средната промяна в крайния индикатор на функцията y, подлежаща на намаление (увеличаване) на променливата х с една конвенционална единица. Ако променливата x е нула, функцията е равна на параметъра c. Ако променливата x не е нула, тогава фактор c не носи икономически смисъл. Единственото влияние върху функцията има знак пред фактора c. Ако има минус, тогава можем да кажем за бавната промяна в резултата в сравнение с фактора. Ако има плюс, то това показва ускорена промяна в резултата.
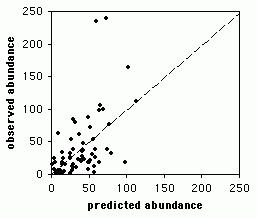
Всеки параметър, който променя стойността на регресионното уравнение, може да се изрази чрез уравнението. Например, факторът c има вида c = y - mx.
Групирани данни
Съществуват такива условия на проблема, при който цялата информация е групирана на базата на х, но в същото време за дадена група се посочват съответните средни стойности на зависимия индикатор. В този случай средните стойности описват как се променя индексът, в зависимост от x. По този начин групираната информация помага да се намери уравнение на регресия. Той се използва като анализ на връзката. Този метод обаче има своите недостатъци. За съжаление средните показатели често са обект на външни колебания. Тези трептения не са отражение на модела на връзката, те само маскират неговия “шум”. Средните стойности показват, че моделите на връзката са много по-лоши от уравнението на линейната регресия. Въпреки това, те могат да бъдат използвани като база за намиране на уравнението. Умножавайки силата на една популация със съответната средна стойност, можете да получите количеството y в групата. След това трябва да подредите всички получени суми и да намерите крайния индикатор за. Малко по-трудно да се правят изчисления със сумата на xy. В този случай, ако интервалите са малки, можете условно да вземете индикатора x за всички единици (в рамките на групата) същия. Необходимо е да се умножи със сумата y, за да се намери сумата на продуктите x по y. Освен това, всички количества се добавят заедно и се получава общото количество xy.
Уравнение за регресия с множество двойки: оценка на важността на комуникацията
Както вече бе обсъдено, множествената регресия има функция на формата y = f (x 1 , x 2 , ..., x m ) + E. Най-често подобно уравнение се използва за решаване на проблема с търсенето и предлагането на даден продукт, дохода от лихви по обратно изкупените акции, проучване на причините и вида на функцията на производствените разходи. Той също така се използва активно в голямо разнообразие от макроикономически изследвания и изчисления, но на микроикономическо ниво такова уравнение се използва малко по-малко.
Основната задача на множествената регресия е да се изгради модел на данни, съдържащ огромен количество информация за да се определи допълнително въздействието на всеки от факторите поотделно и в общата им съвкупност по отношение на индикатора, който ще се моделира, и неговите коефициенти. Регресионното уравнение може да приеме голямо разнообразие от стойности. В същото време за оценяване на взаимното свързване обикновено се използват два вида функции: линейни и нелинейни.
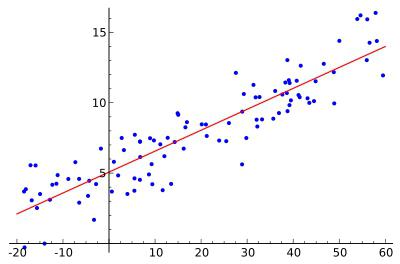
Линейната функция е представена под формата на такава взаимовръзка: y = a 0 + a 1 x 1 + a 2 x 2 , + ... + a m x m . В същото време, a2, a m , се считат за “чисти” регресионни коефициенти. Те са необходими за характеризиране на средната промяна в параметъра y с промяна (намаление или увеличаване) във всеки съответстващ параметър x с една единица, при условие на стабилна стойност на други показатели.
Нелинейните уравнения, например, имат формата на силова функция y = ax 1 b1 x 2 b2 ... x m bm . В този случай се извикват индикаторите b 1 , b 2 ..... b m коефициенти на еластичност те показват как резултатът се променя (с колко%) с увеличение (намаление) на съответния показател х с 1% и със стабилен показател за останалите фактори.
Какви фактори трябва да се вземат предвид при изграждането на множествена регресия
За правилно конструиране на множествена регресия е необходимо да се установи кои фактори трябва да се обърнат специално внимание.
Необходимо е да има известно разбиране за естеството на връзката между икономическите фактори и моделираното. Факторите, които трябва да бъдат включени, трябва да отговарят на следните критерии:
- Трябва да подлежи на количествено определяне. За да се използва фактор, който описва качеството на обекта, във всеки случай, той трябва да получи количествена форма.
- Не трябва да има взаимовръзка между факторите или функционални взаимоотношения. Такива действия най-често водят до необратими последствия - системата от обикновени уравнения става безусловна и това води до ненадеждност и неяснота на оценките.
- При наличието на огромен корелационен индикатор не може да се определи изолираното влияние на факторите върху крайния резултат от индикатора, следователно коефициентите се интерпретират.
Методи на строителство
Има огромен брой методи и методи, които обясняват как да се изберат фактори за уравнение. Въпреки това, всички тези методи се основават на избора на коефициенти, използвайки индекса на корелация. Сред тях са:
- Методът на елиминиране.
- Метод на включване.
- Поетапно регресионен анализ.
Първият метод включва премахване на всички коефициенти от кумулативния набор. Вторият метод включва въвеждането на много допълнителни фактори. А третата е елиминирането на факторите, които преди са били използвани за уравнението. Всеки един от тези методи има право да съществува. Те имат своите плюсове и минуси, но те могат да решат въпроса за премахването на ненужните показатели по свой начин. По правило резултатите, получени от всеки отделен метод, са доста близки.
Методи за мултивариантен анализ
Такива методи за определяне на факторите се основават на разглеждане на отделни комбинации от взаимосвързани характеристики. Те включват дискриминантния анализ, разпознаването на лицата, начина, по който основните компоненти и клъстерния анализ. Освен това има също така факторен анализ въпреки това се появи поради развитието на компонентния метод. Всички те се използват при определени обстоятелства при определени условия и фактори.