Моделиране - какво е това? Метод на симулация. Математическо и компютърно моделиране

За да разберем същността на математическото моделиране, вземете под внимание основните дефиниции, особености на процеса.

Същност на термина

Моделирането е процес на създаване и прилагане на модел. Счита се за всеки абстрактен или материален обект, заместващ в процеса на изучаване реалния обект на моделиране. Важното е запазването на свойствата, необходими за пълния анализ на субекта.

Компютърната симулация е версия на познанието, базирана на математически модел. Тя предполага система от неравенства, уравнения и логически изрази, които напълно отразяват всички характеристики на дадено явление или обект.

Математическото моделиране включва специфични изчисления, използване на компютърни технологии. За да се обясни процеса, са необходими допълнителни изследвания. Компютърното моделиране успешно се справя с тази задача.

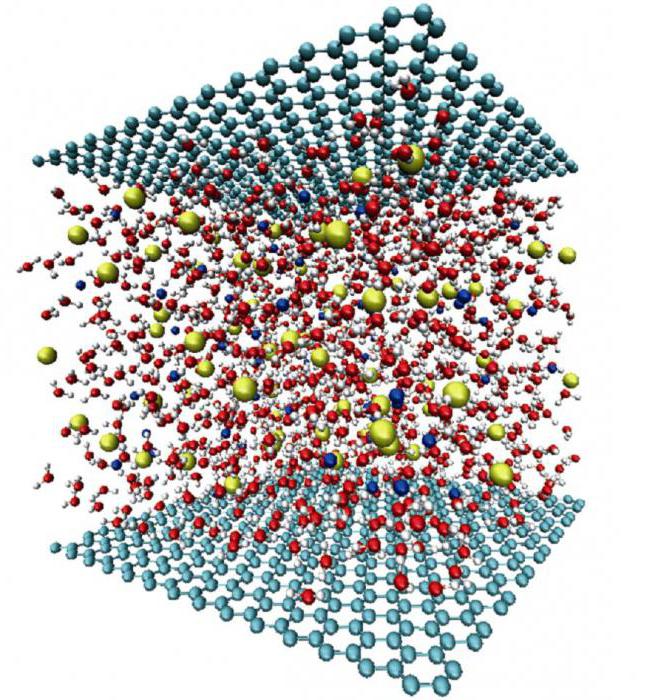
Специфика на компютърната симулация

Този метод за изучаване на сложни системи се счита за ефективен и ефикасен. По-удобно и по-лесно е да се анализират компютърни модели, тъй като могат да се извършват различни изчислителни действия. Това е особено вярно в случаите, когато поради физически или материални причини реалните експерименти не позволяват да се постигне желания резултат. Последователността на тези модели дава възможност да се определят основните фактори, които определят параметрите на изследваното оригинално.

Подобно приложение на математическото моделиране позволява да се идентифицира поведението на обект в различни условия, да се разкрие влиянието на различни фактори върху неговото поведение.

Основи на компютърната симулация

Каква е основата за такова моделиране? Какво е изследване, базирано на ИКТ? Първо, всяка компютърна симулация се основава на определени принципи:

• математическо моделиране за описване на процеса, който се изучава;
• прилагане на иновативни математически модели за подробно разглеждане на изследваните процеси.

Разнообразие от моделиране

В момента съществуват различни методи за математическо моделиране: имитационно и аналитично.

Аналитичната версия е свързана с изучаването на абстрактни модели на реален обект под формата на диференциални, алгебрични уравнения, които осигуряват извършването на ясна компютърна технология, която може да даде точно решение.

Симулацията включва изучаване на математически модел под формата на специфичен алгоритъм, който възпроизвежда функционирането на анализираната система чрез последователно изпълнение на система от прости изчисления и операции.

Характеристики на изграждането на компютърен модел

Нека разгледаме по-подробно как става това моделиране. Какви са етапите на компютърните изследвания? Първо, процесът се основава на отклонението от ясен обект или явление, което се анализира.

Такова моделиране се състои от два основни етапа: създаване на качествен и количествен модел. Компютърното изследване се състои в провеждане на система от изчислителни действия на персонален компютър с цел анализиране, систематизиране, сравняване на резултатите от изследването с действителното поведение на анализирания обект. Ако е необходимо, допълнително усъвършенстване на модела.

Етапи на моделиране

Как е симулацията? Какви са етапите на компютърните изследвания? Така че, изберете следния алгоритъм на действия, свързани с изграждането на компютърен модел:

Етап 1 Определяне на целите и задачите на работата, идентифициране на обекта на моделиране. Целта е да се съберат данни, да се постави въпрос, да се определят целите и формите на изследването, да се опишат получените резултати.

Етап 2 Анализ и изследване на системата. Извършва се описание на обекта, създаване на информационен модел, избор на софтуер и хардуер, се подбират примери за математическо моделиране.

Етап 3 Преход към математически модел, изработване на метода на проектиране, избор на алгоритъм на действие.

4 етап. Избор на език за програмиране или средство за моделиране, обсъждане на възможности за анализ, записване на алгоритъм в специфичен език за програмиране.

Етап 5 Той се състои в провеждане на комплекс от изчислителни експерименти, изчисления на грешки и обработка на получените резултати. Ако е необходимо, на този етап, коригирането на симулацията.

6 етап. Тълкуване на резултатите.

Как се анализира симулацията? Какво е изследователски софтуер? На първо място, това предполага използването на текстови, графични редактори, електронни таблици, математически пакети, които ви позволяват да получите максималния резултат от изследването.

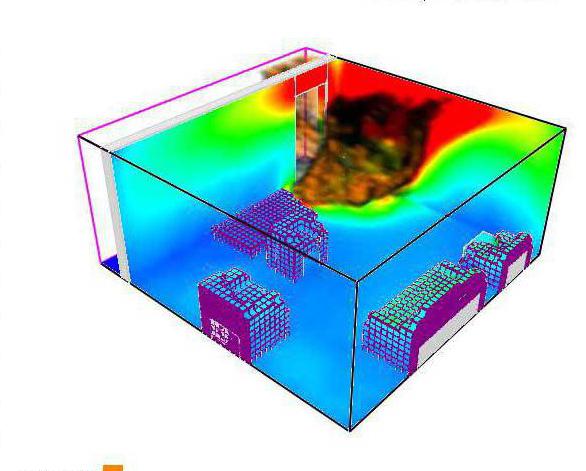
Провеждане на изчислителен експеримент

Всички методи на математическо моделиране са базирани на експерименти. Под тях обикновено се разбират експерименти с модел или обект. Те се състоят в изпълнението на определени действия, позволяващи да се определи поведението на експерименталната проба в отговор на предложените действия.

Невъзможно е да си представим изчислителен експеримент, без да се правят изчисления, свързани с използването на формализиран модел.

Основите на математическото моделиране включват изследване с реален обект, но изчислителните операции се извършват с неговото точно копие (модел). При избора на определен набор от първоначални показатели на модела, след завършване на изчислителните действия, е възможно да се получат оптимални условия за пълно функциониране на реален обект.

Например, имайки математическо уравнение, което описва потока на анализирания процес, когато се променят коефициентите, началните и междинните условия, можем да приемем поведението на обекта. В допълнение, можете да създадете надеждна прогноза за поведението на този обект или природен феномен при определени условия. В случай на нов набор от изходни данни е важно да се проведат нови изчислителни експерименти.

Сравнение на данните

За да се извърши адекватна проверка на реален обект или създаден математически модел, както и да се оценят резултатите от изследванията на компютърните технологии с резултатите от експеримент, проведен на пълна експериментална извадка, се прави сравнение на резултатите от изследванията.

От какво несъответствие между информацията, получена в хода на изследването, зависи от решението да се изгради завършен образец или да се коригира математическият модел.

Такъв експеримент дава възможност да се заменят естествените скъпи изследвания с изчисления върху компютърните технологии, за възможно най-кратък срок, за да се анализират възможностите за използване на обекта, да се идентифицират условията за неговото действително функциониране.

Моделиране в среда

Например, програмата за програмиране използва три етапа на математическото моделиране. На етапа на създаване на алгоритъма и информационния модел те определят стойностите, които ще бъдат входните параметри, резултатите от изследването и техния тип.

Ако е необходимо, направете специални математически алгоритми под формата на блок-схеми, написани на специфичен език за програмиране.

След това се извършва самият изчислителен експеримент, за който програмата се зарежда в оперативната памет на изчислителното устройство, след което се започва процесът на изчисление.

Компютърният експеримент включва анализ на резултатите, получени при изчисленията, тяхната корекция. Сред важните етапи на такова проучване, ние отбелязваме тестването на алгоритъма, анализа на работоспособността на програмата.

Отстраняването на грешки включва откриване и отстраняване на грешки, които водят до нежелан резултат, поява на грешки в изчисленията.

Тестването включва проверка на правилното функциониране на програмата, както и оценка на надеждността на отделните му компоненти. Процесът се състои в проверка на работата на програмата, нейната пригодност за изучаване на определено явление или обект.

електронни таблици

Моделирането с помощта на електронни таблици ви позволява да покриете голям брой задачи в различни тематични области. Те се считат за универсален инструмент, който ви позволява да решите отнемащата време задача за изчисляване на количествените параметри на обекта.

В случая на тази версия на симулацията, има някаква трансформация на алгоритъма за решаване на проблема, няма нужда да се разработва изчислителен интерфейс. В този случай има етап на отстраняване на грешки, който включва премахване на грешки в данните, търсене на връзки между клетките, идентификация на изчислителни формули.

С напредването на работата се появяват допълнителни задачи, например извеждане на резултати на хартиени носители, рационално представяне на информация на компютърен монитор.

Последователност от действия

Моделирането се извършва в електронна таблица за конкретен алгоритъм. Първо се определят изследователските цели, идентифицират се основните параметри и взаимовръзки, а въз основа на получената информация се съставя конкретен математически модел.

За качествено разглеждане на модела се използват първоначалните, междинните и крайните характеристики, които ги допълват с чертежи, диаграми. С помощта на графики и диаграми се получава визуално представяне на резултатите от работата.

Моделиране в среда на СУБД

Тя позволява да се решат следните задачи:

• съхранява информация, провежда своевременно редактиране;
• организира наличните данни на конкретни основания;
• създаване на различни критерии за избор на данни;
• представете наличната информация по удобен начин.

Тъй като моделът е разработен на базата на изходни данни, се създават оптимални условия за описване на характеристиките на даден обект чрез специални таблици.

Същевременно се сортира информацията, търсят се и се филтрират, създават се алгоритми за извършване на изчисления. С помощта на компютърния информационен панел можете да създавате различни екранни форми, както и опции за получаване на отпечатани хартиени доклади за напредъка на експеримента.

Ако получените резултати не съвпадат с планираните варианти, те променят параметрите, провеждат допълнителни изследвания.

Прилагане на компютърен модел

Изчислителният експеримент и компютърната симулация са нови научни методи изследвания. Те ви позволяват да надстроите изчислителното устройство, използвано за изграждане на математически модел, да уточните, прецизирате, усложните експериментите.

Сред най-обещаващите за практическа употреба, пълноправен изчислителен експеримент, проектиране на реактори за мощни атомни електроцентрали. В допълнение, това включва създаването на магнитохидродинамични преобразуватели на електрическа енергия, както и балансиран дългосрочен план за страната, региона, промишлеността.

С помощта на компютърно и математическо моделиране можем да проектираме устройствата, необходими за изучаване на термоядрените реакции и химичните процеси.

Компютърната симулация и изчислителните експерименти дават възможност да се намалят далеч "не-математическите" обекти за компилирането и решаването на математически проблем.

Това създава големи възможности за прилагане на математическия апарат в система с модерна компютърна технология за решаване на проблеми, свързани с овладяването на космическото пространство, „завладяването” на атомните процеси.

Именно моделирането се превърна в един от най-важните варианти на познаване на различни околни процеси и природни феномени. Това знание е сложен и отнемащ много време процес, включващ използването на система от различни типове моделиране, като се започне с разработването на редуцирани модели на реални обекти, завършвайки подбора на специални алгоритми за сложни математически изчисления.

В зависимост от това какви процеси или явления ще бъдат анализирани, се избират определени алгоритми на действия, математически формули за изчисления. Компютърната симулация позволява получаване на желания резултат, важна информация за свойствата и параметрите на обект или явление с минимални разходи.