Как да намерим корен квадратен? Свойства, примери за извличане на корена
Математиката възниква, когато човек осъзнава себе си и започва да се позиционира като автономна единица на света. Желанието да измерите, сравните, изчислите онова, което ви заобикаля - това е в основата на една от фундаменталните науки на нашето време. Първоначално това бяха части от елементарна математика, което ни позволи да свържем числата с техните физически изрази, по-късни заключения бяха представени само теоретично (по силата на тяхната абстрактност), а след известно време, както казва един учен, "математиката достигна тавана на сложност, когато изчезна всички числа. " Понятието "квадратен корен" се появява в момент, когато може лесно да бъде подкрепен от емпирични данни, надхвърлящи равнината на изчисление.
Как започна всичко
Първото споменаване на корена, което в момента се обозначава като √, е записано в писанията на вавилонските математици, които инициирали съвременната аритметика. Разбира се, те изглеждаха малко като сегашната форма - учени от тези години първо използваха обемисти таблетки. Но през второто хилядолетие пр. Хр. д. те извличат приблизителна формула за изчисление, която показва как да се извлече квадратният корен. На снимката по-долу е показан камък, върху който вавилонските учени са изрязали процеса на ,2, и се оказа толкова вярно, че несъответствието в отговора е намерено само в десетия знак след десетичната запетая. 
В допълнение, коренът е бил използван, ако е необходимо да се намери страната на триъгълника, при условие, че другите две са известни. Е, когато решаваш квадратни уравнения От извличането на корена не може да отиде никъде.
Заедно с вавилонските произведения, предметът на статията е изследван и в китайската работа "Математика в девет книги", а древните гърци стигат до заключението, че всеки брой, от който не се извлича корен без остатък, дава ирационален резултат.
Произходът на този термин е свързан с арабското представяне на числото: древните учени вярвали, че квадратът на произволен брой расте от корена, подобно на растение. На латиница, тази дума звучи като радикал (можете да проследите модела - всичко, което има корен, което означава, че товарът е съгласен, било то ряпа или радикулит).
Учените от следващо поколение взеха тази идея, определяйки я като Rx. Например, през XV век, за да покаже, че квадратен корен е извлечен от произволно число а, те пишат R 2 a. Познатото „кърлежи“ се появява едва през 17 век благодарение на Рене Декарт.
Нашите дни
От гледна точка на математиката, квадратният корен на y е такъв брой z, чийто квадрат е равен на y. С други думи, z 2 = y е еквивалентно на =y = z. Тази дефиниция обаче е релевантна само за аритметичния корен, тъй като предполага не-отрицателна стойност на израза. С други думи, =y = z, където z е по-голямо или равно на 0. 
Като цяло, това, което работи за дефиниране на алгебричен корен, стойността на израз може да бъде и положителна, и отрицателна. Така, поради факта, че z 2 = y и (-z) 2 = y, имаме: =y = ± z или =y = | z |.
Поради факта, че любовта към математиката с развитието на науката се е повишила, има различни прояви на привързаност към нея, които не се изразяват в сухи изчисления. Например, в еднаква степен с такива забавни явления като деня на Пи, празнуваме и коренните корени. Те се маркират девет пъти за сто години и се определят по следния принцип: числата, които означават ден и месец по ред, трябва да са квадратният корен от годината. Така че следващия път трябва да празнуваме този празник на 4 април 2016 г.
Свойства на квадратния корен в полето R
- Квадратният корен на продукта е равен на произведението на квадратни корени, при условие че радикалните изрази са по-големи или равни на 0.
- При издигането на квадратен корен е достатъчно да се издигне до тази сила радикален израз, при условие че той е по-голям от нула.
- Квадратният корен на една дроб е равен на корена на числителя, разделен на корена на знаменателя, при условие че квадратният корен на числителя е по-голям или равен на 0, а квадратният корен на знаменателя е строго по-голям от 0.
- Радикалният израз, ако е по-голям от нула, може да бъде разделен на няколко части, от които на свой ред е разрешено да се извлече коренът. Например: =75 = *25 * 3 = 5√3.
- Под знака на корена можете да въведете произволен брой, като го вдигнете в квадрат. Например: 5√8 = *25 * =8 = .200.
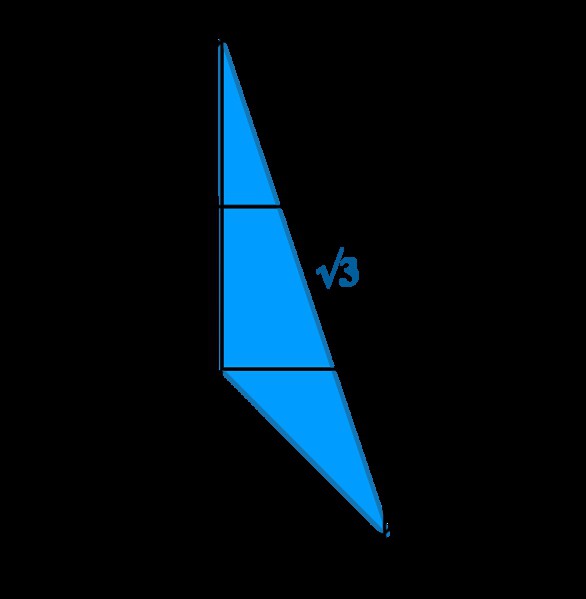
Практически всички математически изрази имат геометрична основа под тях, тази съдба и ,y, която се дефинира като страна на квадрат с площ от y, не избяга.
Как да намерим корена на числото?
Има няколко алгоритма за изчисления. Най-простото, но доста тромаво е обичайното аритметично изчисление, което се състои от следното:
1) от номера, чийто корен ни е необходим, се изважда на свой ред нечетни числа - докато изходният баланс е по-малък от приспадащия, или дори нулев. Броят на ходовете и в крайна сметка ще бъде желания номер. Например, изчисляване на квадратен корен от 25:
25-1 = 24
24-3 = 21
21-5 = 17
17-7 = 10
10-9 = 1
Следващото нечетно число е 11, а останалото е следното: 1 <11. Броят на ходовете е 5, така че коренът на 25 е 5. Всичко изглежда лесно и просто, но представете си какво трябва да изчислите от 18769?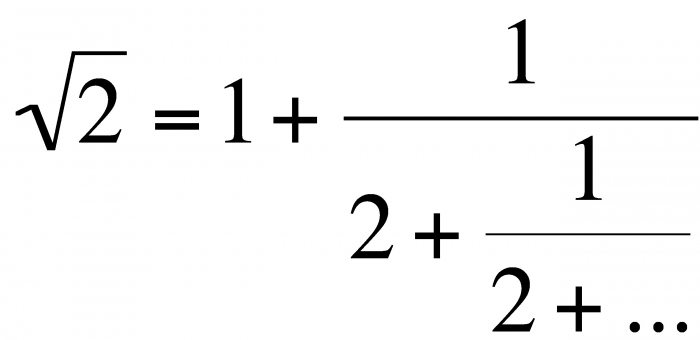 
За такива случаи в серията Тейлър има декомпозиция:
√ (1 + y) = ∑ ((- 1) n (2n)! / (1-2n) (n!) 2 (4 n )) y n , където n приема стойности от 0 до
+ ∞, и | y | ≤1.
Графично представяне на функцията z = √y
Разгледайте елементарна функция z = ony в полето на реалните числа R, където y е по-голямо или равно на нула. Нейният график е както следва: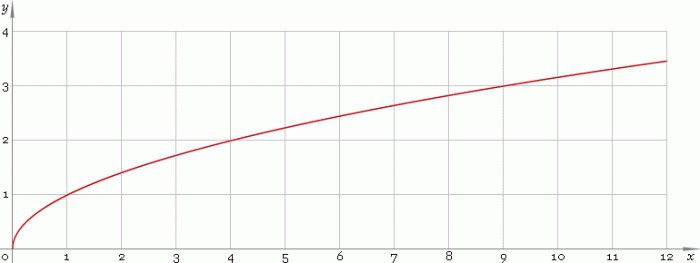 
Кривата расте от произхода и непременно пресича точката (1; 1).
Свойства на функцията z = √y върху полето на реалните числа R
1. Областта на разглежданата функция е интервалът от нула до плюс безкрайност (нула е включена).
2. Обхватът на стойностите на въпросната функция е интервалът от нула до плюс безкрайност (нула е включена отново).
3. Минималната стойност на (0) функцията заема само в точката (0; 0). Липсва максималната стойност.
4. Функцията z = √y не е нито четна, нито нечетна.
5. Функцията z = √y не е периодична.
6. Точката на пресичане на графиката на функцията z = √y с осите на координатите е само една: (0; 0).
7. Точката на пресичане на графиката на функцията z = √y също е нула на тази функция.
8. Функцията z = continuouslyy непрекъснато расте.
9. Функцията z = √y заема само положителни стойности, следователно графът й заема първия координатен ъгъл.
Варианти на функцията на изображението z = .y
В математиката, за да се улесни изчисляването на сложни изрази, понякога се използва форма на власт, за да се напише квадратният корен: =y = y 1/2 . Такава опция е удобна, например, при издигане на функция към силата: ()y) 4 = (y 1/2 ) 4 = y 2 . Този метод също е добра идея за диференциране с интеграция, тъй като поради него квадратният корен е представен от обикновена силова функция.
А при програмирането, заместването на is символа е комбинацията от букви sqrt. 
Трябва да се отбележи, че в тази област квадратен корен е много в търсенето, тъй като е част от повечето от геометричните формули, необходими за изчисленията. Самият алгоритъм за броене е доста сложен и е изграден на базата на рекурсия (функция, която се нарича сама).
Квадратен корен в комплексно поле C
Като цяло, това е предмет на тази статия, която стимулира отварянето на полето. сложни числа В, тъй като математиците не са били спокойни с въпроса за получаване на корен от равномерна степен от отрицателно число. Така се появява въображаемата единица, която се характеризира с много интересно свойство: неговият квадрат е -1. Благодарение на това се получават квадратични уравнения и с отрицателен дискриминант. В C, за квадратен корен, същите свойства като в R са релевантни, единственото нещо е, че ограниченията върху радикана са премахнати.