Как да се изгради графика на линейна функция. примери
За да се разбере как да се начертае линейна функция, е важно да се разбере самата същност на функцията. Функцията е модел на зависимостта на промените на един параметър от друг.
Темата за функционалните зависимости традиционно се отваря с линейна функционална зависимост. Линейното е най-простата зависимост. Графиката на линейната функция е права.
Живот и функция
В живота, линейните зависимости обикновено се намират в идеални изкуствени процеси, като промените в които се приемат за постоянни. Например, когато човек отива някъде с постоянна скорост.
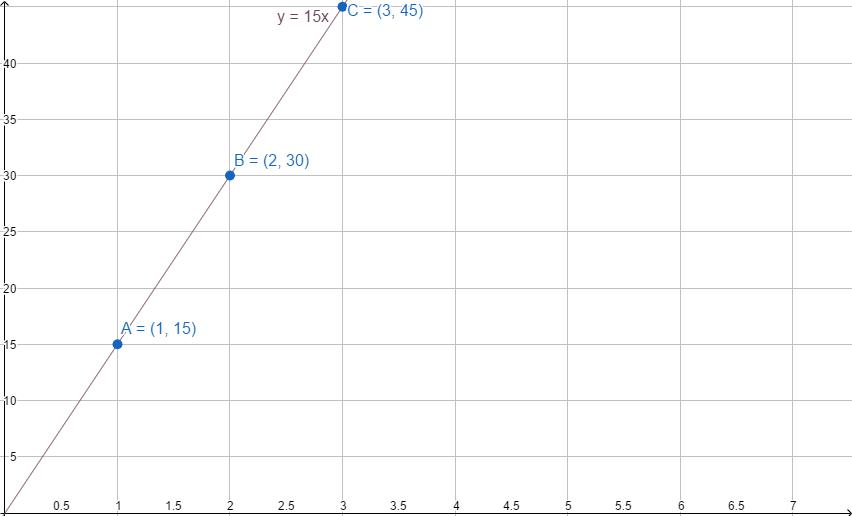
Разстоянието, което човек ще пътува с велосипед, ще варира линейно в зависимост от броя на часовете, които пътува. Ако премине 15 километра за час (точка А), то след два часа ще измине 30 километра (точка Б), след три часа - 45 (точка В).
Зависимостта е описана с уравнението y = 15x. Как да начертаем линейна функция в този случай?
- намери координатите на точките, които са решението на уравнението;
- да ги изгради на координатна равнина;
- свържете тези точки към линия.
Описание на алгоритъма
Търсенето на координатите на точките, които са решения на уравнението, намалява до намирането на две точки, които еднозначно дефинират линия. Въпреки че е достатъчно да се изберат две различни стойности на x и да се намерят съответните стойности на y, могат да бъдат намерени три двойки стойности за самоконтрол. Това ще ви позволи бързо да идентифицирате възможна грешка в изчисленията. Често първата стойност на x е избрана да бъде нула.
| y = 15x | (0, 0) | (1, 15) |
| x = 0 | x = 1 | |
| y = 15 × 0 | y = 15 × 1 | |
| у = 0 | y = 15 |
Втората стойност на x за големи k е по-добре да се избере до първата. В противен случай ще има силно разсейване на стойностите на y и x, например при x = 4 в разглежданото уравнение, y = 60. Във всеки случай, преди да се начертае линейна функция върху намерените точки, се избира скала.
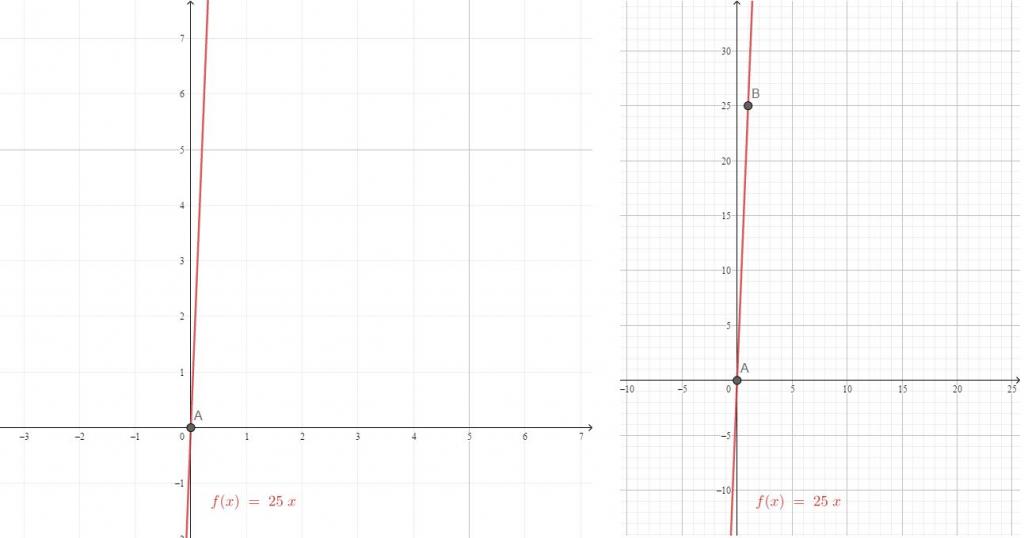
| у = 25 х | (0, 0) | (1, 25) |
| x = 0 | x = 1 | |
| y = 25 × 0 | y = 25 × 1 | |
| у = 0 | y = 25 |
Коефициент за x
Уравнението на линейната функция е от вида y = kx + b. В зависимост от промяната на коефициента за неизвестното, естеството на графиката на линейната функция y = kx също се променя.
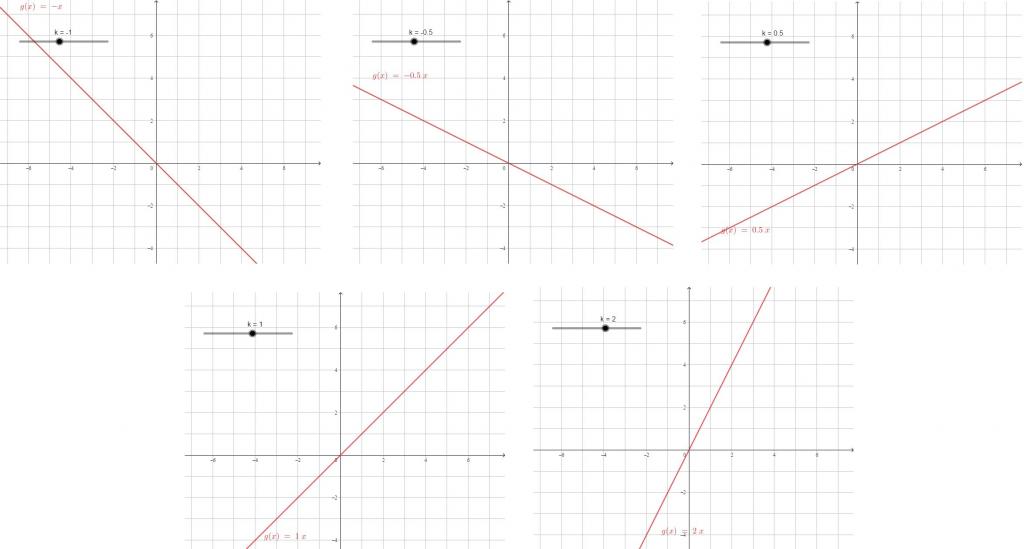
Колкото по-голям е коефициентът на модул, толкова по-голяма е стръмността на линията, толкова по-силна за същата промяна в х стойностите на y се променят. Коефициентът на х е коефициентът на пропорционалност.
Безплатно съотношение
Свободният коефициент е константа, която не зависи от промените в стойността на x. Той показва къде линията пресича OY.
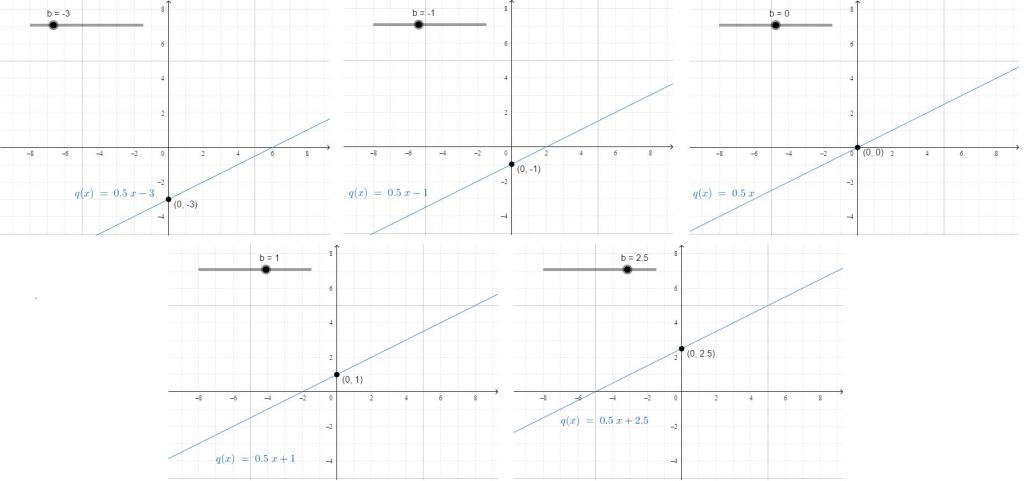
Например, един човек е ходил 10 километра от сутринта до 12 часа следобед и след това е карал велосипед за три часа. Тогава разстоянието, което е покрило за деня: y = 15 × 3 + 10. Ако искате да извлечете формула за изчисляване на разстоянието в края на всеки час от трите, които е яздил на велосипед, можете да използвате: y = 15x + 10. В един час ден той караше 15 × 1 и още 10 минаха, в два часа той караше 15 × 2, но минаваше все пак 10.
Графиката на линейната функция y = kx + b описва линия, която има наклон k и пресича OY в точката с координати (0, b). Анализът на уравнението често ви позволява да решавате проблеми, без да изграждате графика. Но за да работим в ума, действията трябва да бъдат добре прикрепени към визуалния материал.
Например, задачата е да се намерят точките на пресичане y = - x 2 и y = 0.5x + 5. Първата функция намалява, втората се увеличава, първата е под втората, защото клоновете на параболата са надолу, а нейният връх е в началото. Линейната функция би трябвало да има много по-голям ъгъл на наклон, за да бъде по-стръмна и да пресича един от клоните на параболата. Следователно е възможно да се определи недвусмислено, че няма пресечни точки без изграждане на графика и без да се правят замествания.
Специални случаи
- Когато няма свободен коефициент, той е (всъщност) равен на нула, което означава, че правата линия пресича OY при нула.
- Когато няма неизвестни x или y, y и x са независими един от друг. Например y = 5. Без значение каква стойност x е, y винаги ще бъде 5. Графично това може да бъде представено като права линия, успоредна на OX.
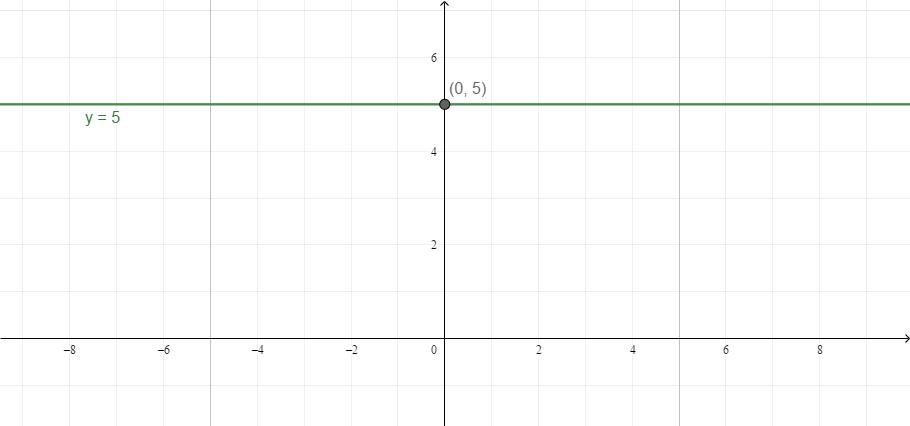
- Същото важи и за случая, когато променливата x е равна на числото: променливата x има постоянна стойност.
Чрез анализиране на уравнението преди начертаването на линейна функция, можете да откриете приблизителното му местоположение на OY и ъгъла на наклона, а оттам и наклона. Това помага не само да се намери правилната скала и да се изгради графика, но и да се решат някои проблеми в ума.