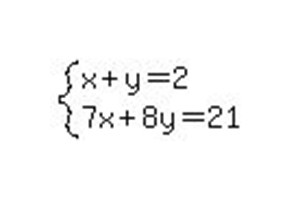Гаусов метод за решаване на матрици. Решение на система от линейни уравнения по метода на Гаус

От началото на XVI-XVIII век, математиците започнали да изучават интензивно функциите, поради които толкова много се е променило в живота ни. Компютърните технологии без това знание просто нямаше да съществуват. За решаването на сложни задачи, линейни уравнения и функции са създадени различни концепции, теореми и методи за решение. Един от тези универсални и рационални методи и методи за решаване на линейни уравнения и техните системи е методът на Гаус. Матриците, техният ранг, определящ фактор - всичко може да се изчисли, без да се използват сложни операции.

Какво е slau

В математиката съществува концепцията за SLAE - система от линейни алгебрични уравнения. Каква е тя? Това е набор от m уравнения с неизвестни променливи n неизвестни, обикновено означени като x, y, z или x ₁ , x ₂ ... x _n или други символи. За да се реши тази система, използвайки метода на Гаус, трябва да се намерят всички неизвестни неизвестни. Ако системата има същия брой неизвестни и уравнения, тя се нарича система от n-ти ред.

Най-популярните методи за решаване на slf

В образователните институции на средното образование те изучават различни методи за решаване на такива системи. Най-често това са прости уравнения, състоящи се от две неизвестни, така че всеки съществуващ метод за намиране на отговор на тях няма да отнеме много време. Това може да бъде метод на заместване, когато друг се извлича от едно уравнение и се замества с първоначалното. Или методът на термина чрез изваждане и добавяне. Но методът на Гаус се счита за най-лесен и универсален. Това позволява да се решават уравнения с произволен брой неизвестни. Защо тази техника се счита за рационална? Това е просто. Методът на матрицата е добър, защото няма нужда да се презаписват ненужни символи няколко пъти като неизвестни, достатъчно е да се правят аритметични операции върху коефициентите - и получавате надежден резултат.

Къде се използват SLAE на практика

Решението на SLAE е пресечните точки на линиите на графиките на функциите. В нашата високотехнологична компютърна възраст хората, които са тясно свързани с развитието на игри и други програми, трябва да знаят как да решават такива системи, какво представляват и как да проверяват коректността на получените резултати. Най-често програмистите разработват специални компютърни програми за линейна алгебра и това включва система от линейни уравнения. Методът на Гаус ви позволява да изчислите всички съществуващи решения. Използват се и други опростени формули и техники.

Критерий за съвместимост SLAU

Такава система може да бъде решена само ако е съвместима. За яснота ние представяме SLAE като Ax = b. Той има решение, ако rang (A) е равно на rang (A, b). В този случай (А, б) е матрица с разширен тип, която може да бъде получена от матрица А чрез пренаписване с свободни членове. Оказва се, че решават линейни уравнения Методът на Гаус е доста лесен.

Може би някаква нотация не е напълно ясна, така че трябва да погледнете всичко с пример. Да предположим, че има система: x + y = 1; 2x-3y = 6. Състои се само от две уравнения, в които 2 са неизвестни. Системата ще има решение само ако рангът на матрицата му е равен на ранга на разширената матрица. Какво е рангът? Това е броят на независимите линии на системата. В нашия случай рангът на матрицата е 2. Матрицата А ще се състои от коефициентите, разположени близо до неизвестните, а коефициентите зад знака „=“ също се вписват в разширената матрица.

Защо SLAE може да бъде представена в матрична форма

Въз основа на критерия за съвместимост съгласно доказаната теорема на Кронекер-Капели, системата от линейни алгебрични уравнения може да бъде представена в матрична форма. Използвайки каскадния метод на Гаус, можете да решите матрицата и да получите единствения надежден отговор за цялата система. Ако рангът на обикновената матрица е равен на ранга на разширената му матрица, но е по-малък от броя на неизвестните, тогава системата има безкраен брой отговори.

Матрични трансформации

Преди да пристъпим към решаване на матрици, е необходимо да знаем какви действия могат да бъдат извършени върху техните елементи. Има няколко елементарни преобразувания:

• Чрез пренаписване на системата в матричен изглед и прилагане на нейното решение е възможно да се умножат всички елементи на един ред с един и същ коефициент.
• За да превърнете матрицата в канонична форма, можете да обменяте два паралелни реда. Каноничната форма предполага, че всички елементи на матрицата, които са разположени на главния диагонал, стават единици, а останалите - нули.
• Съответните елементи на паралелните редове на матрицата могат да се добавят един към друг.

Метод Йордан-Гаус

Същността на решаването на системи от линейни хомогенни и неоднородни уравнения с метода на Гаус е постепенното елиминиране на неизвестните. Да предположим, че имаме система от две уравнения, в които има две неизвестни. За да ги намерите, трябва да проверите системата за съвместимост. Уравнението по метода на Гаус е решено много просто. Необходимо е да се напишат коефициентите, разположени близо до всяко неизвестно в матричния изглед. За да решите системата, ще трябва да напишете разширената матрица. Ако едно от уравненията съдържа по-малък брой неизвестни, тогава е необходимо да се постави "0" на мястото на липсващия елемент. Всички известни методи за преобразуване се прилагат към матрицата: умножение, деление по номер, прибавяне на съответните елементи на редовете един към друг и други. Оказва се, че във всеки ред е необходимо да се остави една променлива със стойността "1", а останалата част да доведе до нулева форма. За по-точно разбиране е необходимо да се разгледа методът на Гаус с примери.

Един прост пример за системно решение 2x2.

Първо ще вземем проста система от алгебрични уравнения, в която ще има 2 неизвестни.

Препишете го в разширена матрица.

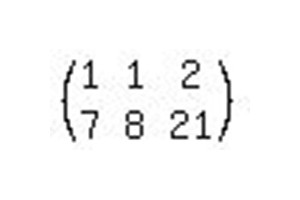
За да се реши тази система от линейни уравнения, е необходимо да се направят само две операции. Трябва да приведем матрицата в канонична форма, така че единиците да стоят по главния диагонал. Така, прехвърляйки от матричния изглед обратно към системата, получаваме уравнения: 1x + 0y = b1 и 0x + 1y = b2, където b1 и b2 са получените отговори в процеса на решение.

1. Първата стъпка при решаването на разширената матрица ще бъде: първият ред трябва да се умножи по -7 и съответните елементи да се добавят съответно към втория ред, за да се отървем от едно неизвестно във второто уравнение.
2. Тъй като решението на уравненията по метода на Гаус предполага редукция на матрицата в канонична форма, тогава е необходимо да се извършат същите операции с първото уравнение и да се премахне втората променлива. За да направим това, изваждаме втората линия от първата и получаваме необходимия отговор - решението SLAU. Или, както е показано на фигурата, втората линия се умножава по коефициента -1 и елементите на втория ред се добавят към първия ред. Това е едно и също нещо.

Както виждате, нашата система е решена чрез метода Йордан-Гаус. Презаписваме го в необходимата форма: x = -5, y = 7.

Пример за 3x3 SLAE разтвор

Да предположим, че имаме по-сложна система от линейни уравнения. Методът на Гаус позволява да се изчисли отговора дори за привидно объркващата система. Ето защо, за да се получи по-задълбочен поглед върху метода на изчисление, може да се премине към по-сложен пример с три неизвестни.

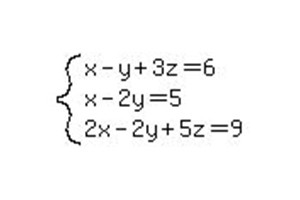
Както и в предишния пример, пренаписваме системата под формата на разширена матрица и започваме да я свеждаме до канонична форма.

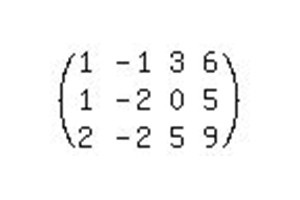
За да разрешите тази система, ще трябва да направите много повече стъпки, отколкото в предишния пример.

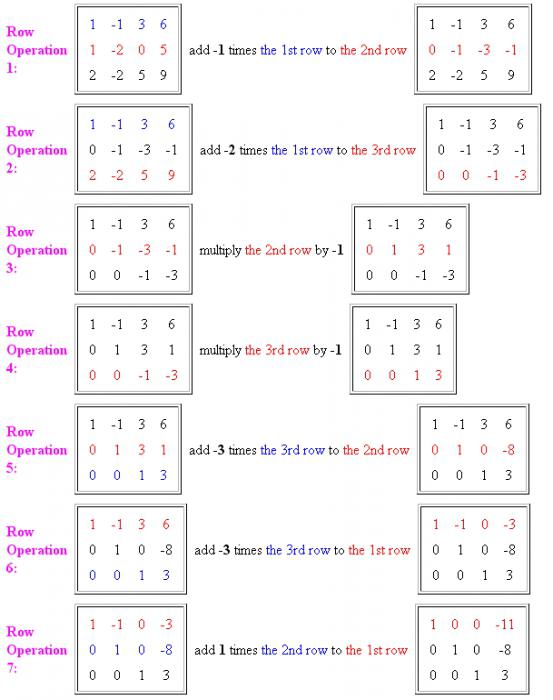
1. Първо трябва да направите в първата колона един елемент и останалите нули. За да направите това, умножете първото уравнение с -1 и добавете второто уравнение към него. Важно е да запомните, че пренаписваме първия ред в неговата оригинална форма, а втората в модифицираната.
2. След това премахнете първото неизвестно от третото уравнение. За да направите това, елементите на първия ред се умножават по -2 и се добавят към третия ред. Сега първата и втората редове се пренаписват в оригиналната форма, а третата - вече с промените. Както се вижда от резултата, получихме първата единица в началото на основния диагонал на матрицата и останалите нули. Някои повече действия и системата от уравнения, използващи метода на Гаус, ще бъдат надеждно решени.
3. Сега е необходимо да се извършват операции върху други елементи от редовете. Третото и четвъртото действие могат да бъдат обединени в едно. Необходимо е да разделим втората и третата линия с -1, за да се отървем от отрицателните единици по диагонал. Третият ред вече доведе до необходимата форма.
4. След това въвеждаме втората линия в каноничната форма. За да направите това, умножете елементите на третия ред с -3 и ги добавете към втория ред на матрицата. Резултатът показва, че втората линия също е сведена до формата, от която се нуждаем. Остава да извършите още няколко операции и да премахнете коефициентите на неизвестните от първия ред.
5. За да направите 0 от втория елемент на линията, е необходимо да умножите третия ред с -3 и да го добавите към първия ред.
6. Следващата важна стъпка ще бъде добавянето към първия ред на необходимите елементи от втория ред. Така получаваме каноничната форма на матрицата и съответно отговора.

Както виждате, решението на уравненията по метода на Гаус е доста просто.

Пример за решаване на 4х4 система от уравнения

Някои по-сложни системи от уравнения могат да бъдат решени чрез метода на Гаус чрез компютърни програми. Необходимо е да се въведат в съществуващите празни клетки коефициентите с неизвестни, а самата програма ще стъпка по стъпка изчислява необходимия резултат, описвайки подробно всяко действие.

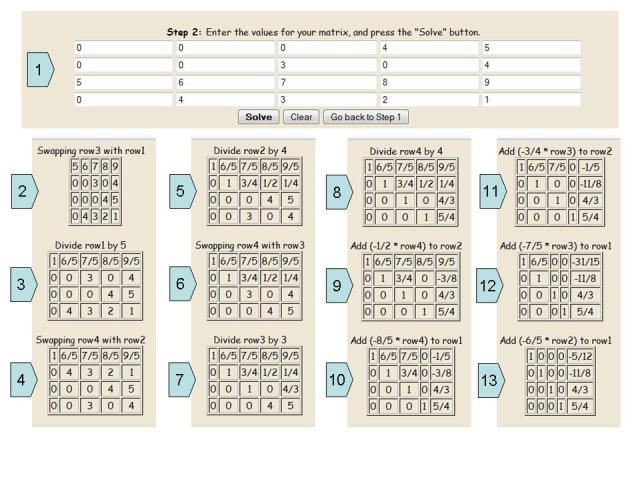
По-долу е дадено инструкции стъпка по стъпка за решаване на такъв пример.

• В първия етап свободните коефициенти и числата с неизвестни стойности се вписват в празни клетки. Така се оказва една и съща удължена матрица, която пишем на ръка.

• След това всички линии са обърнати, така че елементите на елементите да могат да бъдат изразени по главния диагонал.

• И всички необходими аритметични операции се изпълняват, за да се приведе разширената матрица в канонична форма. Трябва да се разбере, че отговорът на системата от уравнения не винаги е един и същ - те са цели числа. Понякога решението може да е от частични числа.

Решение за валидиране

Методът Йордан-Гаус осигурява проверка на коректността на резултата. За да се установи дали коефициентите са правилно изчислени, е необходимо единствено да се замени резултата в първоначалната система от уравнения. Лявата страна на уравнението трябва да съответства на дясната страна, която е зад знака за равенство. Ако отговорите не съвпадат, тогава трябва да преизчислите системата или да се опитате да приложите към нея друг метод за решаване на SLAE, който ви е известен, като заместване или термично изваждане и добавяне. В края на краищата, математиката е наука, която има огромен брой различни решения. Но не забравяйте: резултатът трябва винаги да бъде същият, без значение какъв метод да използвате.

Метод на Гаус: Най-често срещаните грешки при решаване на SLAE

При решаването на линейни системи от уравнения най-често се появяват грешки като неправилно прехвърляне на коефициенти към матричната форма. Има системи, в които някои неизвестни липсват в едно от уравненията, след което, прехвърляйки данните към разширената матрица, те могат да бъдат загубени. В резултат, при решаването на тази система, резултатът може да не съответства на реалния.

Друга от основните грешки може да бъде неправилното писане на крайния резултат. Необходимо е ясно да се разбере, че първият коефициент ще съответства на първото неизвестно от системата, второто на второто и т.н.

Методът на Гаус подробно описва решението на линейните уравнения. Благодарение на него е лесно да се извършат необходимите операции и да се намери правилния резултат. В допълнение, той е универсален инструмент за намиране на надежден отговор на уравнения от всяка сложност. Може би затова толкова често се използва при решаване на SLAE.