Десетични дроби и действия с тях. Десетично разделяне и умножение

Десетичната дроб се използва, когато трябва да извършите действия с нецели числа. Това може да изглежда ирационално. Но този вид числа значително улеснява математическите операции, които трябва да се извършват с тях. Това разбиране идва с времето, когато записът им става познат, а четенето не предизвиква трудности и се усвояват правилата на десетичните дроби. Нещо повече, всички действия повтарят вече известни, от които се научават естествени числа. Просто трябва да запомните някои функции.

Десетична дефиниция на дроби

Десетичната дроб е специално представяне на не-цяло число с знаменател, делимо на 10, и отговорът се получава като единица и, вероятно, с нули. С други думи, ако знаменателят е 10, 100, 1000 и т.н., тогава е по-удобно да се пренапише числото със запетая. Тогава цялата част ще бъде разположена преди нея, а след това и частичната част. Освен това записването на втората половина на броя ще зависи от знаменателя. Броят на цифрите, които са в дробната част, трябва да бъде равен на ранга на знаменателя.

Можете да илюстрирате горното с тези номера:

9/10 = 0.9; 178/10000 = 0,0178; 3,05; 56 003,7006.

Причини за използването на десетични дроби

Математиците взеха десетични дроби по няколко причини:

1. Опростете записа. Такава фракция е разположена по протежение на една линия, без да има тире между знаменателя и числителя, докато видимостта не страда.

2. Простота в сравнение. Достатъчно е само да съпоставите числата в еднакви позиции, докато с обикновени дроби трябва да ги донесете до общ знаменател.

3. Опростете изчисленията.

4. Калкулаторите не са предназначени за въвеждане на обикновени фракции, те използват десетичен запис за всички операции.

Как да четем такива числа?

Отговорът е прост: точно като обикновен смесен номер със знаменател, кратен на 10. Единственото изключение са фракциите без целочислени стойности, след което при четене трябва да се произнесе "нула цели числа".

Например, 45/1000 трябва да се произнася като четиридесет и пет хилядни , докато 0.045 ще звучи като нулева точка четиридесет и пет хилядни .

Смесено число с целочислена част, равна на 7 и фракция 17/100, която е записана като 7.17, и в двата случая ще се чете като седем седемнадесет стотни .

Ролята на заустванията във фракции

Вярно е да се отбележи освобождаването от отговорност - това е, което изисква математика. Десетичните дроби и тяхната стойност могат да се променят значително, ако напишете номера на грешното място. Това обаче беше вярно и преди.

За да прочетете цифрите на целочислената част от десетичната запетая, просто трябва да използвате правилата, известни за естествените числа. А от дясната страна те се отразяват и четат по различен начин. Ако в цялата част "звучат десетки", то след запетая ще бъде вече "десети".

Ясно е, че това може да се види в тази таблица.

Как да напиша смесен номер в десетичната?

Ако знаменателят е число, равно на 10 или 100, а други, тогава въпросът за това как да се преобразува дроб до десетичен, е прост. За да направите това, достатъчно е да пренапишете всичките му съставни части по различен начин. Това ще помогне на следните точки:

• малко настрана, за да напише числителя на фракцията, в този момент десетичната точка е вдясно, след последната цифра;

• преместете запетаята наляво, най-важното тук е да преброите правилно числата - трябва да го преместите до толкова позиции, колкото са нулите в знаменателя;

• ако липсват, тогава празните позиции трябва да са нули;

• нули, които са били в края на числителя, вече не са необходими и могат да бъдат зачертани;

• Преди запетая да се припише целочислената част, ако не беше, тогава ще има и нула.

Предупреждение. Не можете да пресечете нулите, които са били заобиколени от други числа.

Как да бъдем в ситуация, когато номерът в знаменателя е не само от една и нула, как да се преобразува фракцията до десетичната, можете да прочетете малко по-долу. Това е важна информация, която определено трябва да прочетете.

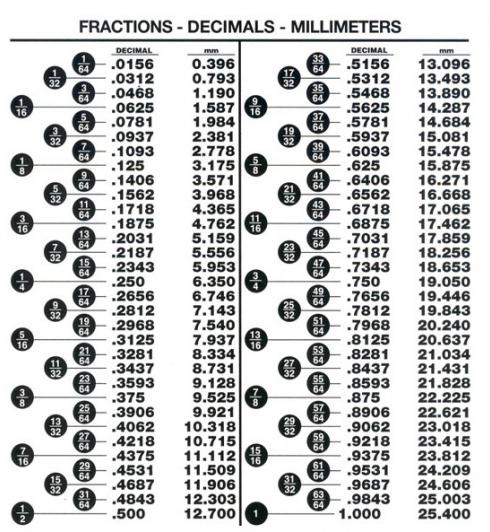
Как да конвертирате дроб до десетичен, ако знаменателят е произволен номер?

Тук има две възможности:

1. Когато знаменателят може да бъде представен като число, което е десет на всяка степен.

2. Ако такава операция не може да се направи.

Как да го проверя? Необходимо е да се разшири знаменателят във фактори. Ако само 2 и 5 присъстват в продукта, тогава всичко е добре и фракцията може лесно да бъде преобразувана в крайния десетичен знак. В противен случай, ако се появят 3, 7 и други прости числа тогава резултатът ще бъде безкраен. Такива десетични дроби за по-лесно използване при математически операции обикновено са закръглени. Това ще бъде обсъдено по-долу.

Проучва как се получават тези десетични дроби, степен 5. Примери тук ще бъдат много полезни.

Нека знаменателите са числа: 40, 24 и 75. Декомпозирането им в основни фактори ще бъде:

• 40 = 2 · 2 · 2 · 5;
• 24 = 2 · 2 · 2;
• 75 = 5 · 5,3.

В тези примери само първата фракция може да бъде представена като краен.

Алгоритъм за преобразуване на обикновена фракция в крайната десетична

• Проверете разширяването на знаменателя в основни фактори и се уверете, че той ще се състои от 2 и 5.

• Добавете към тези числа до 2 и 5, така че те да станат равен брой. Те ще дадат стойността на допълнителния фактор.

• За да умножите знаменателя и числителя с този номер. Резултатът е обикновена фракция, под чиято граница е 10 до известна степен.

• Продължете да действате, както е описано в параграф, разположен малко по-високо.

Ако в задачата тези действия се изпълняват със смесен номер, тогава първо трябва да се представи като грешна фракция. И само тогава действайте по описания сценарий.

Представяне на обща фракция под формата на закръглена десетична запетая

Този начин на преобразуване на една дроб до десетична, ще изглежда още по-лесно за някого. Защото няма голям брой действия. Необходимо е само да се раздели стойността на числителя с знаменателя.

За всяко число с десетична част вдясно от запетая, можете да зададете безкраен брой нули. Този имот трябва да се използва.

Първо напишете цялата част и след нея поставете запетая. Ако фракцията е правилна, напишете нула.

След това е необходимо да се раздели числителя с знаменателя. Така че броят на цифрите, които имат, е един и същ. Това означава, че добавете необходимия брой нули вдясно от числителя.

изпълнява разделяне с бар до необходимия брой цифри. Например, ако трябва да заобиколите до стотни, тогава в отговора трябва да има 3. Като цяло, трябва да има още една цифра, отколкото трябва да получите в края.

Запишете междинния отговор след запетаята и закръглете го в съответствие с правилата. Ако последната цифра е от 0 до 4, тогава просто трябва да я пуснете. А когато тя е равна на 5-9, тогава тя трябва да бъде увеличена с една, отхвърляйки последната.

Връщане от десетичната дроб до обикновена

В математиката има проблеми, когато десетичните дроби са по-удобно представени като обикновени, в които има числител с знаменател. Можете да въздъхнете с облекчение: тази операция винаги е възможна.

За тази процедура направете следното:

• напишете целочислената част, ако е нула, тогава не е нужно да пишете нищо;

• начертайте линия;

• над него се записват числата от дясната страна, ако първите са нули, тогава те трябва да бъдат зачертани;

• под реда напишете единица с толкова нули, колкото е броят на цифрите след десетичната точка в началната фракция.

Това е всичко, което трябва да направите, за да преобразувате десетичната дроб в обикновена.

Какво може да се направи с десетични дроби?

В математиката това са определени действия с десетични дроби, които преди това са били извършвани за други числа.

Те са:

• сравнение;

• събиране и изваждане;

• умножение и разделяне.

Първото действие, сравнение, е подобно на начина, по който е направено за естествените числа. За да определите коя е по-голяма, трябва да сравните изхвърлянията на цялата част. Ако те се окажат равни, те отиват на частични и също ги сравняват по цифри. Този брой, където ще има голяма фигура в старшата категория, също ще бъде отговорът.

Добавяне и изваждане на десетични дроби

Това е може би най-простите действия. Защото те следват правилата за естествените числа.

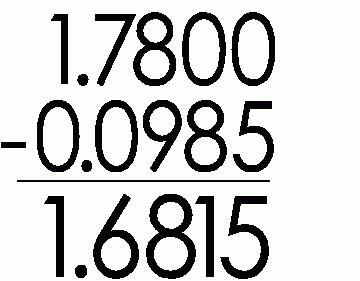
Така че, за да извършите добавянето на десетични дроби, те трябва да бъдат написани една след друга, поставяйки запетаи в колона. С такова влизане вляво от запетаите са цели части, а отдясно - частични. И сега трябва да добавите числата един по един, както е направено с естествени числа, отпадане на запетая. Необходимо е да се започне добавяне от най-малката категория на дробната част на числото. Ако дясната половина няма достатъчно номера, добавете нули.

Когато се изважда, действайте същото. И тук е правилото, което описва способността да се вземе единица от висшето ниво. Ако десетичната дроб има по-малко цифри от приспадащата, то тогава нули се присвояват просто на нея.

Малко по-сложно е случаят с задачи, при които трябва да извършите умножение и деление на десетични дроби.

Как да се умножи десетичната дроб в различни примери?

Правилото, с което се прави умножение на десетични дроби с естествено число, е:

• напишете ги в колона, без да обръщате внимание на запетая;

• да се размножават като естествени;

• отделни запетаи с толкова цифри, колкото са били в дробната част на оригиналния номер.

Специален случай е пример, в който естественото число е 10 до всяка степен. След това, за да получите отговора, просто трябва да преместите запетая в дясно в толкова позиции, колкото има нули в другия множител. С други думи, когато се умножи по 10, запетаите се изместват с една цифра, с 100 - ще има две от тях, и така нататък. Ако в дробната част няма достатъчно цифри, тогава трябва да напишете нули на празни позиции.

Правилото, което се използва, когато в задачата трябва да се умножат десетичните дроби с друг същия номер:

• пишете ги един под друг, без да обръщате внимание на запетаи;

• да се размножават като естествени;

• отделни запетаи с толкова цифри, колкото и в дробните части на двете оригинални части.

Специален случай са примерите, при които един от факторите е равен на 0.1 или 0.01 и повече. Те трябва да преместват запетаята наляво по броя на цифрите в представените множители. Това означава, че ако се умножи по 0.1, тогава запетая се измества с една позиция.

Как да разделим десетичната запетая в различни задачи?

Разделянето на десетични дроби на естествено число се извършва съгласно следното правило:

• напишете ги за разделяне в бар, като че ли са естествени;

• да се разделят според обичайното правило до приключване на цялата част;

• поставете запетая в отговор;

• продължи да се раздели фракционният компонент до достигане на нула в останалата част;

• ако е необходимо, можете да зададете необходимия брой нули.

Ако целочислената част е нула, тогава и тя няма да бъде в отговора.

Отделно има деление на числа, равно на десет, сто и т.н. В такива задачи трябва да преместите запетаята наляво от броя на нулите в разделителя. Случва се, че в целочислената част няма достатъчно цифри, вместо това се използват нули. Можете да видите, че тази операция е подобна на умножение с 0.1 и числа, подобни на нея.

За да изпълнявате десетични дроби, трябва да използвате това правило:

• превърнете делителя в естествено число и за тази цел преместете запетая в него надясно до края;

• премествайте запетая и в дивидента със същия брой цифри;

• действие по предишния сценарий.

Откройте се деление с 0.1; 0.01 и други подобни номера. В такива примери запетая се измества надясно с броя на цифрите в дробната част. Ако са приключили, трябва да добавите липсващия брой нули. Заслужава да се отбележи, че това действие повтаря делението на 10 и подобни числа.

Заключение: всичко се отнася до практиката

Нищо в училище не е лесно и без усилие. За надеждното разработване на нови материали е необходимо време и обучение. Математиката не е изключение.

Така че темата за десетичните дроби не предизвиква трудности, трябва да решите примери с тях колкото е възможно повече. В крайна сметка, имаше време, когато добавянето на естествени числа обърка. И сега всичко е наред.

Ето защо, за да перифразираме една добре позната фраза: решавате, решавате и решавате отново. Тогава задачите с такива номера ще се изпълняват лесно и естествено, като друг пъзел.

Между другото, пъзелите първоначално са трудни за решаване и тогава трябва да направите познати движения. Същото е и в математическите примери: след няколко пъти по един път, вече няма да мислите къде да се обърнете.