Разделяне с нула. Очарователна математика

Числото 0 може да бъде представено като вид граница, разделяща света на реалните числа от въображаеми или отрицателни. Поради неясната позиция много операции с тази цифрова стойност не подлежат на математическа логика. Невъзможността за разделяне с нула е ярък пример. А разрешените аритметични операции с нула могат да бъдат изпълнени, като се използват общоприетите определения.

История на нула

Нула е отправна точка във всички стандартни системи за смятане. Европейците започнаха да използват този брой сравнително скоро, но мъдреците Древна Индия използва нула в продължение на хиляда години, преди празният номер да се използва редовно от европейските математици. Дори преди индианците, нула беше задължително количество в числовата система на Мая. Този американски народ е използвал дуоденалното смятане и с нула те започват на първия ден от всеки месец. Интересно е, че в Мая знакът „нула“ съвпада напълно със знака, определящ „безкрайност“. По този начин древните маи заключават, че тези количества са идентични и непознаваеми.

Математически операции с нула

Стандартните математически операции с нула могат да бъдат сведени до няколко правила.

Допълнение: ако към произволно число се добави нула, тя няма да промени стойността му (0 + x = x).

Изваждане: при изваждане на нула от произволно число, стойността на изваденото остава непроменена (x-0 = x).

Умножение: всяко число, умножено по 0, дава 0 в продукта (a * 0 = 0).

Разделение: нула може да се раздели на всяко число, което не е равно на нула. В този случай стойността на такава фракция ще бъде 0. И разделянето с нула е забранено.

Степенуване. Това действие може да се извърши с произволен брой. Произволно число, повдигнато до нулева степен, ще даде 1 (x ⁰ = 1).

Нула е 0 до всяка степен (0 ^a = 0).

В този случай веднага възниква противоречие: изразът 0 ⁰ няма смисъл.

Парадокси на математиката

Фактът, че разделението на нула е невъзможно, много хора знаят от училище. Но по някаква причина е невъзможно да се обясни причината за такава забрана. Всъщност защо формулата за разделяне с нула не съществува, но други действия с този брой са доста разумни и възможни? Отговорът на този въпрос е даден от математиците.

Работата е там, че обичайните аритметични операции, които учениците учат в началното училище, всъщност далеч не са равни в правата, както ни се струва. Всички прости операции с числа могат да бъдат намалени до две: добавяне и умножение. Тези действия представляват същността на самото понятие за число, докато останалите операции се основават на използването на тези две.

Добавяне и умножение

Вземете стандартния пример за изваждане: 10-2 = 8. В училище се смята просто: ако от десет точки се отнемат две позиции, осем ще останат. Но математиците разглеждат тази операция по съвсем различен начин. В крайна сметка такава операция като изваждане не съществува за тях. Този пример може да бъде написан по друг начин: x + 2 = 10. За математиците неизвестната разлика е само номер което трябва да се добави към две, за да се направи осем. И не се изисква изваждане тук, просто трябва да намерите подходящата цифрова стойност.

Умножението и делението се считат за еднакви. В Пример 12: 4 = 3 може да се разбере, че става въпрос за разделяне на осем обекта на две равни групи. Но в действителност това е просто обърната формула на записа 3x4 = 12. Такива примери за разделение могат да се дават безкрайно.

Примери за разделяне с 0

Тук става малко ясно защо е невъзможно да се раздели с нула. Умножението и делението с нула се подчиняват на собствените си правила. Всички примери за разделянето на това количество могат да бъдат формулирани като 6: 0 = x. Но това е обърнат запис на израза 6 * x = 0. Но, както знаете, всяко число, умножено по 0, дава само 0 в продукта, което е присъщо на самата концепция за нулева стойност.

Оказва се, че няма такъв номер, който, умножен по 0, дава някаква осезаема стойност, т.е. тази задача няма решение. Този отговор не трябва да се страхува, това е естествен отговор за задачи от този тип. Самото писане 6: 0 няма смисъл и тя не може да обясни нищо. Накратко, този израз може да се обясни с безсмъртното „разделяне с нула е невъзможно”.

Има ли операция 0: 0? Всъщност, ако операцията по умножение с 0 е законна, може ли да бъде разделена на нула? В крайна сметка уравнението на формата 0x 5 = 0 е напълно законно. Вместо номер 5, можете да поставите 0, продуктът от това няма да се промени.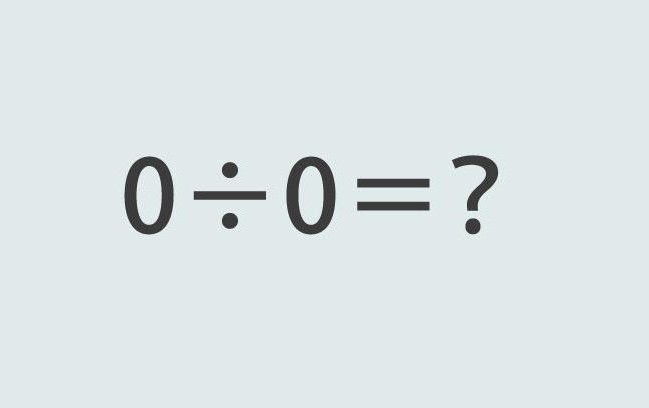

Всъщност 0x0 = 0. Но все още е невъзможно да се разделят с 0. Както бе споменато, разделението е просто обратното умножение. Така, ако в примера 0x5 = 0, трябва да определим втория фактор, получаваме 0x0 = 5. Или 10. Или безкрайност. Разделяйки безкрайността с нула - как ви харесва?

Но ако някой брой се впише в израза, тогава няма смисъл, не можем да изберем едно от безкрайно множество от числа. И ако е така, това означава, че изразът 0: 0 няма смисъл. Оказва се, че дори и самата нула не може да бъде разделена на нула.

Висша математика

Разделянето с нула е главоболие за училищната математика. Учи в технически университети математически анализ леко разширява концепцията за задачи, които нямат решение. Например към вече известния израз 0: 0 добавят се нови, които нямат решение в училищните математически курсове:

• безкрайност, разделена на безкрайност: ∞: ∞;
• безкрайност минус безкрайност: ∞ - ∞;
• единица, издигната до безкрайна мощност: 1 ^∞ ;
• безкрайност, умножена по 0: 0 * 0;
• някои други.

Елементарни методи за решаване на такива изрази е невъзможно. Но по-високата математика, поради допълнителни възможности за редица подобни примери, дава окончателни решения. Това е особено очевидно при разглеждането на проблемите от теорията на границите.

Разкриване на несигурност

В теорията на границите стойността 0 се заменя с условна безкрайно малка променлива. И изразите, в които се получава разделяне с нула чрез заместване на желаната стойност, се преобразуват. По-долу е представен стандартен пример за разкриването на лимита с помощта на обикновени алгебрични трансформации:

Както може да се види в примера, простото намаляване на фракцията води до неговата стойност до напълно рационален отговор.

Когато се разглеждат границите на тригонометричните функции, техните изрази са склонни да бъдат сведени до първата забележителна граница. При разглеждане на границите, при които знаменателят се превръща в 0 при определяне на лимита, използвайте втория забележителен лимит.

L'Hôpital метод

В някои случаи границите на изразите могат да бъдат заменени с границата на техните производни. Гийом Лопитал - френски математик, основател на френското училище по математически анализ. Той доказа, че границите на изразите са равни на границите на дериватите на тези изрази. В математическото писане неговото правило е следното.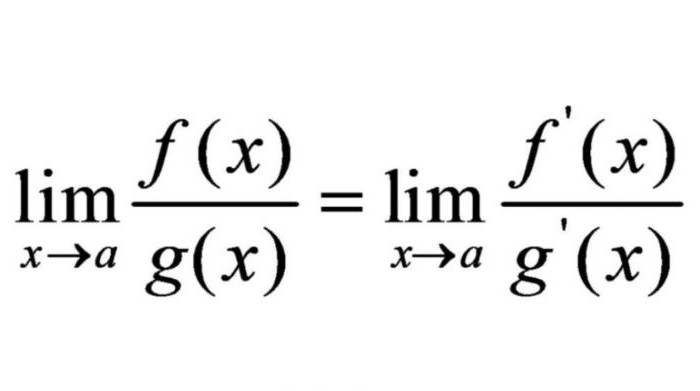

Понастоящем методът L'Hôpital се използва успешно при решаването на несигурности от типа 0: 0 или ∞: ∞.