Корелационен коефициент и причинно-следствена връзка: формули и тяхната интерпретация

Коефициентът на корелация е степента на връзка между две променливи. Неговото изчисление дава представа дали има зависимост между два масива от данни. За разлика от регресията, корелацията не позволява да се предскажат стойностите на количествата. Изчисляването на коефициента обаче е важна стъпка в предварителния статистически анализ. Например, установихме, че коефициентът на корелация между нивото на преките чуждестранни инвестиции и темповете на растеж на БВП е висок. Това ни дава представа, че за да се осигури благосъстояние, е необходимо да се създаде благоприятен климат за чуждестранните предприемачи. Не е толкова очевидно заключение на пръв поглед!

Корелация и причинност

Може би няма нито една област от статистиката, която да е толкова твърдо установена в нашия живот. Коефициентът на корелация се използва във всички области на общественото познание. Основната му опасност се състои в това, че високите му ценности често се спекулират, за да убедят хората и да ги накарат да вярват в някои заключения. В действителност обаче силната корелация изобщо не показва причинно-следствена връзка между количествата.

Коефициент на корелация: формула Pearson и Spearman

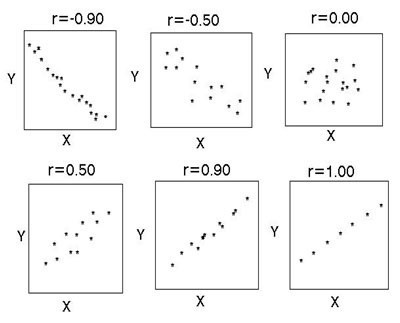
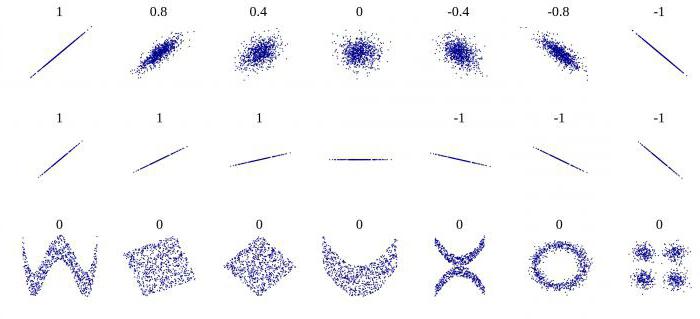
Има няколко ключови индикатора, които характеризират връзката между две променливи. Исторически, първият е линейният корелационен коефициент на Пиърсън. Той все още е в училище. Тя е разработена от К. Пиърсън и Й. Юл въз основа на творбите на о. Галтън. Този коефициент ви позволява да видите връзката между рационалните числа, които се променят рационално. Той винаги е по-голям от -1 и по-малък от 1. Отрицателното число показва обратна пропорционална зависимост. Ако коефициентът е нула, тогава няма връзка между променливите. Равно на положително число - има пряко пропорционална връзка между изследваните количества. Коефициентът на корелация на Spearman ви позволява да опростите изчисленията чрез изграждане на йерархия от стойности на променливи.

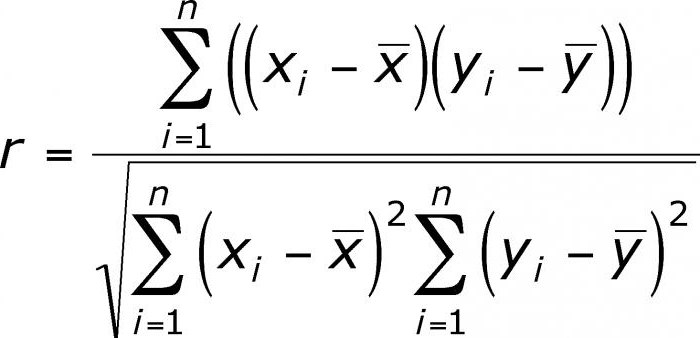
Връзка между променливите

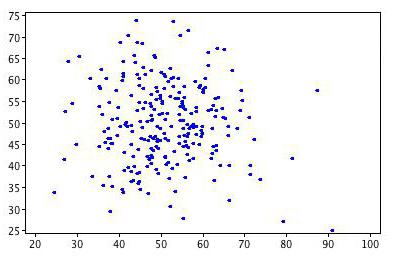
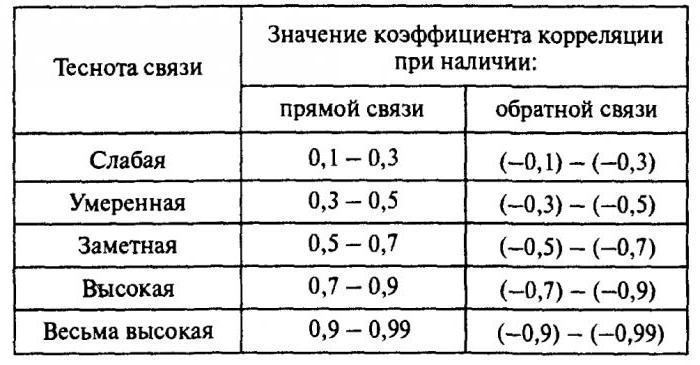
Съотношението помага да се намери отговор на два въпроса. Първо, дали връзката между променливите е положителна или отрицателна. Второ, колко силна е зависимостта. Корелационен анализ е мощен инструмент, чрез който можете да получите тази важна информация. Лесно е да се види, че приходите и разходите на семейството спадат и растат пропорционално. Тази връзка се счита за положителна. Напротив, с нарастването на цените на стоките търсенето за него пада. Такава връзка се нарича отрицателна. Стойностите на коефициента на корелация са в интервала между -1 и 1. Нула означава, че няма връзка между изследваните стойности. Колкото по-близо е индикаторът до крайните стойности, толкова по-силна е връзката (отрицателна или положителна). Отсъствието на зависимост се посочва с коефициент от -0.1 до 0.1. Необходимо е да се разбере, че такава стойност показва само липсата на линейна връзка.

Функции на приложението

Използването на двата показателя зависи от определени предположения. Първо, наличието на силна връзка не означава, че едно количество определя друго. Може да има и трето количество, което определя всяко едно от тях. Второ, високият коефициент на корелация на Pearson не показва причинно-следствена връзка между изследваните променливи. Трето, тя показва само линейна зависимост. Корелацията може да се използва за оценка на значими количествени данни (например атмосферно налягане, температура на въздуха), а не категории като пол или любим цвят.

Коефициент на множествена корелация

Pearson и Spearman изследват връзката между двете променливи. Но как да действа в случай, че има три или дори повече. Тук спасява коефициентът на множествена корелация. Например, брутният национален продукт не се влияе само от преките чуждестранни инвестиции но също и парични и фискална политика както и равнището на износа. Темпът на растеж и обемът на БВП са резултат от взаимодействието на редица фактори. Въпреки това, трябва да се разбере, че моделът на множествената корелация се основава на редица опростявания и предположения. Първо, изключва се мултиколинеарността между количествата. Второ, връзката между зависимата и променливата, които я засягат, се приема за линейна.

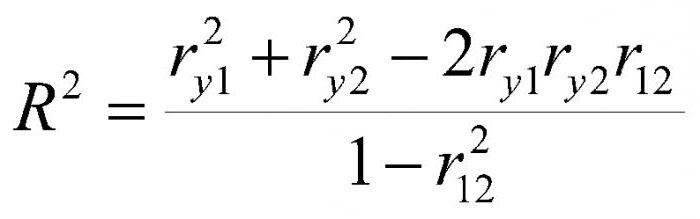
Области на използване на корелационен и регресионен анализ

Този метод за намиране на връзката между количествата се използва широко в статистиката. Най-често се използва в три основни случая:

1. За да се тества причинно-следствената връзка между стойностите на две променливи. В резултат на това изследователят се надява да намери линейна връзка и да извлече формула, която описва тези връзки между количествата. Единиците на техните измервания могат да бъдат различни.
2. За да проверите връзката между стойностите. В този случай никой не определя коя променлива зависи. Може да се окаже, че стойността на двете величини причинява друг фактор.
3. За извличане на уравнението. В този случай можете просто да замените числата в него и да откриете стойностите на неизвестната променлива.

Човек търси причинно-следствена връзка

Съзнанието е подредено по такъв начин, че определено трябва да обясним събитията, които се случват наоколо. Човек винаги търси връзка между картината на света, в който живее, и информацията, която получава. Често мозъкът създава ред от хаос. Той лесно може да види причинно-следствената връзка там, където няма такава. Учените трябва специално да се научат да преодоляват тази тенденция. Способността за оценка на връзката между данните е обективно необходима в академична кариера.

Пристрастие към медиите

Помислете как наличието на корелационна връзка може да бъде погрешно интерпретирано. Група британски студенти с лошо поведение бяха запитани дали родителите им пушат. След това тестът беше публикуван във вестника. Резултатът показа силна връзка между пушенето на родителите и престъпленията на децата им. Професорът, който провеждаше проучването, дори предложи да постави предупреждение на опаковките на цигарите. Съществуват обаче редица проблеми с това заключение. Първо, корелацията не показва коя от количествата е независима. Следователно може да се предположи, че пристрастяването на родителите е причинено от неподчинението на децата. Второ, не е възможно да се каже със сигурност, че и двата проблема не се появяват поради някакъв трети фактор. Например семействата с ниски доходи. Трябва да се отбележи емоционалният аспект на първоначалните констатации на професора, който е провел изследването. Той беше пламенен противник на пушенето. Затова не е изненадващо, че той интерпретира резултатите от изследванията си по този начин.

данни

Неправилното тълкуване на корелацията като причинно-следствена връзка между две променливи може да доведе до срамни грешки в изследванията. Проблемът е, че той лежи в самата същност на човешкото съзнание. Много маркетингови трикове са изградени върху тази конкретна функция. Разбирането на разликата между причинно-следствената връзка и взаимовръзката ви позволява рационално да анализирате информацията в ежедневието и в професионалната си кариера.