Какво е името на четириъгълника с прави ъгли?

Изследването на геометрията започва с разглеждане на прости фигури в равнината, които лесно могат да се представят чрез абстрактно въображение. Една от тези фигури е четириъгълник с прави ъгли. В 3-ти клас на общообразователните училища те започват да се запознават с него и да проучват подробно неговите свойства в горните класове. Разгледайте основните характеристики на тази фигура в статията, както и примери за нейното използване в ежедневието.

Какво е името на четириъгълник с прави ъгли?

Думата "четириъгълник" казва, че въпросната фигура се състои от четири ъгъла. В самолет ще бъде затворен само ако има четири прави страни. Ако противоположните страни са успоредни една на друга по двойки, тогава такава фигура се нарича паралелограма. Четирите ъгъла са равни по двойки, но могат да приемат произволни стойности от 0 до 180 ^o . Ако всичките му ъгли са равни на 90 ^о , тогава те се наричат ​​прави. Четириъгълник с прави ъгли е правоъгълник и в същото време е успоредник.

Правоъгълникът се характеризира само с два параметъра: дължините на съседните страни. По-нататък в статията ще ги обозначим с a и b. Ако тези дължини са еднакви, то правоъгълникът се дегенерира в квадрат.

Квадратна формула

Правоъгълникът е перфектна фигура, към която човек по време на своята житейска дейност се опитва да постави околните предмети, например тухла, формата на двора пред къща, компютърен монитор и т.н. Следователно, често съществува проблем при изчисляването на площта на правоъгълник.

Изчислете площта на въпросната цифра не е трудно. Тъй като правоъгълникът е успоредник, неговата площ се изчислява като произведение от две дължини: височината, спусната от едната страна и тази страна. Височината на успоредника се намира като произведение на синуса на единия от ъглите му и неговата страна. Тъй като разглеждаме конкретен вид успоредник - правоъгълник, синусът на десния ъгъл е равен на единица, което означава, че търсената формула за областта приема следната форма:

S = a * b

Площта на четириъгълника с прав ъгъл е равна на произведението на дължините на двете му непаралелни страни.

По-долу ще бъде показано как да се намери площта на правоъгълника, ако другите му елементи са известни, например дължината на диагонала.

Диагонален правоъгълник

Фигурата по-долу показва произволен четириъгълник с прави ъгли и двете му диагонали.

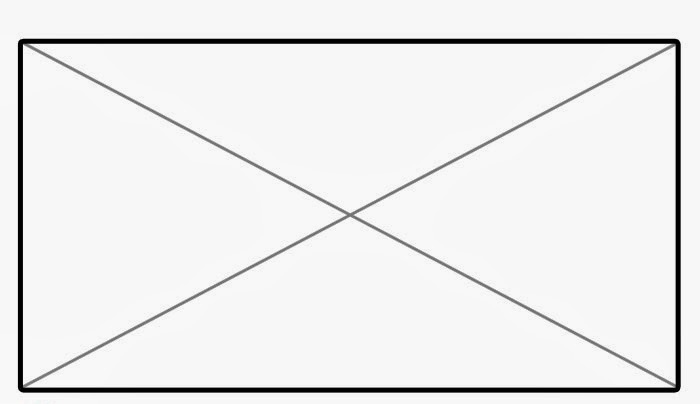
Вижда се, че диагоналите разделят на две части противоположните прави ъгли на фигурата. Ще обозначим точката на пресичане на диагоналите със символа C. Това е важно, защото е център на симетрия на фигурата. Дължините на двете диагонали са равни.

Диагоналите разделят правоъгълника на четири равнобедрени триъгълника, за които лесно се изчисляват дължините на страните и областта. Всеки два триъгълника, чиито бази лежат на страни с еднаква дължина на правоъгълник, са едни и същи.

Ако държите един диагонал, той ще раздели правоъгълника на два абсолютно еднакви прави триъгълника. Този факт ви позволява да използвате Pythagorean thiorem за изчисляване на диагоналната дължина, познавайки краката на триъгълника. Фигурата по-долу показва как да намерите квадрата на диагонала c на правоъгълника. Тук диагоналът е хипотенузата, а страните на правоъгълника съответстват на краката на триъгълника.

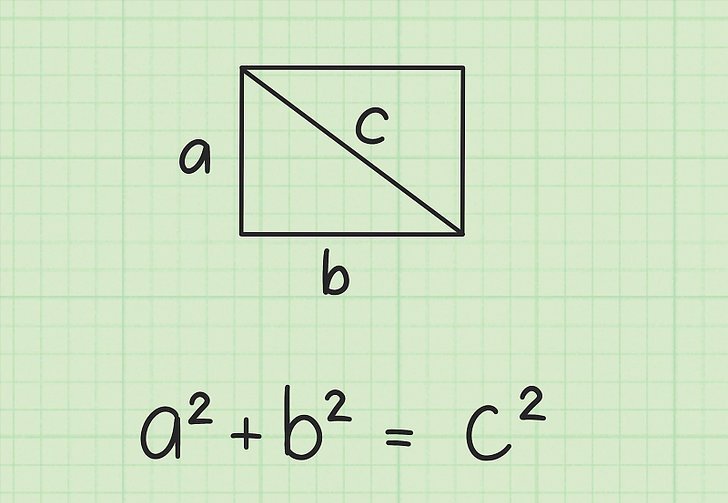
Тогава стойността на дължината c ще бъде равна на:

c = √ (a ² + b ² )

Правоъгълник на симетрията

Както беше отбелязано, центърът на неговата симетрия е точката С, образувана от пресичащи се диагонали. Като се има предвид фигурата в равнината, можем да кажем, че оста, минаваща през тази точка и успоредна на две страни на правоъгълника, е оста на симетрия на втория ред, т.е. обръщане около 180 ^{° ще} превърне правоъгълника в себе си. Тъй като разглежданият четириъгълник има две двойки успоредни страни, очевидно е, че той има две определени оси на симетрия.

Оста на симетрия разделя формата на два еднакви правоъгълника със страни:

a и b / 2 или b и a / 2

Някои геометрични свойства на правоъгълник

Тъй като въпросната фигура има определена симетрия, има прави ъгли и двойки паралелни страни, за нея е възможно да се идентифицират редица важни свойства, използвани в практиката. Ние ги изброяваме:

1. Всяка линия, която минава през центъра C на фигурата, се пресича в две точки на същото разстояние от точка C. Максималното разстояние от С до страната на диагонала на правоъгълника е половината от дължината на диагонала, минималното разстояние е равно на половината от дължината на късата му страна.
2. Ако разделим едната страна на правоъгълника наполовина, след това свързвайки тази точка с върховете на противоположната паралелна страна, получаваме равнобедрен триъгълник с площ, равна на половината от площта на правоъгълника.
3. Ако описаната по-горе точка е изместена от центъра на страната към едната или другата му страна, тогава равновесните части на маркирания триъгълник ще бъдат нарушени, но неговата площ ще остане непроменена.
4. Всеки правоъгълник може да бъде въведен в кръг.

Първото свойство е очевидно, тъй като всяка права линия, преминаваща през С, ще пресича паралелните страни на формата. Доказваме останалите свойства.

Доказателство за свойства 2, 3 и 4

Първо ще разгледаме свойства 2 и 3. Фигурата по-долу показва правоъгълник с три триъгълника от двете страни:

ABC ₁ , ABC ₂ и ABC ₃

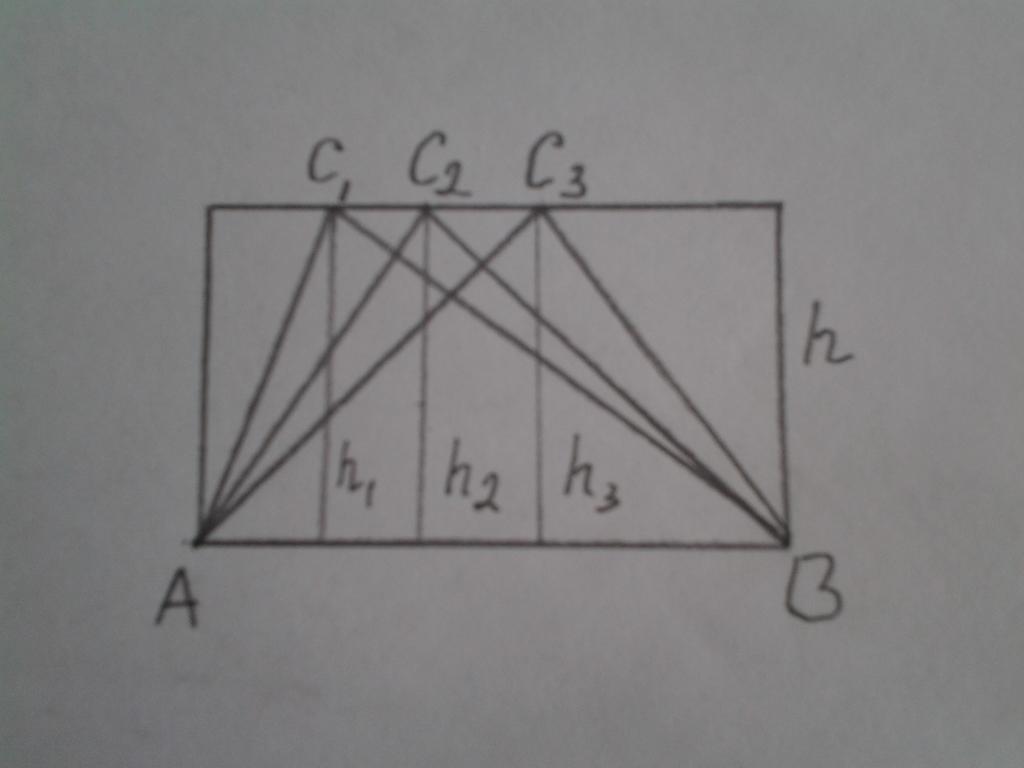
Съгласно формулата за намиране на площта на триъгълник, за тях може да се напише:

S ₁ = 1/2 * h ₁ * AB;

S2 = 1/2 * h ₂ * AB;

S ₃ = 1/2 * h ₃ * AB

Може да се види, че всички височини h _{i на} разглежданите триъгълници са равни на дължината на страната h на правоъгълника. Това означава, че техните области са равни:

S1 = S2 = S3

Сега ще напишем формулата за областта S на правоъгълника и ще разделим S с площта на един от изобразените триъгълници, получаваме:

S = AB * h;

S / S ₁ = AB * h / (1/2 * h * AB) = 2

По този начин правоъгълникът има площ два пъти по-голяма от която и да е от изобразените триъгълници, т.е. доказахме втората и третата свойства.

Що се отнася до възможността за вписване на четириъгълник с прав ъгъл в кръг, тук е необходимо да се спори по следния начин: рисуваме диагонали на фигурата, те се пресичат в точка С. Тъй като тази точка е на същото разстояние от четирите върха на правоъгълника, тя може да служи като център на кръга. Ако радиусът на окръжността е равен на половината от дължината на диагонала, тогава кръговата линия ще премине през всичките четири върха на правоъгълника, тоест ще бъде вписана в нея.

Четириъгълник ли е с един ъгъл, правоъгълник?

Отговорът на въпроса ще бъде положителен само ако въпросният четириъгълник е успоредник. В този случай, ако един ъгъл е равен на 90 ^° , тогава другите два съседни ъгъла също ще бъдат прави, което означава, че четвъртият ъгъл също ще бъде равен на 90 ^° . Открихме правилните ъгли в четириъгълника всичко, което означава, че е правоъгълник.

Ако четириъгълник с един прав ъгъл няма двойки паралелни страни, то той няма да бъде правоъгълник.

Къде се използва правоъгълникът и неговите свойства?

При производството на тетрадни листове се използва правоъгълна форма и съотношението на дължините на по-голямата страна към по-малката е .2. Тази форма на фигурата води до факта, че ако е разделена наполовина от симетрична ос, успоредна на по-голямата страна, тогава двете образувани нови правоъгълници ще имат аспектно съотношение от .2. Такова разделение може да продължи до безкрайност, докато формата на получените правоъгълници ще се запази.

Правоъгълната форма се използва при производството на телевизионни екрани. Преди ерата на течнокристалните (LCD) монитори се използват електронно-лъчеви екрани, чиято пропорция е равна на 4: 3. С появата на LCD монитори с висока резолюция, те започнаха да прилагат новия стандарт: 16: 9.

Мозайката, която украсява стените на сградите, също има формата на четириъгълник с прави ъгли.

Изчисляване на площта на фигурата по известния диагонал

Завършваме статията, като разглеждаме въпроса за изчисляване на площта на четириъгълника, чиито върхове на прави ъгли са свързани с диагонал. Изчислете площта на модерен LCD монитор, ако е известно, че диагоналът му е c = 35 cm.

Този проблем може да бъде решен, защото мониторът има стандартизирано съотношение 16: 9. Обозначавайки с x неизвестен коефициент, получаваме дължините на страните на монитора:

a = 16 * x;

b = 9 * x

Сега прилагаме формулата, за да определим диагонала, получаваме:

c ² = a ² + b ² =>

35 ² = x ² * (16 ^{2 +} 9 ² ) =>

x = 35 / √ (16 ^{2 +} 9 ² ) ≈ 1.9

Тогава страните на монитора и неговата област са равни:

а = 16 х х = 30.4 см;

b = 9 x x = 17.1 cm;

S = a * b ≈ 520 cm ²

Отбелязваме още веднъж, че площта може да бъде определена от стойността на диагонала само ако е известно съотношението на страните на правоъгълника.