Какво е интеграл? Интеграли с подробно решение. Интегрална маса
Думата "интеграл" идва от латинската integralis - холистична. Този дял е предложен през 17-ти век. ученик на великия Лайбниц (а също и изключителен математик) И. Бернули. И какво е интеграл в съвременния смисъл? По-долу ще се опитаме да дадем изчерпателен отговор на този въпрос.
Исторически контекст на понятието интеграл
В началото на 17 век при разглеждането на водещи учени имаше голям брой физически (предимно механични) задачи, при които беше необходимо да се изследват зависимостите на някои количества от други. Най-очевидните и неотложни проблеми бяха определянето на моментната скорост на неравномерно движение на тялото във всеки даден момент и неговия обратен проблем за намиране на величината на пътя, пропътуван от тялото през определен период от време по време на такова движение. Днес вече знаем какъв е интегралът на скоростта на движение - това е пътят, който е изминал. Но разбирането как да го изчислим, познавайки скоростта във всеки момент във времето, не се появи веднага.
На първо място, от разглеждането на такива зависимости на физични величини, например пътя на скоростта, се формира математическата концепция на функцията y = f (x). Изследването на свойствата на различните функции доведе до появата на математически анализ. Учените активно търсят начини за изучаване на свойствата на различните функции. 
Как изчисляването на интеграли и производни?
След като Декарт създаде основите на аналитичната геометрия и възможността да изобрази функционалните зависимости графично по осите на декартова координатна система, изследователите се сблъскаха с две големи нови задачи: как да начертаят допирателна към крива линия във всяка точка и как да се намери площта на фигурата, ограничена над тази крива и прави линии, успоредни на координатните оси. По неочакван начин се оказа, че първата е еквивалентна на намирането на моментната скорост, а втората - на намирането на изминатото разстояние. В крайна сметка, в случай на неравномерно движение, той е изобразен в декартовите оси на координатите „разстояние“ и „време“ с определена крива линия.
Гений Лейбниц и Нютон в средата на 17-ти век. създадени са методи, които позволяват решаването на двата проблема. Оказа се, че за да се проведе допирателна към крива в дадена точка, е необходимо да се намери стойността на така наречената производна на функцията, описваща тази крива в нейната точка, и тази стойност е равна на скоростта на промяна на функцията, т.е. незабавна скорост на тялото.
За да се намери площта, ограничена от крива, е необходимо да се изчисли определен интеграл, който даде точната му стойност. Дериват и интеграл - основните понятия за диференциално и интегрално смятане, които са в основата на съвременния математически анализ - най-важната част от висшата математика.
Площ под кривата
И така, как да го дефинираме точната стойност? Да се опитаме да разкрием процеса на неговото изчисление чрез интеграл в детайли, от самото начало.
Нека f е непрекъсната функция на интервала [ab]. Разгледайте кривата y = f (x), показана на фигурата по-долу. Как да се намери площта, ограничена от кривата), ос x, и редовете x = a и x = b? Това е областта на засенчената фигура на фигурата. 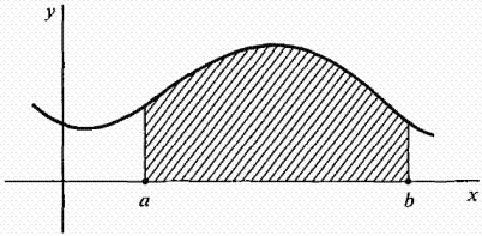
Най-простият случай е, когато f е постоянна функция; кривата е хоризонталната линия f (X) = k, където k е константа и k ≥ 0, както е показано на фигурата по-долу. 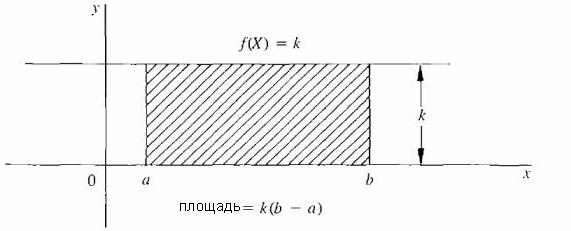 В този случай площта под кривата е просто правоъгълник с височина k и ширина (b - a), така че площта се определя като: k · (b - a).
В този случай площта под кривата е просто правоъгълник с височина k и ширина (b - a), така че площта се определя като: k · (b - a).
Областите на някои други прости форми, като триъгълник, трапеция и полукръг, са дадени от планиметрични формули.
Площта под всяка непрекъсната крива y = f (x) се дава от определен интеграл, който е записан по същия начин като редовен интеграл.
Сума Риман
Преди да се потопим в подробен отговор на въпроса какво представлява интеграл, нека да подчертаем някои основни идеи.
Първо, площта под кривата се разделя на определен брой n вертикални ивици с достатъчно малка ширина Δx. Освен това, всяка вертикална ивица се заменя с вертикален правоъгълник с височина f (x), ширина Δx и площ f (x) dx. Следващата стъпка е формирането на сумата от площите на всички тези правоъгълници, наречена риманова сума (виж фигурите по-долу).
Чрез изчертаване на нашите правоъгълници widex широк, можем да вземем тяхната височина, равна на стойността на функцията на левия ръб на всяка лента, т.е. кривата ще бъде крайната лява точка на техните горни къси страни Δx ширина. В същото време, в участъка, където функцията расте и кривата му е изпъкнала, всички правоъгълници са под тази крива, т.е. тяхната сума ще бъде със сигурност по-малка от точната стойност на площта под кривата в тази област (виж фигурата по-долу). Този метод на сближаване се нарича ляв. 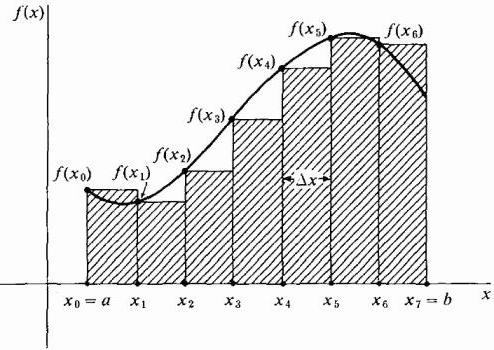
По принцип е възможно да се начертаят апроксимиращи правоъгълници по такъв начин, че крайните десни точки на горните къси страни на ширината Δx лежат върху кривата. Тогава те ще бъдат по-високи от кривата и апроксимацията на площта в тази област ще бъде по-голяма от нейната точна стойност, както е показано на фигурата по-долу. Този метод се нарича правилен. 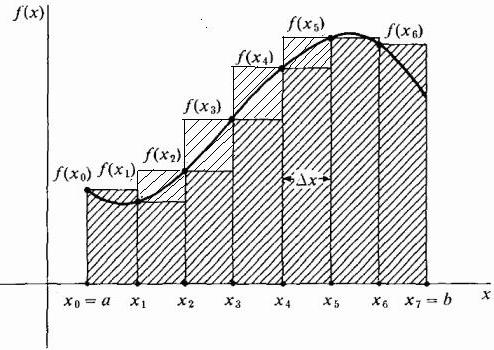
Но също така можем да вземем височината на всеки от апроксимиращите правоъгълници, равна на някаква стойност на функцията в произволна точка x * i в съответната лента Δx i (виж фиг. по-долу). В този случай дори не можем да поемем една и съща ширина на всички ленти. 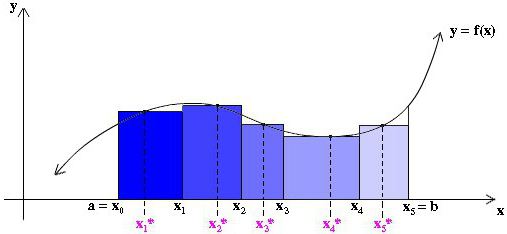
Изчисляваме сумата на Риман:

Преход от сумата на Риман към определен интеграл
В по-висша математика е доказана теорема, която гласи, че ако с неограничено увеличение на числото n на приблизителните правоъгълници, тяхната най-голяма ширина се насочи към нула, тогава римановата сума A n се стреми към някакъв лимит А. Числото А е същото за всеки метод за формиране на апроксимиращи правоъгълници и за всеки избор на точки x * i .
Ясното обяснение на теоремата е дадено на фигурата по-долу.
Това показва, че колкото по-тесни са правоъгълниците, толкова по-близо е областта на стъпаловидната фигура към зоната под кривата. Когато броят на правоъгълниците n → ∞, тяхната ширина е Δx i → 0, а границата А на сумата A n е числено равна на изискваната площ. Това ограничение и има определена интегрална функция f (x): 
Интегралният символ, който е модифициран курсив S, е въведен от Leibniz. J. Б. Фурие предложи да постави нотацията за интеграла в горната и долната му част. В същото време началната и крайната стойност на x са ясно посочени.
Геометрична и механична интерпретация на определен интеграл
Нека се опитаме да дадем подробен отговор на въпроса какво представлява интегралът? Разгледайте интеграла на интервала [a, b] от положителната функция f (x) в него и приемете, че горната граница е по-голяма от по-ниската Ако ординатите на функцията f (x) са отрицателни вътре в [a, b], тогава абсолютната стойност на интеграла е равна на площта между оста x и графа y = f (x), а самата интеграла е отрицателна. В случай на единично или многократно пресичане на оста y = f (x) на абсцисата на сегмент [a, b], както е показано на фигурата по-долу, за изчисляване на интеграла, е необходимо да се определи разликата, при която намалението е равно на общата площ на участъците над x-оста и приспадане - общата площ на площите под нея. Механичната интерпретация на определен интеграл е тясно свързана с геометричната. Нека се върнем към раздела "Riemann sum" и си представете, че графиката, показана на фигурите, изразява функцията на скоростта v = f (t) с неравномерно движение материална точка (Оста на абсцисата е времевата ос). Тогава площта на всеки апроксимиращ правоъгълник с ширина Δt, която сме построили при формирането на римановата сума, ще изрази приблизително пътя на точката по време Δt, а именно v (t *) Δt. Общата сума на площите на правоъгълниците на интервала от t 1 = a до t 2 = b изразява приблизително пътя s за времето t 2 - t 1 и неговата граница, т.е. интегралът (дефиниран) от a до b на функцията v = f (t) над dt ще даде точната стойност на пътя s. Ако се върнем към неговото обозначение, тогава можем да приемем, че a = const и b е специфичната стойност на някаква независима променлива x. Тогава определен интеграл с горна граница x̃ от конкретно число се превръща във функция от x̃. Такъв интеграл е равен на площта на фигурата под кривата, посочена от точки aABb на фигурата по-долу. Да предположим, че сме дали на променливата x̃ = b малко малък прираст ̃x̃. Тогава увеличаването на площта на фигурата aABb се състои от площта на правоъгълника (засенчена на фигурата) Bb ̃ Δx of и площта на фигурата на BDC под кривата. Площта на правоъгълника е равна на Bb x Δx f = f (x̃) Δx̃, т.е. тя е линейна функция на прираста на независимата променлива. Площта на формата на БДК е очевидно по-малка от площта на правоъгълника BDCK = Δx̃ ∙ Δy, и като има тенденция Δx, → 0, тя намалява дори по-бързо от нея. Следователно f (x̃) ̃x̃ = f (x̃) dx̃ е диференциалът на променливата област aABb, т.е. диференциалът на определен интеграл От това можем да заключим, че изчисляването на интегралите се състои в намирането на функциите от дадените изрази на техните диференциали. Интегралното смятане е именно системата от методи за намиране на такива функции от познатите им диференциали. Тя свързва връзката между диференциацията и интеграцията и показва, че съществува операция, обратна на диференциацията на дадена функция - нейната интеграция. Той също така показва, че ако някоя функция f (x) е непрекъсната, тогава чрез прилагане на тази математическа операция към нея можете да намерите цял ансамбъл (набор, набор) от функции примитивни за него (или по друг начин да намерите неопределен интеграл от него). Нека функцията F (x) е обозначението на резултата от интегрирането на функцията f (x). Съответствието между тези две функции в резултат на интегрирането на втората от тях се посочва както следва: Както може да се види, при интегралния символ няма граници за интеграция. Това означава, че от определено тя се трансформира в неопределен интеграл. Думата "неопределен" означава, че резултатът от операцията по интеграция в този случай не е една, а много функции. Всъщност, освен самата функция F (x), всяка функция F (x) + C удовлетворява последните изрази, където C = const. Това означава, че постоянният член на събранието на антидериванти може да бъде определен произволно. Трябва да се подчертае, че ако интегралът, дефиниран от функцията, е число, тогава неопределеното е функция, по-точно, тяхното множество. Терминът "интеграция" се използва за определяне на търсенето на двата типа интеграли. Това е пълната противоположност на съответното правило за диференциация. Как се вземат неопределените интеграли? Примери за тази процедура, ние разглеждаме специфичните функции. Нека разгледаме силовата функция на общата форма: f (x) = cx n След като сме направили това с всеки член в израза на интегриращата функция (ако има няколко), добавяме константа в края. Припомнете си, че като вземете дериват на константна стойност, той го разрушава, така че вземането на интеграл от всяка функция ще ни даде възстановяването на тази константа. Ние го обозначава с С, тъй като константата е неизвестна - тя може да бъде всяко число! Следователно можем да имаме безкрайно много изрази за неопределен интеграл. Нека разгледаме прости неопределени интеграли, примери за които са показани по-долу. Да предположим, че трябва да намерите интеграла на функцията: f (x) = 4x 2 + 2x - 3. Да започнем с първия мандат. Разглеждаме показателя 2 и го увеличаваме с 1, след това разделяме първия член на получения индикатор 3. Получаваме: 4 (x 3 ) / 3. След това разглеждаме следващия член и правим същото. Тъй като има експонентен 1, полученият индикатор ще бъде 2. По този начин разделяме този член на 2: 2 (x 2 ) / 2 = x 2 . Последният член има фактор x, но ние просто не го виждаме. Можем да си представим последния член като (-3x 0 ). Това е еквивалентно на (-3) ∙ (1). Ако използваме правилото за интеграция, добавяме 1 към индикатора, за да го повишим до първа степен, и след това разделяме последния член на 1. Получаваме 3x. Това правило за интеграция работи за всички стойности на n, с изключение на n = - 1 (защото не можем да разделим с 0). Разгледахме най-простия пример за намиране на интеграла. Като цяло, решението на интеграли не е лесна задача, а опитът, придобит по математика, е добра помощ в него. В горния раздел видяхме, че от всяка формула за диференциация се получава съответната интеграционна формула. Следователно всички възможни варианти отдавна са получени и обобщени в съответните таблици. Следващата таблица на интегралите съдържа формули за интегриране на основните алгебрични функции. Тези формули трябва да се помнят, да се запомнят постепенно, тъй като са фиксирани упражнения. Друга таблица с интеграли съдържа основните тригонометрични функции: Оказва се, че за да се постигне това, възможността да се интегрира, т.е. да се намерят неопределени интеграли, е много проста. И формулата на основателите на интегро-диференциалното смятане на Нютон-Лайбниц помага в това. Според него, на първия етап, изчисляването на желания интеграл се състои в намирането на неопределен, след това изчисляване на стойността на намерената примитивна F (x) с заместване на x, равна на горната граница, след това към по-ниската и накрая, за определяне на разликата на тези стойности. В този случай константата C не може да бъде записана. защото тя изчезва при извършване на изваждане. Разглеждаме някои интеграли с подробно решение. Намерете площта на обекта под една вълна. Сега ще разгледаме интеграли с подробно решение, което използва свойството на адитивност в първия пример и заместването на междинната интеграционна променлива във втория пример. Изчисляваме определен интеграл на една дробно рационална функция: y = (1 + t) / t 3 от t = 1 до t = 2. Сега ще покажем как да опростим вземането на интеграла чрез въвеждане на междинна променлива. Да предположим, че трябва да изчислим интеграла от (x + 1) 2 . Говорихме за определен интеграл за краен интервал [a, b] на функция f (x) непрекъсната върху него. Но редица специфични проблеми водят до необходимостта от разширяване на понятието за интеграл в случая, когато границите (едната или и двете) са равни на безкрайност, или когато прекъсната функция. Например, когато се изчисляват площи под криви, асимптотично се приближава към осите на координатите. За да се разшири концепцията за интеграла в този случай, в допълнение към прехода до границата при изчисляване на Riemann сума на апроксимиращите правоъгълници, се изпълнява друго. При такова двойно преминаване до границата се получава неподходящ интеграл. Обратно, всички гореспоменати интеграли се наричат правилни. 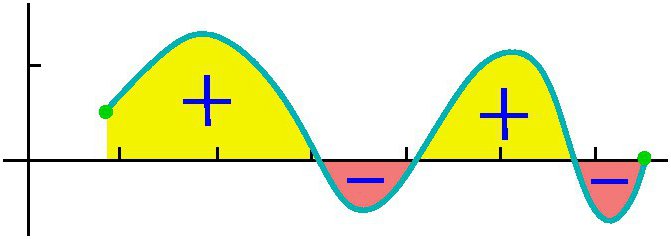 Така, за функцията, показана на фигурата по-горе, определеният интеграл от a до b ще бъде (S1 + S3) - (S2 + S4).
Така, за функцията, показана на фигурата по-горе, определеният интеграл от a до b ще бъде (S1 + S3) - (S2 + S4). Диференциал на определен интеграл
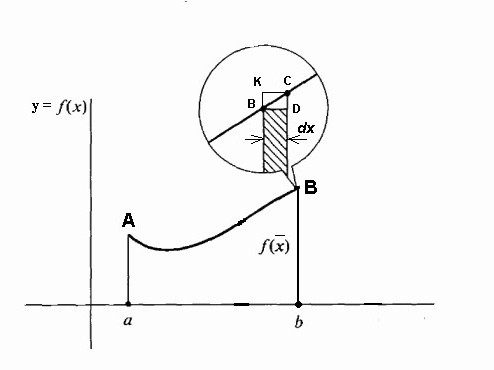 С фиксирана линия aA и движеща се Bb тази област става функция на f (x̃), като инкрементите Δx̃ все още се отлагат по оста x, а нарастването на функцията f (x̃) е нарастването на площта под кривата.
С фиксирана линия aA и движеща се Bb тази област става функция на f (x̃), като инкрементите Δx̃ все още се отлагат по оста x, а нарастването на функцията f (x̃) е нарастването на площта под кривата. 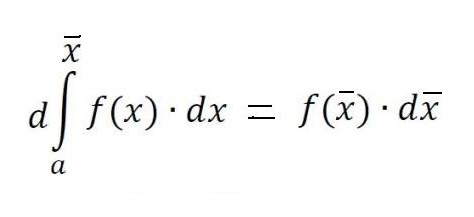
Основното съотношение на интегралното смятане
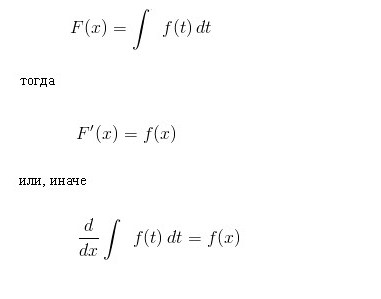
Основното правило за интеграция

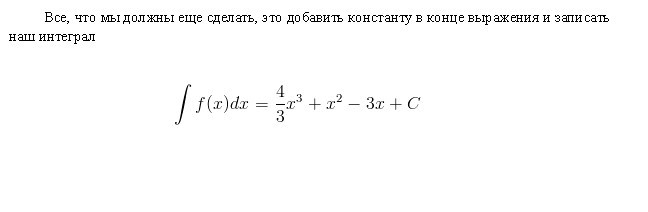

Интегрални таблици
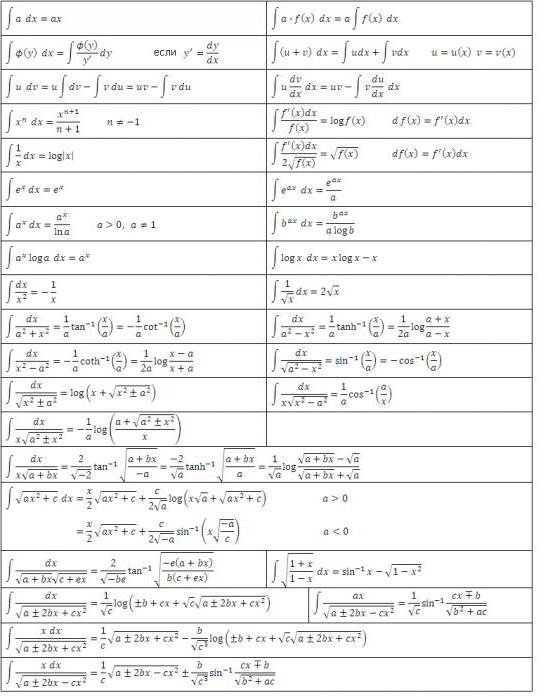

Как да се изчисли определен интеграл
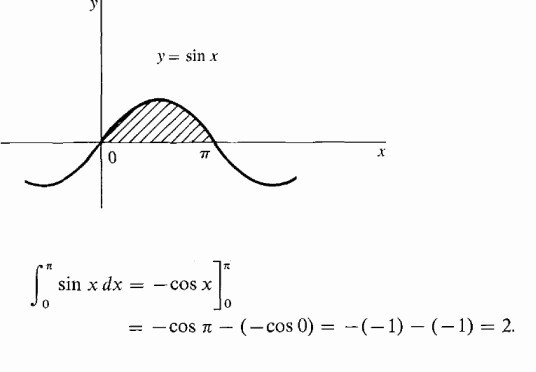 Изчислете защрихованата област под хиперболата.
Изчислете защрихованата област под хиперболата. 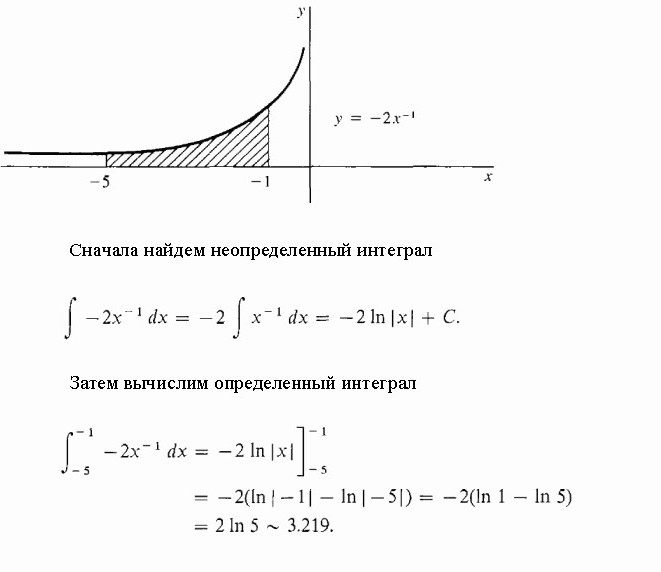
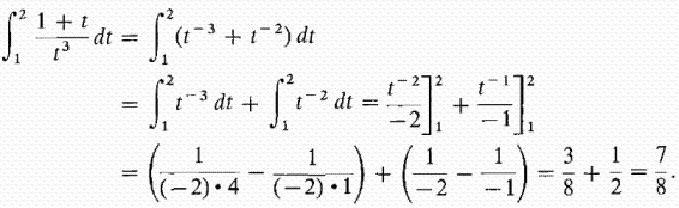
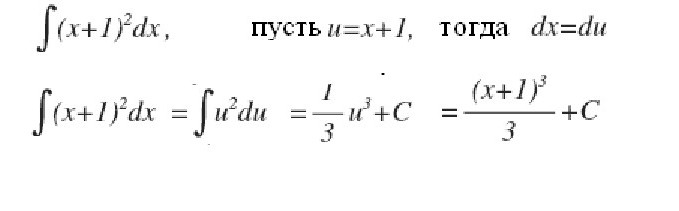
За неправилни интеграли