Какво е синус и косинус в тригонометрията?

Учителите вярват, че всеки ученик трябва да може да извършва изчисления, да знае тригонометрични формули, но не всеки учител обяснява какво са синус и косинус. Какво е тяхното значение, къде се използват? Защо говорим за триъгълници, а в учебника е очертан кръг? Нека се опитаме да обвържем всички факти.

Училищен предмет

Проучването на тригонометрията обикновено започва в 7-8 клас. По това време на учениците се казва какво са синус и косинус, те предлагат да решат геометрични проблеми, като използват тези функции. По-късно се появяват по-сложни формули и изрази, които се изискват да бъдат трансформирани по алгебричен начин (формули на двойни и половин ъгли, силови функции), а работата се извършва с тригонометричен кръг.

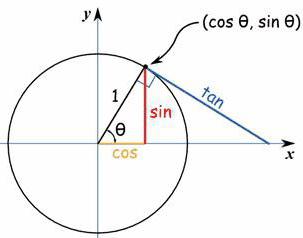Въпреки това учителите не винаги могат ясно да обяснят значението на използваните понятия и приложимостта на формулите. Затова ученикът често не вижда смисъл в тази тема и запаметената информация бързо се забравя. Все пак си струва да се обясни веднъж на ученик от гимназията, например връзката между функцията и колебателните движения и логическата връзка ще бъдат запомнени от много години, а шегите за безполезността на темата ще бъдат от миналото.

Използване на

Нека да погледнем заради любопитството в различни части на физиката. Искате ли да определите обхвата на снаряда? Или да изчислите силата на триене между обект и определена повърхност? Разклащането на махалото, гледането на лъчите, преминаващи през стъклото, изчислява индукцията? На практика във всяка формула се появяват тригонометрични понятия. И така, какво е синус и косинус?

дефинира

Синусът на ъгъла е съотношението на противоположния крак към хипотенузата, косинусът на съседния крак е същият за същата хипотенуза. Няма абсолютно нищо сложно. Може би учениците обикновено са объркани от стойностите, които виждат в тригонометричната таблица, защото се появяват квадратни корени. Да, излез от тях десетични дроби не е много удобно, но кой каза, че всички числа в математиката трябва да бъде дори?

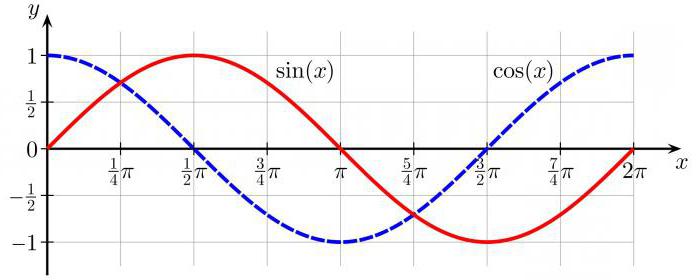Всъщност в проблемните книги на тригонометрията можете да намерите смешен намек: повечето от отговорите тук са дори и в най-лошия случай съдържат корена на две или три. Изводът е прост: ако в отговора получите „многоетажна“ фракция, проверете отново решението за грешки в изчисленията или в аргументите. И най-вероятно ще ги намерите.

Какво трябва да запомните

Както във всяка друга наука, в тригонометрията има такива данни, които трябва да бъдат научени.

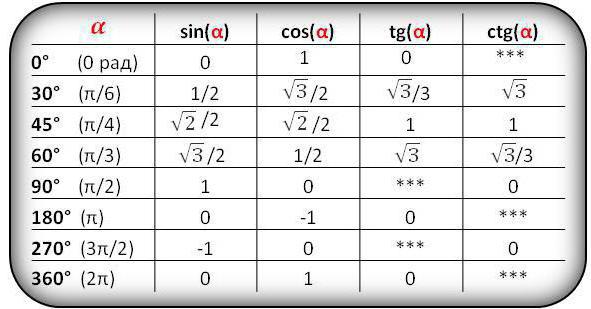
Първо, запомнете числените стойности за синусите, косинусите правоъгълен триъгълник 0 и 90, както и 30, 45 и 60 градуса. Тези показатели се намират в девет от десетте училищни задачи. Контролирайки тези стойности в учебника, ще изгубите много време и няма да има място за гледане на теста или изпита.

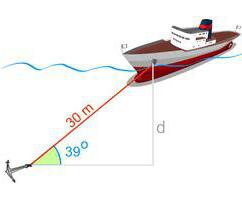Трябва да се помни, че стойността на двете функции не може да надвишава една. Ако някъде в изчисленията получите стойност извън диапазона 0-1, спрете и решете проблема отново.

Сумата от квадратите на синуса и косинуса е равна на единица. Ако вече сте намерили една от стойностите, използвайте тази формула, за да намерите останалите.

теорема

В основната тригонометрия има две основни теореми: синуси и косинуси.

Първият казва, че съотношението на всяка страна на триъгълника към синуса на противоположния ъгъл е същото. Вторият е, че квадратът на която и да е страна може да бъде получен чрез добавяне на квадратите на двете останали страни и изваждане на удвоения им продукт, умножен по косинуса на ъгъла между тях.

Така, ако сте в косинусова теорема Заменяйки стойността на ъгъла от 90 градуса, получаваме ... Питагоровата теорема. Сега, ако искате да изчислите площта на фигура, която не е правилен триъгълник, вече не можете да се притеснявате - двете разглеждани теореми значително ще опростят решението на проблема.

Цели и цели

Проучването на тригонометрията ще бъде значително опростено, когато осъзнаете един прост факт: всички действия, които изпълнявате, са насочени към постигане само на една цел. Всички параметри на триъгълник могат да бъдат намерени, ако знаете минималната информация за него - тя може да бъде стойността на един ъгъл и дължината на двете страни или, например, три страни.

За да се определи синус, косинус, тангенс на всеки ъгъл на тези данни е достатъчно, с тяхна помощ лесно можете да изчислите площта на фигурата. Почти винаги се изисква една от споменатите стойности като отговор и те могат да бъдат намерени по същите формули.

Несъответствия в изследването на тригонометрията

Едно от неясните въпроси, които студентите предпочитат да избягват, е да намерят връзката между различните понятия в тригонометрията. Изглежда, че триъгълниците се използват за изучаване на синусите и косинусите на ъглите, но по някаква причина символите често се намират на фигурата с кръг. Освен това има неразбираема вълнообразна графика, наречена синусоида, която няма външно сходство нито с кръг, нито с триъгълници.

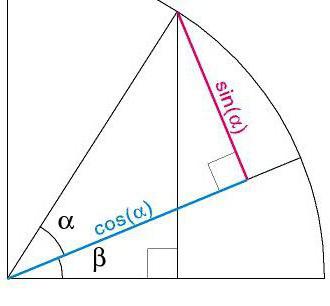Нещо повече, ъглите се измерват в градуси, след това в радиани, а числото Pi, написано просто като 3.14 (без единици), по някаква причина се появява във формулите, съответстващи на 180 градуса. Как всичко това е свързано един с друг?

Мерни единици

Защо пи точно 3.14? Помниш ли каква е тази стойност? Това е броят на радиусите, които се вписват в дъга на полукръг. Ако диаметърът на кръга е 2 сантиметра, обиколка ще бъде 3.14 * 2 или 6.28.

Втората точка: може би сте забелязали сходството на думите "радиан" и "радиус". Факт е, че един радиан е числено равен на ъгъла между центъра на окръжността и дъгата с дължина от един радиус.

Сега да комбинираме получените знания и да разберем защо думата „Pi на половина“ е написана на оста на координатите в тригонометрията, а отляво - „Pi“. Това е ъглова стойност, измерена в радиани, защото полукръгът е 180 градуса или 3,14 радиана. А там, където има степени, има синуси и косинуси. Триъгълникът лесно се държи от желаната точка, поставяйки сегментите в центъра и по оста на координатите.

Погледни в бъдещето

Тригонометрията, изучавана в училище, се занимава с праволинейна координатна система, където, колкото и странно да звучи, права линия е права линия.

Но има и по-сложни начини за работа с пространството: сумата на ъглите на триъгълника тук ще бъде повече от 180 градуса, а линията в нашия поглед ще изглежда като истинска дъга.

Да преминем от думи към дела! Вземете ябълка. Направете три разреза с нож, така че когато се гледа отгоре, получавате триъгълник. Извадете получената парче ябълка и погледнете "ребрата", където краят завършва. Те изобщо не са директни. Плодът в ръцете ви може да се нарече кръг, а сега си представете колко сложни трябва да бъдат формулите, с които можете да намерите областта на нарязаното парче. Но някои експерти решават подобни проблеми ежедневно.

Тригонометрични функции в живота

Забелязали ли сте, че най-краткият път на самолета от точка А до точка Б на повърхността на нашата планета има изразена форма на дъга? Причината е проста: земята е във формата на сфера, което означава, че не можете да изчислите много с помощта на триъгълници - тук трябва да използвате по-сложни формули

Не правете без синус / косинус на остър ъгъл във всички въпроси, свързани с пространството. Интересно е, че тук се срещат множество фактори: тригонометричните функции се изискват при изчисляване на движението на планетите в кръгове, елипси и различни траектории на по-сложни форми; процесът на изстрелване на ракети, спътници, совалки, откачване на изследователски апарати; наблюдение на далечни звезди и изучаване на галактики, които човек не може да постигне в обозримо бъдеще.

Като цяло полето за човешка дейност, което притежава тригонометрия, е много широко и очевидно само с течение на времето ще се разширява.

заключение

Днес сме се научили или, във всеки случай, повторихме какво са синус и косинус. Това са понятия, които не трябва да се страхуват - трябва да искате, и ще разберете тяхното значение. Не забравяйте, че тригонометрията не е цел, а само инструмент, който може да се използва за задоволяване на реални човешки нужди: изграждане на къщи, осигуряване на безопасност на движението, дори изследване на откритите пространства на Вселената.

Всъщност самата наука може да изглежда скучна, но след като веднъж откриете в него начин да постигнете собствените си цели, себереализация, процесът на обучение ще стане интересен и вашата лична мотивация ще се увеличи.

Като домашна работа, опитайте се да намерите начини за прилагане на тригонометрични функции в областта на дейност, която ви интересува лично. Представете си, включете въображението и тогава със сигурност ще откриете, че новите знания ще ви бъдат полезни в бъдеще. Освен това, математиката е полезна за общото развитие на мисленето.