Обемът на конуса, неговото изчисление

Геометрията като наука се формира в древен Египет и достига високо ниво на развитие. Известният философ Платон основава Академията, където се обръща голямо внимание на систематизирането на съществуващите знания. Конусът като един от геометрични фигури за първи път се споменава в известния трактат на Евклид "Началото". Евклид беше запознат с творбите на Платон. Сега малко хора знаят, че думата "конус" в превод от гръцки означава "шишарка". Гръцкият математик Евклид, който живее в Александрия, с право се счита за основател на геометричната алгебра. Древните гърци не само станали наследници на знанията на египтяните, но и значително разширили теорията.

История за определяне на конус

Геометрията като наука възниква от практическите изисквания за изграждане и наблюдение на природата. Постепенно експерименталното познание се обобщава и свойствата на някои тела се доказват чрез други. Древните гърци въвели понятието за аксиоми и доказателства. Axiom е твърдение, получено по практичен начин и не изискващо доказателство.

В книгата си Евклид цитира дефиницията на конус като фигура, която се получава чрез завъртане на правоъгълен триъгълник около един от краката. Той притежава и основната теорема, която определя обема на конуса. И тази теорема е доказана от древния гръцки математик Евдокс от Cnidus.

Друг математик от Древна Гърция, Аполоний Пергски, който е ученик на Евклид, разработва и излага теорията на коничните повърхности в своите книги. Той принадлежи към дефиницията на конична повърхност и сеанс към нея. Учениците от нашето време изучават евклидова геометрия, която е запазила основните теореми и дефиниции от древни времена.

Основни определения

Прав кръгъл конус се формира чрез завъртане на прав триъгълник около един крак. Както може да се види, понятието за конус не се е променило от дните на Евклид.

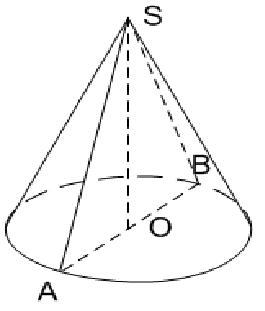
Hypotenusa AS правоъгълен триъгълник AOS, когато се върти около крака на операционната система, образува страничната повърхност на конуса, поради което се нарича генерична. Кракът на ОС на триъгълника се превръща едновременно във височината на конуса и неговата ос. Точка S става върхът на конуса. Catet AO, описващ кръга (основа), се превръща в радиус на конуса.

Ако равнината се изтегля от върха през върха и оста на конуса, тогава можете да видите, че получената аксиална част е равнобедрен триъгълник, в който оста е височината на триъгълника.

Също така често е необходимо да се изчисли страничната повърхност на тялото на оборота. Площта на страничната повърхност на конуса е равна на произведението от половината от дължината на обиколката на основата и образуващата конус.

S = C * L / 2 = n * R * L / 2

където С е обиколката на основата, l е дължината на образуващата конус, R е основният радиус.

Формулата за изчисляване на обема на конуса

Следната формула се използва за изчисляване на обема на конуса:

V = S * H ​​/ 3,

където S е площта на основата на конуса. Тъй като основата е кръг, нейната площ се изчислява, както следва:

S = nR ² .

От това следва:

V = n * R ² * H / 3,

където V е обемът на конуса;

n е число, равно на 3.14;

R е основният радиус, съответстващ на сегмент АО от Фигура 1;

H - височина, равна на сегмента OS.

Обем на пресечения конус

Има прав кръгъл конус. Ако равнината перпендикулярна на височината, отсече горната част, получавате пресечен конус. Двете му бази са с кръгла форма с радиуси R ₁ и R ₂ .

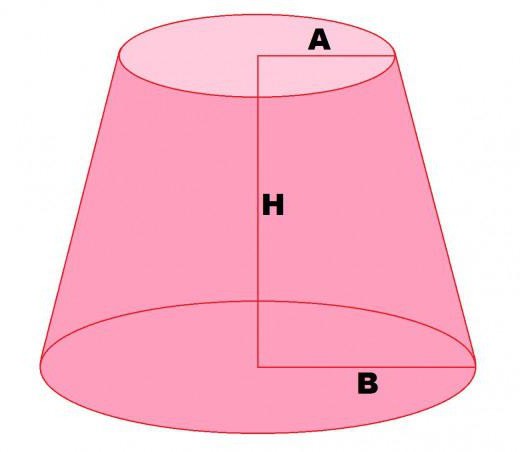
R1 = A;

R2 = В;

Н = Н.

Ако се образува прав конус чрез завъртане на прав триъгълник, тогава пресеченият конус се върти. правоъгълен трапец около правината страна.

Обемът на пресечения конус се изчислява по следната формула:

V = n * (R ' ² + R ₂ ² + R ₁ * R2) * Н / 3.

Конус и неговия участък със самолет

Древногръцкият перуански математик Аполоний Пергски принадлежи към теоретичната работа "Конична секция". Благодарение на неговата работа в геометрията се появяват определения на кривите: параболи, елипси, хиперболи. Помислете и тук е конус.

Вземете прав кръгъл конус. Ако равнината се пресича перпендикулярно на оста, в участъка се оформя кръг. Когато секантът пресече конуса под ъгъл спрямо оста, в секцията се получава елипса.

Секантната равнина, перпендикулярна на основата и успоредна на оста на конуса, образува хипербола на повърхността. Равнина, която срязва конуса под ъгъл спрямо основата и е успоредна на допирателната към конуса, създава крива на повърхността, която се нарича парабола.

Решаване на проблеми

Дори простата задача как да се направи кофа с определен обем изисква познание. Например, трябва да изчислите размера на кофата, така че да има обем от 10 литра.

дадено:

V = 10 1 = 10 dm ³ ;

R1 = 15 cm;

R ₂ = 25 cm.

Обхватът на конуса има формата, показана на фигура 3.

L - образуване на конус.

За да намерите площта на кофата, която се изчислява по следната формула:

S = n * (R ₁ + R ₂ ) * L,

необходимо е да се изчисли генератора. Намираме го от обема V = n * (R ₁ ² + R ₂ ² + R ₁ * R ₂ ) * H / 3.

Следователно, Н = 3V / n * (R'2 + R ₂ ² + R ₁ * R2).

Пресечен конус се оформя чрез въртене на правоъгълна трапеция, в която страничната страна образува конус.

L2 = (R2R1) ² + Н2.

Сега имаме всички данни за изграждане на кърпа за рисуване.

Защо огнените кофи са оформени като конус?

Кой си мислеше защо пожарните кофи имат привидно странна конична форма? И това не е просто. Оказва се, че конична кофа за гасене на пожар има много предимства пред конвенционалната форма на пресечен конус.

Първо, както се оказва, пожарната кофа се пълни с вода по-бързо и не се разлива, когато се носи. Конус, който е по-голям от обикновената кофа в даден момент, позволява прехвърлянето на повече вода.

Второ, водата от нея може да бъде изхвърлена на по-голямо разстояние, отколкото от обикновена кофа.

Трето, ако коничната кофа се освободи от ръцете и попадне в огъня, цялата вода се излива върху източника на огъня.

Всички тези фактори могат да спестят време - основният фактор при гасене на пожар.

Практическо приложение

Учениците често имат въпрос защо трябва да се научат как да изчисляват обема на различните геометрични тела, включително конуса.

И дизайнерите постоянно са изправени пред необходимостта да изчислят обема на коничните части на частите на механизмите. Това са върхове на свредла, части на стругови и фрезови машини. Формата на конуса ще позволи на свредлата лесно да влязат в материала, без да се изисква първоначално окачване със специален инструмент.

Обемът на конуса има купчина пясък или пръст, изсипани на земята. Ако е необходимо, като направите прости измервания, можете да изчислите неговия обем. Някои ще бъдат объркани от въпроса как да се намери радиусът и височината на купчината пясък. Въоръжен с лента мярка, измерване на обиколката на хълм C. По формулата R = C / 2n, ние научаваме радиуса. Хвърляйки върха (лента), откриваме дължината на генератора. И изчисли височината на Питагоровата теорема и обемът не е труден. Разбира се, такова изчисление е приблизително, но ви позволява да определите дали не сте излъгали, като донесете тон пясък вместо куб.

Някои сгради имат формата на пресечен конус. Например, телевизионната кула на Останкино се приближава към конусовидна форма. Тя може да бъде представена като състояща се от два конуса, поставени една върху друга. Куполите на древни замъци и катедрали са конус, обемът на който древните архитекти изчисляват с невероятна точност.

Ако се вгледате внимателно в околните предмети, много от тях са конуси:

• Консервни кутии за поливане на течности;
• високоговорител за клаксон;
• Конуси за паркиране;
• абажур за подовата лампа;
• позната коледна елха;
• духови инструменти.

Както може да се види от горните примери, възможността за изчисляване на обема на конуса, площта на нейната повърхност е необходима в професионалния и ежедневния живот. Надяваме се, че статията ще ви помогне.