Периметърът на квадрат и правоъгълник. Методи за определяне и примери за решения.

Често в интернет можете да откриете подигравки за това как познанията по математика - интеграли, диференциали, тригонометрични функции и други раздели на темата - не помагат за облекчаване на живота на човека. Такива вицове са напразни, тъй като помага за правилното изчисляване на периметъра на квадрат, правоъгълник и други геометрични форми в строителните работи. Консумация на материали: плочки, тапети, подови настилки - не може да се определи без разбиране на елементарни математически формули и геометрични форми.

Квадратни свойства

Всички изчисления в математиката се основават на свойствата на обекта. За да отговорим на въпроса: „Какъв е периметърът на квадрата?” - препоръчително е да си припомним отличителните характеристики на тази фигура.

1. Равенство на всички страни.
2. Наличието на четири ъгъла от 90 градуса.
3. Паралелизъм на страните.
4. Осева симетрия. Когато фигурата се върти, външният му вид остава непроменен.
5. Способност за описване и влизане в кръга.
6. Диагоналите в пресечката се разделят на половина.
7. Областта на фигурата характеризира пространството, изпълнено с квадрат в двуизмерно пространство.
8. Периметърът на фигурата не е нищо друго освен сумата от дължините на неговите страни.
9. От предишното свойство следва, че мерните единици по периметъра ще бъдат единици дължина: m, cm, dm и други.

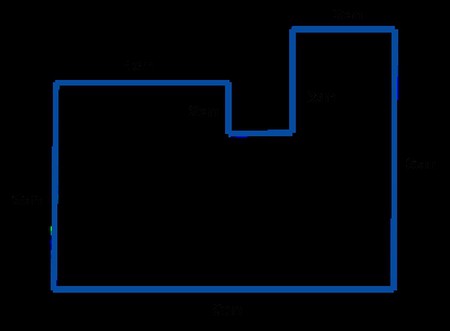
За да преброите плочите за завършване на ремонти в квадратна стая, трябва да знаете дължината на стаята. За да направите това, изчислете нейния периметър.

периметър

Преведено от гръцката дума означава "мярка наоколо." Терминът се отнася за всички затворени форми: квадрат, кръг, правоъгълник, триъгълник, трапец и други. Познаването на периметъра на елементарни фигури е необходимо за решаване на сложни геометрични проблеми с обекти с неправилна форма. Например, за да изчислите цокъла в помещение с оформление от тип “G”, или както се нарича “boot”, ще е необходимо да определите периметъра на квадрат и правоъгълник. В крайна сметка формата на стаята се състои от тези елементарни фигури.

Стандартното обозначение на такъв размер е буквата R. Всяка цифра, като се имат предвид нейните свойства, има своя собствена формула за определяне на периметъра.

Свойства с правоъгълник

1. Равенство на противоположните страни.
2. Равенство на диагоналите.
3. Способност за описване на кръга.
4. Височините на правоъгълника са равни на страните.
5. Сумата на ъглите е 360 градуса и всички ъгли са прави.
6. Паралелизъм на противоположните страни.
7. Перпендикулярност на съседните страни.
8. Сумата от квадратите на диагоналите на правоъгълника е равна на сумата от квадратите на неговите страни.
9. Пресичащи се, диагоналите се разделят на половина.
10. Неспособност за поставяне на кръг във форма.

Площ на периметъра

В зависимост от установените (известни) параметри на квадрата съществуват различни формули за определяне на неговия периметър. Проста задача е да се изчисли периметърът на фиксирана дължина на неговата страна (и). В този случай Р = с + с + с + с или 4 * с. Например, дължината на страната на квадрата е 7 см, след което периметърът на фигурата ще бъде 28 см (4 * 7).

В първия случай всичко е ясно, но как да намерите периметъра квадрат, знаейки неговия район? И тук всичко е много ясно. Тъй като площта на фигурата се определя чрез умножаване на едната страна с другата и всички страни са равни на квадрата, е необходимо да се извлече коренът от известна стойност. Пример: има квадрат с площ от 25 dm ² . Коренът на 25 е 5 - тази стойност характеризира дължината на страната на квадрата. Сега, замествайки намерената стойност - 5 dm ² - в оригиналната периметрова формула, можем да решим проблема. Отговорът ще бъде 20 dm. Това означава, че 4, умножено по 5, получи желаната стойност.

Квадрат и кръг

От свойствата на разглежданата фигура изглежда, че кръг може да бъде вписан в квадрат и също да бъде описан около фигурата.

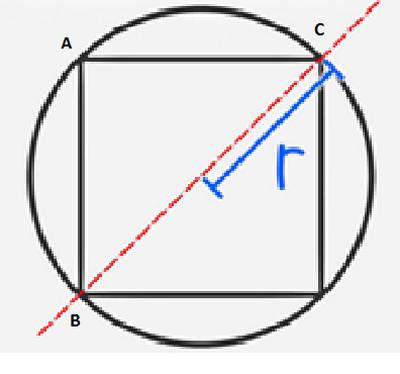
Първият вариант е да се намери периметъра по обиколката на кръга. Вписаният е квадрат, чиито върхове са в кръг. Радиусът на кръга е 1/2 диагонална дължина. Оказва се, че диаметърът е равен на диагонала. Сега трябва да помислите правоъгълен триъгълник което е резултат от разделянето на диагонала на площада. Решаването на проблема се свежда до намиране на страните на този триъгълник. BC е известна стойност, диаметърът на кръга. Да предположим, че е равен на 3 см. Питагоровата теорема в случая на равните страни на триъгълника ще изглежда така: 2с ² = 3 ² . Във формулата символът s е дължината на страната на триъгълника и квадрата; 3 - известната стойност на хипотенузата. Следователно, c = /9 / 2. Знаейки страната на площада, неговият периметър не е проблем да се изчисли.

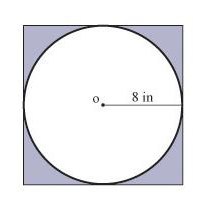
Характеристика на вписания кръг е разделянето на страните на квадрата на половина. Следователно радиусът е равен на половината от дължината на страната на квадрата. След това c = 2 * радиус. Периметърът на квадрата в този случай е 4 * 2 * радиус или 8 радиуса на окръжност.

Правоъгълник в периметъра

Най-елементарната формула за определяне на периметъра на правоъгълника чрез известните стойности на неговите страни е следната: P = 2 (a + b), където a и b са дължините на страните на фигурата.

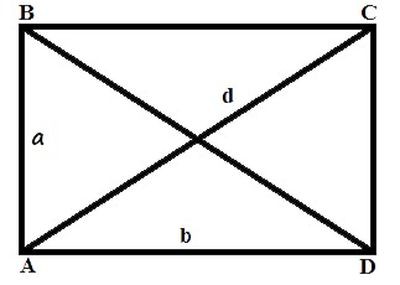
Диагоналът на правоъгълник, подобен на квадрат, разделя фигурата наполовина, образувайки правоъгълен триъгълник. Но задачата се усложнява от факта, че страните на този триъгълник са неравномерни. В случай на известна стойност на една от страните и диагонал, втората може да се намери, като се следва теоремата на Питагор: d ² = a ² + в ² , където а и v са страни на фигурата, а d е диагоналът.

Ако нито една от страните не е неизвестна, знанието за тригонометрията влиза в сила: sines, cosines и други функции.

Намирането на периметъра по описаната окръжност и известният диаметър се свежда до факта, че диаметърът е равен на дължината на диагонала на фигурата. Освен това, решението на проблема се определя от наличието на известни количества. Ако са дадени ъгли, а след това чрез тригонометрични функции. Ако е дадена страна, отговорът ще бъде намерен чрез Питагоровата теорема.

Правоъгълник и тригонометрични функции

За яснота е пример за решаване на проблема. Дадено: правоъгълник AVSD; диагонална дължина ( d ) 20 cm; ъгъл f - 30 °. Намерете периметъра на фигурата.

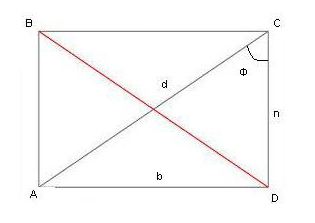
От тригонометрията е необходимо да се припомни следното: синусът на ъгъл в правоъгълен триъгълник е равен на съотношението на противоположния крак към хипотенузата. Синусът от 30 ° (има таблици, по които може да се определят стойностите на тригонометричните функции за правилните ъгли) е 1/2. Оказва се 1/2 = съотношение в d . Неизвестната стойност в ще бъде равна на d / 2 = 20/2 = 10 cm.

За да изчислите периметъра, трябва да намерите втората страна на фигурата. Възможно е чрез теоремата на Питагорей, тъй като дължините на хипотенузата и един от краката са известни, или отново чрез аспектното съотношение за косинуса на ъгъла.

Косинусът на ъгъла as се изразява като съотношение на съседния крак към хипотенузата и е равно на /3 / 2.

/3 / 2 = n / d , n = (d * )3) / 2 или 10 * .3. След извличане на корена от 3, получаваме дължината на страната на триъгълника: 10 * 1.73 = 17.3 cm.

Периметърът е 2 (17.3 + 10) = 2 * 27.3 = 54.6 cm.

Периметър и отношение

В училищната програма съществуват проблеми в геометрията, когато дължините на страните на правоъгълника се изразяват в отношението им един към друг. Разглеждането на решението на този проблем е представено по-долу.

Известно е, че сумата от дължините на всички страни на правоъгълник, т.е. нейният периметър, е 84 см. Съотношението на дължината (d) към ширината (w) е 3: 2. Намерете страните на фигурата.

Решение: Нека дължината е 3x, а ширината 2x, в зависимост от отношението от състоянието на проблема. Формулата на периметъра на правоъгълника с данни за дължините на страните ще бъде както следва: 3x + 3x + 2x + 2x = 84. Освен това, 10x = 84, x = 8.4 см. Като замениш x в израза на дължината и ширината на правоъгълника, може да намериш желаните стойности. Дължината ще бъде: 3 * 8.4 = 25.2 cm; ширина: 2 * 8.4 = 16.8 cm.

Статията е посветена на решаването на най-често срещаните задачи в учебната програма. И това не са всички начини за намиране на периметъра на квадрат и правоъгълник.