Знаци, съставни елементи и свойства на равнобедрен триъгълник

Първите историци на нашата цивилизация - древните гърци - споменават Египет като родно място на геометрията. Трудно е да не се съглася с тях, знаейки с каква огромна прецизност са издигнати гигантските гробници на фараоните. Взаимното подреждане на пирамидалните равнини, техните пропорции, ориентация по кардиналните точки - би било немислимо да се постигне такова съвършенство, без да се познават основите на геометрията.

Думата "геометрия" може да бъде преведена като "измерение на земята". А думата "земя" се появява не като планета - част от Слънчевата система, а като равнина. Маркирането на площите за земеделие, най-вероятно, е първоначалната основа на науката за геометричните форми, техните видове и свойства.

Триъгълникът е най-простата пространствена фигура на планиметрия, съдържаща само три точки - върхове (не може да има по-малко). В основата на основите може да бъде причината за нещо загадъчно и древно. Всевиждащото око вътре в триъгълника е едно от най-ранните познати окултни знаци, а географията на нейното разпространение и времевата рамка са просто невероятни. От древните египетски, шумерски, ацтекски и други цивилизации до по-модерни общности на окултни любители, разпръснати по целия свят.

Какви са триъгълниците

Редовният многостранен триъгълник е затворена геометрична фигура, състояща се от три сегмента с различна дължина и три ъгъла, нито една от които не е правилна. Освен това има няколко специални вида.

Острият триъгълник има всички ъгли под 90 градуса. С други думи - всички ъгли на такъв триъгълник са остри.

Прав триъгълник над които учениците плачеха през цялото време поради изобилието от теореми, има един ъгъл с магнитуд 90 градуса или, както се нарича, права линия.

Тъпичният триъгълник се отличава с факта, че един от нейните ъгли е тъп, т.е. неговата величина е повече от 90 градуса.

Равностранен триъгълник има три страни със същата дължина. Такава фигура също има всички ъгли.

Накрая, в равнобедрен триъгълник от три страни, двете са равни.

Отличителни черти

Свойствата на равнобедрен триъгълник също определят неговата основна, основна разлика - равенството на двете страни. Тези страни, които са еднакви, се наричат ​​бедра (или по-често странични страни), но третата страна се нарича "основа".

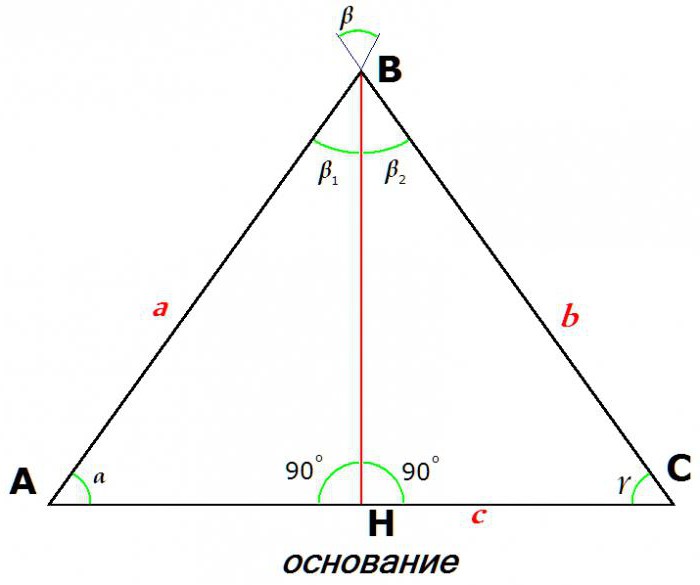
На тази фигура a = b.

Вторият знак на равнобедрен триъгълник следва от синусната теорема. Тъй като страните а и b са равни, синусите на техните противоположни ъгли са равни:

a / sin γ = b / sin α, откъдето имаме: sin γ = sin α.

Равенството на синусите предполага равенство на ъгли: γ = α.

Така че, вторият знак на равнобедрен триъгълник е равенството на два ъгъла, съседни на основата.

Третият знак. Триъгълникът разграничава такива елементи като височина, симетрия и медиана.

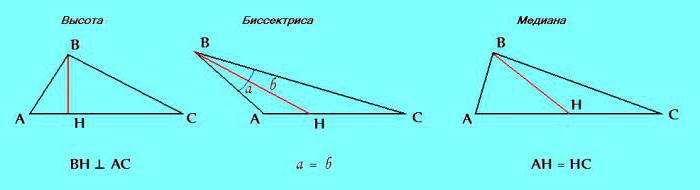
Ако в процеса на решаване на проблема се окаже, че в разглеждания триъгълник два от тези елементи са еднакви: височина с ъглополовяща; ъглополовяща с медиана; медиана с височина - определено е възможно да се заключи, че триъгълникът е равнобедрен.

Геометрични свойства на фигурата

1. Свойства на равнобедрен триъгълник. Едно от отличителните качества на фигурата е равенството на ъглите, съседни на основата:

α = γ;

<YOU = <BCA.

2. Друг обект, разгледан по-горе: медианата, симетрията и височината в равнобедрен триъгълник съвпадат, ако са изградени от неговия връх до основата.

3. Равенство на бисектрисите, изтеглени от върховете в основата:

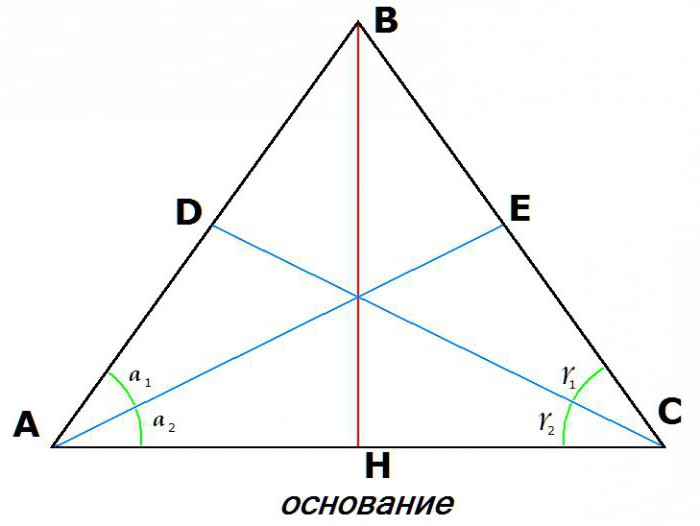
Ако AE е bisector на ъгъла YOU, и CD е bisector на ъгъла BCA, а след това: AE = DC.

4. Свойствата на равнобедрен триъгълник също осигуряват равенството на височините, които се извличат от върховете в основата.

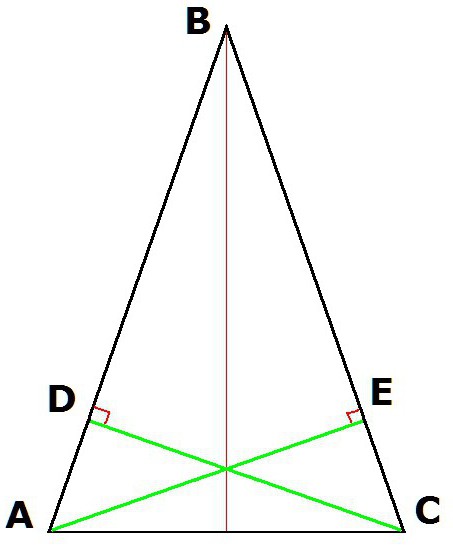
Ако построим височините на триъгълника ABC (където AB = BC) от върховете A и C, тогава получените сегменти CD и AE ще бъдат равни.

5. Медианите, изтеглени от ъглите в основата, също ще бъдат равни.

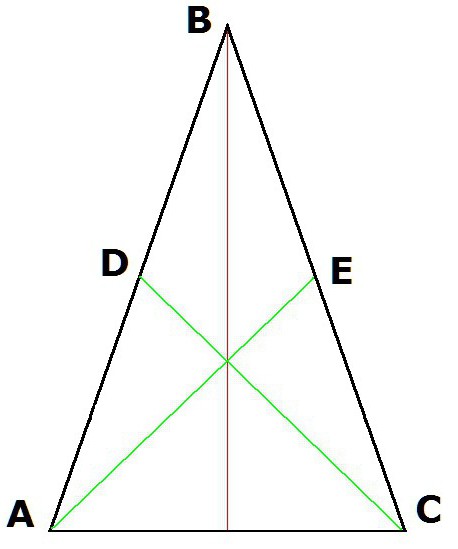
Така че, ако AE и DC са медиани, т.е. AD = DB, и BE = EC, тогава AE = DC.

Височина на равнобедрен триъгълник

Равенството на страните и ъглите при тях добавя някои особености при изчисляването на дължините на елементите на разглежданата фигура.

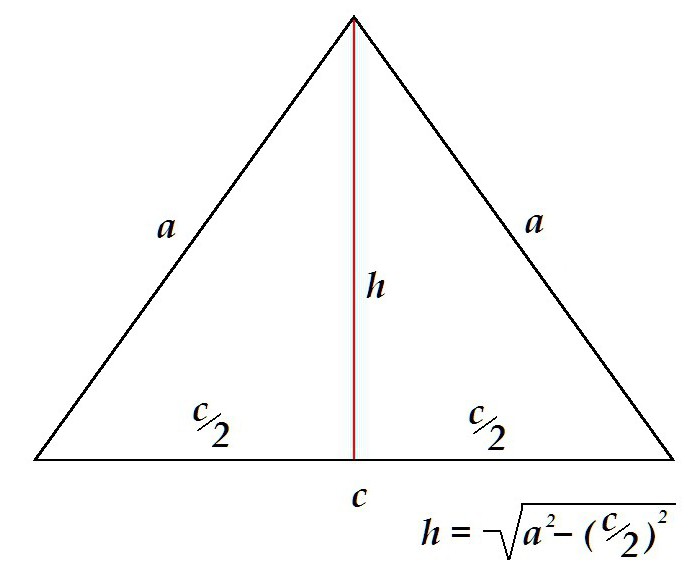
Височината в равнобедрен триъгълник разделя фигурата на 2 симетрични правоъгълни триъгълника с хипотенузи, в които се проектират страни. Височината в този случай се определя от Питагоровата теорема като крак.

Един триъгълник може да бъде равен на всичките три страни, след това ще бъде наречен равностранен. Височината в равностранен триъгълник се определя по същия начин, само за изчисления е достатъчно да се знае само една стойност - дължината на страната на този триъгълник.

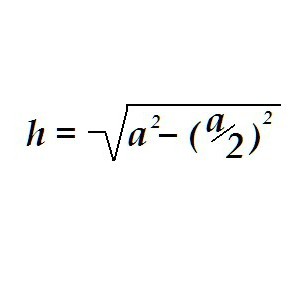
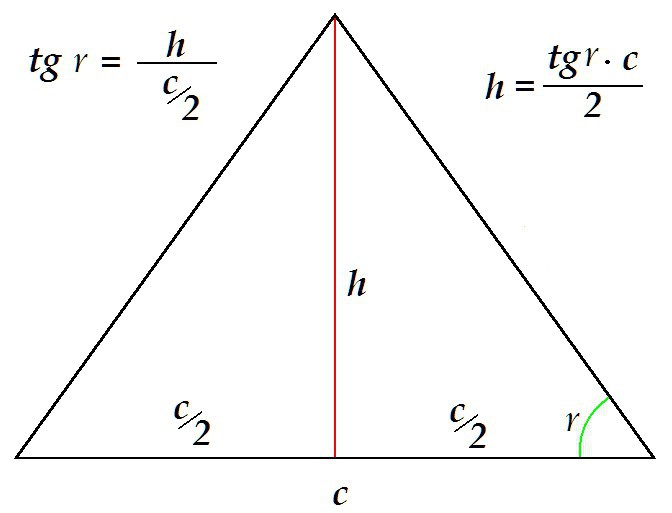
Възможно е да се определи височината по друг начин, например, като се знае основата и ъгълът, който е съседен на него.

Медиана на равнобедрен триъгълник

Разглежданият тип триъгълник, поради неговите геометрични характеристики, се решава съвсем просто чрез минималния набор от изходни данни. Тъй като медианата в равнобедрен триъгълник е равна както на неговата височина, така и на бисектриса, алгоритъмът за неговото определяне не се различава от реда, в който са изчислени тези елементи.

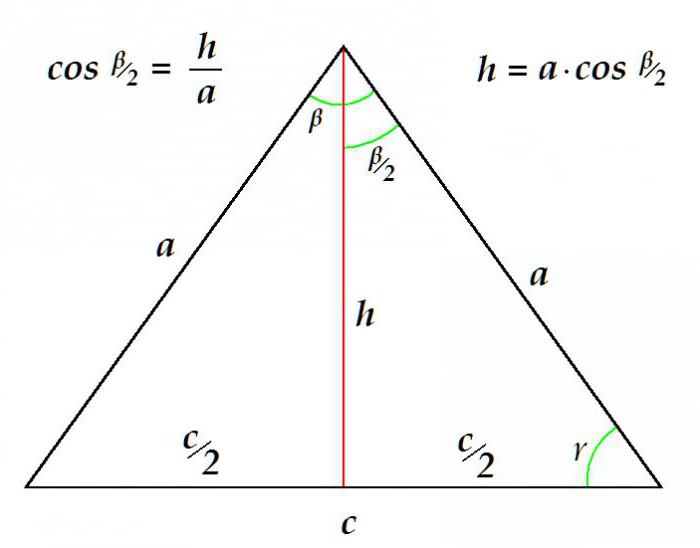
Например, можете да определите дължината на медианата от известната страна и ъгъла на върха.

Как да определим периметъра

Тъй като в разглежданата контурна фигура двете страни са винаги еднакви, тогава за определяне на периметъра е достатъчно да се знае дължината на основата и дължината на една от страните.

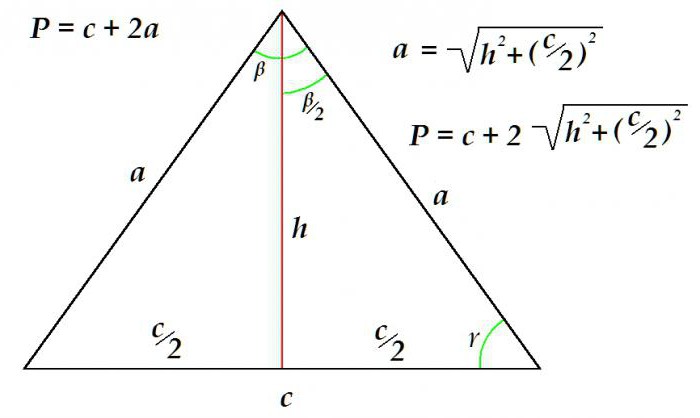
Помислете за пример кога да се определи периметър на триъгълник от известната основа и височина.

Периметърът е равен на сумата на основата и двойната дължина на страната. Страната, от своя страна, се определя с помощта на Питагоровата теорема като хипотенуза на правоъгълен триъгълник. Дължината му е равна на квадратен корен от сумата на квадрата на височината и квадрата на половината база.

Площ на равнобедрен триъгълник

По правило съществуват трудности и изчисляване на площта на равнобедрен триъгълник. Универсалното правило за определяне на площта на триъгълника като половината от произведението на основата до неговата височина важи, разбира се, и в нашия случай. Но свойствата на равнобедрен триъгълник правят задачата по-лесна.

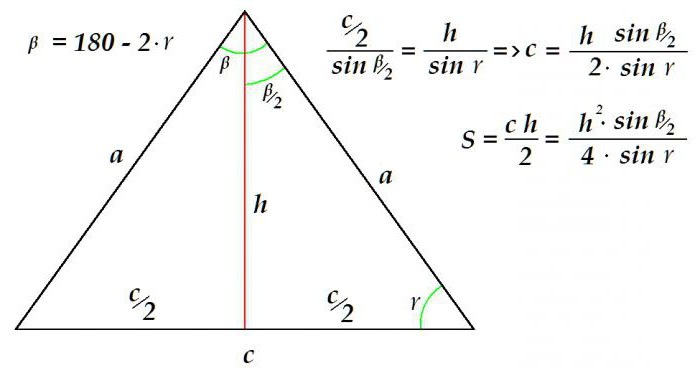
Да приемем, че височината и ъгълът в близост до основата са известни. Необходимо е да се определи площта на фигурата. Това може да се направи по този начин.

Тъй като сумата на ъглите на всеки триъгълник е 180 °, тогава е лесно да се определи ъгълът. Освен това, използвайки пропорцията, съставена според синус теоремата, се определя дължината на основата на триъгълника. Налични са всичко, базата и височината - достатъчно данни за определяне на площта.

Други свойства на равнобедрен триъгълник

Позицията на центъра на окръжност, описана около равнобедрен триъгълник, зависи от ъгъла на върха. Така че, ако равнобедрен триъгълник е остър, центърът на кръга се намира вътре във фигурата.

Центърът на кръга, който е описан около равнобедрен триъгълник с тъпи страни, лежи извън него. И накрая, ако ъгълът при върха е 90 °, центърът се намира точно в средата на основата, а диаметърът на кръга минава през самата основа.

За да се определи радиусът на окръжност, описана около равнобедрен триъгълник, е достатъчно да се раздели дължината на страната с двойния косинус на половината от ъгъла на върха.