Остроградски - теорема и формула на Гаус

MV Остроградски - руски математик и физик от времето на Руската империя, академик. Той направи огромен принос за развитието математически анализ теория на вероятностите, механика (част от физиката) теория на числата. През 1826 г. той извлича формула, която сега се нарича формула Остроградски-Гаус.

История на откриването

Формулата Остроградски-Гаус е спомената за първи път от Йозеф Лагранж през 1762 г.

Освен това основният метод за намаляване на тройния интеграл на повърхността е доказан от Карл Гаус, който използва решението на проблемите в електродинамиката като основа за доказателството. Това се случи през първата половина на XIX век.

Освен това формулата в общ вид беше представена от Михаил Остроградски. С негова помощ стана възможно да се изрази стойността на диференциала в параметър от N-пъти интеграл.

Значението на формулата Остроградски

Формулата Остроградски-Гаус свързва тройния интеграл върху пространствения обем с интеграла над повърхността на лицето му. Тя е аналог на формулата на Зелената, която свързва двоен интеграл върху равнина с криволинейно по протежение на неговите граници.

Извличане на формулата

Остроградски - формула Гаус: заключение. Да предположим, че в областта W е дефинирана функцията на интег- рендирането R (x, y, z), която е определена и непрекъсната. Неговото производно е сходно в цялата област W, включително неговата граница. В тази форма сега е известна теоремата Остроградски - Гаус (формулата е дадена по-долу).

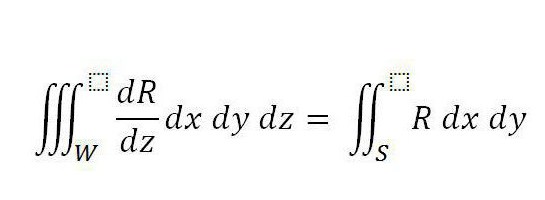
Нещо повече, S е повърхността, която свързва тялото, а интегралът отдясно е разпределен по външната му страна.

И абсолютно вярно

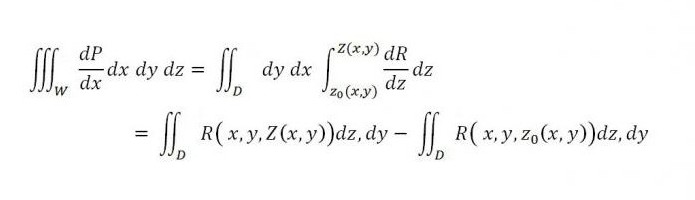
Ако по подобен начин вземем предвид интегралите по повърхността, тогава

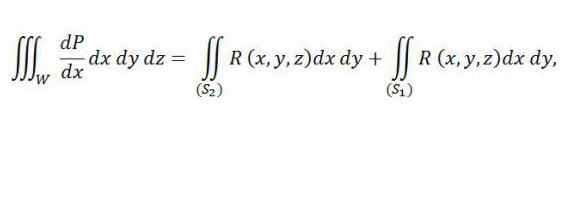
докато в дясно е сумата от два интеграла - първата е свързана с горната част на повърхността (S2), а втората - с долната част на повърхността (S1). Ако добавим към този равенство отдясно интеграла, посочен по-долу, неговата валидност няма да бъде нарушена:

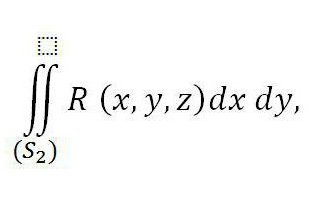
Тя съответства на външната част на повърхността S3 поради равенството до нула.

Ако комбинираме и трите горепосочени интеграла в един, ще получим специален случай на формулата Остроградски.

Лесно е да се разбере, че тази формула е вярна за по-широк клас тела и е валидна и за фигури, ограничени от абсолютно всякакви нелинейни повърхности.

По подобен начин важат следните формули:

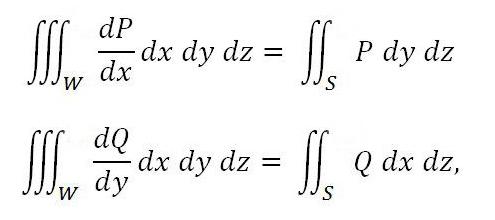
ако функциите Q и P са непрекъснати в областта заедно с техните производни dP / dx и dQ / dy.

Ако добавим и двете равенства, ще получим израза за формулата Остроградски. Той показва интеграла над повърхността, свързан с външната част на повърхността, чрез тройния интеграл, който се поема от самия орган, границата на която е горепосочената повърхност.

Трябва да се разбере, че формулите на Грийн, Стокс и Остроградски изразяват интеграла, свързан с определено геометрично тяло, чрез интеграл, който е взет на неговата граница. Формулата на Грийн се използва само в случай на двуизмерност на пространството, формулата на Стокс се прилага към изкривено двуизмерно пространство.

Формулата на Нютон-Лайбниц също може да се разглежда като някакъв аналог на тези формули, но за едномерно пространство.

Използването на тази формула

Нека непрекъснатите функции A, B и C се дават във всяка незатворена област на пространството, като се вземе всяка затворена повърхност, която е в даден регион и свързва определен орган, може да се разгледа следната интегрална над повърхността:

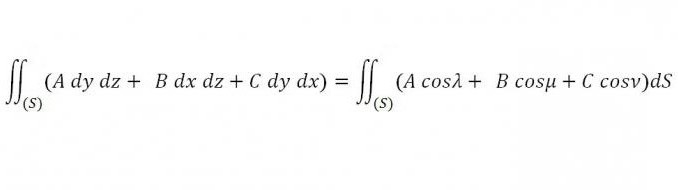
Необходимо е да се намерят такива стойности на A, B и C, така че за всеки x, y и z този интеграл да е равен на нула.

За целта използвайте формулата Остроградски-Гаус. Едно от подразбиращите се условия е сигурността и непрекъснатостта на функциите A, B и C и техните производни.

Необходимо е също да се въведе конкретно най-даденото ограничение за даден случай: както тялото, така и граничната повърхност трябва да се съдържат едновременно в определена и определена област, наречена просто свързана. Неговата основна характеристика е липсата на празно пространство (включително пространството на точките). Така границата на тялото ще бъде една и с тази единна повърхност.

След прилагане на формулата е възможно да се получи следното условие, което е достатъчно:

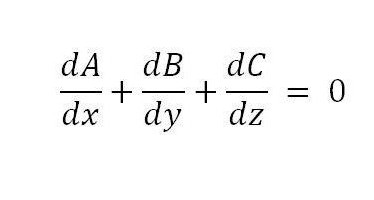
За да се докаже, че условието също е необходимо, достатъчно е да се използва диференциацията на тройния интеграл.

В заключение е необходимо да се каже за областите на използване.

Как се използва формулата Остроградски-Гаус на практика? Примери за използване могат да бъдат намерени в различни области: за извличане на някои формули във физиката (например уравнението на дифузията), трансформиране на интеграли, изчисляване на Gauss интеграли, доказване на някои формули и много други.