Как да намерим радиуса на кръг. Вписан и описан кръг

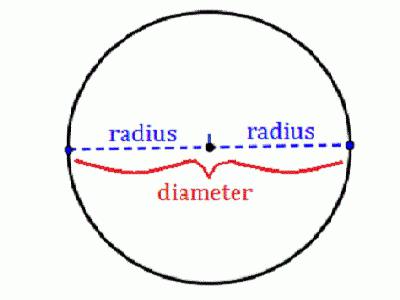
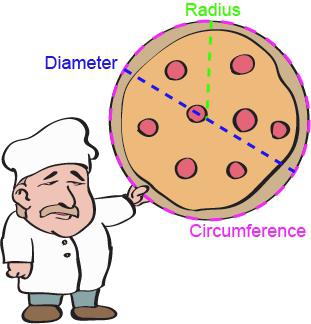
Радиусът е сегмент, който свързва всяка точка от кръга с неговия център. Това е една от най-важните характеристики на тази цифра, тъй като на базата на нея можете да изчислите всички други параметри. Ако знаете как да намерите радиуса на кръг, можете да изчислите неговия диаметър, дължина и площ. В случай, че тази цифра е вписана или описана около друга, тогава могат да бъдат решени няколко задачи. Днес ще разгледаме основните формули и особености на тяхното приложение.

Известни стойности

Ако знаете как да намерите радиуса на окръжност, която обикновено се обозначава с буквата R, тя може да се изчисли от една характеристика. Тези стойности включват:

• обиколка (C);
• диаметърът (D) е сегмент (или по-скоро хорда), който преминава през централната точка;
• площ (S) - пространство, което е ограничено до тази цифра.

По обиколката

Ако стойността на С е известна в задачата, тогава R = C / (2 * P). Тази формула е дериват. Ако знаем какво е то дължина на окръжността тогава не е нужно да помните. Да предположим, че при задача C = 20 м. Как да намерим радиуса на окръжност в този случай? Просто заменете известната стойност в горната формула. Отбележете, че при такива проблеми винаги се подразбира знанието на числото P. За удобство на изчисленията, ние приемаме нейната стойност като 3.14. Решението в този случай е следното: запишете какви стойности са дадени, извлечете формулата и извършете изчисления. В отговора пишем, че радиусът е 20 / (2 * 3,14) = 3,19 м. Важно е да не се забравя какво си мислим и да се споменава името на мерните единици.

По диаметър

Веднага подчертаваме, че това е най-простият тип проблем, който пита как да се намери радиусът на окръжност. Ако получите такъв пример на контрола, тогава можете да бъдете спокойни. Тя дори не се нуждае от калкулатор! Както казахме, диаметърът е сегмент или, по-правилно, акорд, който минава през центъра. Нещо повече, всички точки на окръжността са равноотстоящи. Следователно, тази струна се състои от две половини. Всеки от тях е радиус, който следва от дефиницията му като сегмент, който свързва точка на кръга и неговия център. Ако диаметърът на проблема е известен, тогава за да намерите радиуса, просто трябва да разделите тази стойност на две. Формулата е следната: R = D / 2. Например, ако диаметърът в задачата е 10 m, тогава радиусът е 5 метра.

По площ от кръга

Този тип задачи обикновено се наричат ​​най-трудни. Това се дължи най-вече на липсата на познаване на формулата. Ако знаете как да намерите радиуса на кръг в този случай, тогава останалото е въпрос на техника. В калкулатора трябва само предварително да намерите иконата на квадратния корен. Площта на окръжността е произведението на числото P и радиуса, умножен по себе си. Формулата е следната: S = P * R ² . Разделяйки радиуса от едната страна на уравнението, лесно можете да разрешите проблема. Тя ще бъде равна на квадратен корен от частното на площта, разделена на числото P. Ако S = 10 m, тогава R = 1,78 метра. Както и при предишните задачи, важно е да не забравяме използваните единици.

Как да намерим радиуса на кръга

Да предположим, че a, b, c са страни на триъгълник. Ако знаете техните стойности, тогава можете да намерите радиуса на кръга, описан около него. За да направите това, първо трябва да намерите полу-периметър на триъгълника. За да ви улесним при четенето, нека го отбележим с малка буква p. Тя ще бъде равна на половината от сумата на страните. Формулата му е: p = (a + b + c) / 2.

Също така се изчислява произведението на дължините на страните. За удобство ще го обозначим с буквата S. Формулата за радиуса на описаната окръжност ще изглежда така: R = S / (4 * √ (p * (p - a) * (p - b) * (p - c)).

Помислете за примерна задача. Имаме окръжност, описана около триъгълник. Дължините на страните му са 5, 6 и 7 см. Първо се изчислява полу-периметърът. В нашия проблем тя ще бъде равна на 9 сантиметра. Сега изчисляваме произведението на дължините на страните - 210. Заместваме резултатите от междинните изчисления във формулата и откриваме резултата. Радиусът на описаната окръжност е 3,57 сантиметра. Записваме отговора, без да забравяме за мерните единици.

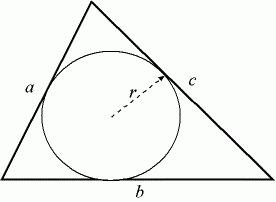
Как да намерим радиуса на вписания кръг

Да предположим, че a, b, c са дължините на страните на триъгълника. Ако знаете техните стойности, тогава можете да намерите радиуса на вписания в него кръг. Първо трябва да намерите неговия полу-периметър. За по-лесно разбиране ние го обозначаваме с малка буква p. Формулата за изчисляването му е, както следва: p = (a + b + c) / 2. Този тип задача е малко по-опростена от предишната, така че не са необходими повече междинни изчисления.

Радиусът на вписаната окръжност се изчислява по следната формула: R = √ ((p - a) * (p - b) * (p - c) / p). Помислете за това с конкретен пример. Да предположим, че проблемът описва триъгълник със страни от 5, 7 и 10 см. В него е вписан кръг, чийто радиус трябва да бъде намерен. Първо откриваме полупериметър. В нашия проблем той ще бъде равен на 11 см. Сега ще го заменим с основната формула. Радиусът ще бъде равен на 1,65 сантиметра. Записваме отговора и не забравяме за правилните единици.

Кръг и неговите свойства

всеки геометрична форма има свои характеристики. От тяхното разбиране е, че зависи правилността на решаването на проблемите. Те имат кръг. Често те се използват при решаването на примери с описани или вписани цифри, тъй като те дават ясна представа за тази ситуация. Сред тях са:

• Права линия може да има нула, една или две пресечни точки с кръг. В първия случай той не се пресича с него, а във втория е допирателна, а в третата - секутна.
• Ако вземем три точки, които не лежат на една права линия, тогава през тях може да се изтегли само един кръг.
• Права линия може да бъде допирателна от две фигури едновременно. В този случай тя ще премине през точката, която лежи на сегмента, свързващ центровете на кръговете. Дължината му е равна на сумата от радиусите на тези цифри.
• Чрез една или две точки можете да извлечете безкраен брой кръгове.