Фракция - какво е това? Видове фракции

Изучавайки кралицата на всички науки - математика, в определен момент всеки се сблъсква с фракции. Въпреки че тази концепция (като самите видове фракции или математически операции с тях) е доста проста, тя трябва да бъде третирана внимателно, защото в реалния живот извън училище тя ще бъде много полезна. Затова нека освежим знанията си за фракциите: какво е то, за какво е, какви са те и как да извършват различни аритметични операции с тях.

Фракцията на Нейно Величество: Какво е това?

Фракциите в математиката са числа, всяка от които се състои от една или повече части от единица. Такива фракции се наричат ​​също обикновени или прости фракции. Като правило, те са написани под формата на две числа, които са разделени от хоризонтална или наклонена черта, наричана е "частична". Например: ½, ¾.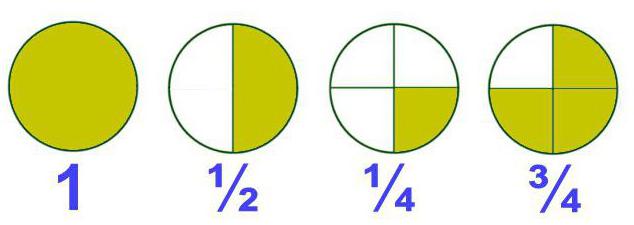

Горната, или първата от тези числа, е числителят (показва колко части са взети от числото), а долната, или втората, е знаменателят (показва колко единици са разделени на едно).

Фракционната лента действително изпълнява функцията на знак за деление. Например 7: 9 = 7/9

Традиционно обикновените фракции са по-малко от една. Докато десетичните числа могат да бъдат по-големи от нейните.

За какво са дроби? Да, за всичко, защото в реалния свят не всички числа са цели числа. Например две ученички в трапезарията купиха един вкусен шоколад в кесията. Когато се готвеха да споделят десерт, те срещнали приятелка и решили да я лекуват с нея. Въпреки това, сега е необходимо правилно да се разделят шоколад бар, ако считаме, че той се състои от 12 квадрата.

Първоначално момичетата искаха да разделят всичко по еднакъв начин, а след това всеки да получи четири парчета. Но след като се замислиха, те решили да третират приятелка си, а не 1/3, но 1/4 шоколад. И тъй като ученичките са малко изучавани фракции, те не са взели предвид, че при такава ситуация, в резултат на това, те ще имат 9 парчета, които са много зле разделени на две. Този сравнително прост пример показва колко е важно да се намери правилната част от числото. Но в живота такива случаи са много повече.

Видове фракции: обикновени и десетични

Всички математически фракции са разделени на две големи цифри: обикновени и десетични. Особеностите на първия от тях бяха обсъдени в предишния параграф, така че сега си струва да се обърне внимание на втория.

Десетична стойност е позиционното въвеждане на част от число, което е фиксирано на буквата, разделена със запетаи, без тире или наклонена черта. Например: 0.75, 0.5.

Всъщност, десетичната дроб е идентична с обикновената, но в знаменателя винаги има едно, следвано от нули - оттук и името му.

Числото, предхождащо запетаята, е целочислената част, а всичко след нея е дробно. Всяка проста фракция може да се преобразува в десетична. Така десетичните дроби, посочени в предишния пример, могат да бъдат записани като обикновени: ¾ и ½.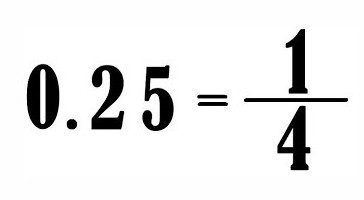

Заслужава да се отбележи, че двата десетични и обикновени части могат да бъдат както положителни, така и отрицателни. Ако те се предхождат от знака "-", тази част е отрицателна, ако "+" е положителна.

Подвид на обикновените фракции

Такива фракции са прости.

• Правилно. Те имат стойността на числителя винаги е по-малка от знаменателя. Например: 7/8. Това е правилна фракция, тъй като числителят 7 е по-малък от знаменателя 8.
• Грешен. В такива фракции или числителят и знаменателят са еднакви (8/8), или по-ниската стойност е по-малка от горната стойност (9/8).
• Смесени. Това е името на правилната част, записана с цяло число: 8 ½. Под него се разбира сумата на този брой и дроби. Между другото, можете просто да го направите да се появи на негово място погрешна фракция. За да направите това, 8 трябва да бъде записано като 16/2 + 1/2 = 17/2.
• Composite. Както подсказва името, те се състоят от няколко частични линии: ½ / ¾.
• Намалено / несъвместимо. Те могат да включват както правилна, така и неправилна част. Всичко зависи от това дали числителят и знаменателят могат да бъдат разделени на един и същ номер. Например, 6/9 е намалена фракция, защото и двата му компонента могат да се разделят на 3 и получавате 2/3. Но 7/9 се отнася до невъзпроизводимо, тъй като 7 и 9 са прости числа, които нямат общ делител и не могат да бъдат намалени.

Подвидове с десетичен знак

За разлика от простата, десетичната дроб е разделена само на 2 типа.

• Финалът получи името си поради факта, че след запетаята има ограничен (краен) брой цифри: 19.25.
• Безкрайната част е число с безкраен брой десетични точки. Например, ако разделите 10 на 3, резултатът ще бъде безкрайна част от 3.333 ...

Освен това на фракции

Малко по-трудно е да се извършват различни аритметични манипулации с фракции, отколкото с обикновени числа. Въпреки това, ако научите основните правила, за решаване на всеки пример с тях няма да бъде трудно.

Така че, за да добавите дялове един към друг, първо трябва да се уверите, че и двата термина имат еднакви знаменатели. За тази цел е необходимо да се намери най-малкият брой, който може да бъде споделен без баланс на знаменателите на номерата на добавките.

Например: 2/3 + 3/4. Най-малкият общ брой за тях ще бъде 12, следователно е необходимо всеки знаменател да съдържа този номер. За това, числителят и знаменателят на първата фракция се умножават с 4, оказва се, че 8/12, продължаваме по същия начин с втория член, но само умножаваме с 3 - 9/12. Сега лесно можете да разрешите примера: 8/12 + 9/12 = 17/12. Получената фракция е погрешна стойност, защото числителят е по-голям от знаменателя. Тя може и трябва да се трансформира в правилното смесено, като раздели 17: 12 = 1 и 5/12.

Ако се добавят смесени фракции, първо се изпълняват действия с цели числа, а след това с частични.

Ако примерът съдържа десетични и обикновени дроби, е необходимо и двете да станат прости, след това да ги въвеждат в същия знаменател и да се добавят. Например, 3.1 + 1/2. Числото 3.1 може да бъде записано като смесена част от 3 и 1/10 или като неправилна фракция - 31/10. Общият знаменател на добавките е 10, така че трябва да умножите числителя и знаменателя 1/2 от 5 последователно, което е 5/10. Тогава лесно можете да изчислите всичко: 31/10 + 5/10 = 35/10. Полученият резултат е невъзвратима редуцирана фракция, привеждаме я в нормална форма, намалявайки с 5: 7/2 = 3 и 1/2, или десетично - 3.5.

Ако добавите 2 знака след десетичната запетая, Важно е десетичната точка да е със същия брой цифри. Ако случаят не е такъв, просто трябва да добавите необходимия брой нули, защото в десетичен знак това може да се направи без сериозни последствия. Например, 3.5 + 3.005. За да разрешите тази задача, трябва да добавите 2 нули към първото число и след това да добавите един по един: 3,500 + 3,005 = 3,505.

Фракционно изваждане

Изваждайки частта, трябва да направите същото като с добавянето: намалено до общ знаменател, извадете един числител от друг, ако е необходимо, преведете резултата в смесена фракция.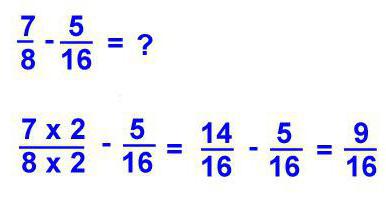

Например: 16 / 20-5 / 10. Общият знаменател ще бъде 20. Необходимо е втората част да се донесе в този знаменател, умножавайки двете му части с 2, оказва се 10/20. Сега можем да решим един пример: 16 / 20-10 / 20 = 6/20. Все пак, този резултат се отнася до редуцируеми дроби, така че си струва да се разделят двете части на 2, а резултатът е 3/10.

Умножение на фракции

Разделянето и умножаването на дроби са много по-прости операции от събирането и изваждането. Факт е, че при изпълнението на тези задачи не е необходимо да се търси общ знаменател.

За да се умножат фракциите, просто трябва да се размножават последователно и двата числителя, а след това и двата знаменателя. Полученият резултат се намалява, ако фракцията е намалена стойност.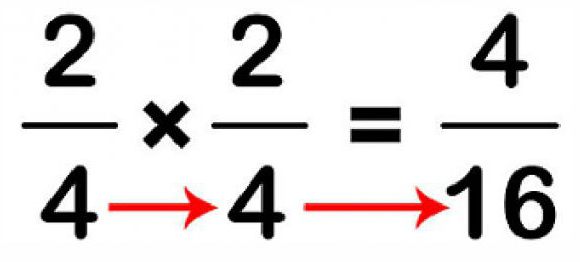

Например: 4 / 9x5 / 8. След алтернативното умножение получаваме резултата 4x5 / 9x8 = 20/72. Такава част се намалява с 4, така че крайният отговор в примера е 5/18.

Как да разделим фракции

Разделянето на фракциите е също така неусложнено действие, всъщност то се свежда до тяхното умножение. За да разделите една фракция с друга, трябва да завъртите втората и да я умножите по първата.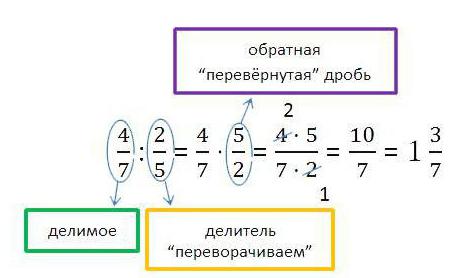

Например делението на фракции 5/19 и 5/7. За да решим един пример, трябва да смените знаменателя и числителя на втората част и да умножите: 5 / 19x7 / 5 = 35/95. Резултатът може да бъде намален с 5 - оказва се 7/19.

В случай, че е необходимо да се раздели фракцията на просто число, методът е малко по-различен. Първоначално е необходимо да се напише този номер като неправилна фракция и след това да се раздели по същата схема. Например, 2/13: 5 трябва да бъде написано като 2/13: 5/1. Сега трябва да обърнете 5/1 и да умножите получената фракция: 2 / 13x1 / 5 = 2/65.

Понякога е необходимо да се направи разделяне на фракции от смесени. Те трябва да правят както с цели числа: да се превърнат в грешни фракции обърнете разделителя и умножете всичко. Например, 8 ½: 3. Превръщаме всичко в нередовни фракции: 17/2: 3/1. Това е последвано от обръщане 3/1 и умножение: 17 / 2x1 / 3 = 17/6. Сега е необходимо да се преведе грешната фракция в правилната - 2 цели и 5/6.

Така че, разбрал какви фракции са и как можете да извършвате различни аритметични операции с тях, трябва да се опитате да не забравите за него. В крайна сметка хората винаги са склонни да разделят нещо на части, отколкото да добавят, така че трябва да сте в състояние да го направите правилно.