Законът на Ампер: формулиране и приложение

Законът на Ампер, чиято формулировка е известна на всеки физик, е една от четирите уравнения на Максуел, които заедно формират основата на цялата теория на класическата електродинамика.

Уравненията на Максуел

Част от закона на Ампер за това как електрическите токове, източниците на магнитни полета, се отнасят до самото поле. С други думи, това (в съчетание с Гаусовия закон за магнетизма) точно описва картината, в която електрическите токове генерират магнитни полета. Корекционната част на Максуел е значителна, защото се казва, че магнитните полета се появяват, когато електрическите полета се променят с времето. Това също е важно, тъй като уравненията на Максуел не са съгласни без него. С корекцията на термина могат да бъдат извлечени формулите спаси електрически заряд и предвиждат съществуването на електромагнитни вълни, които пътуват със скорост.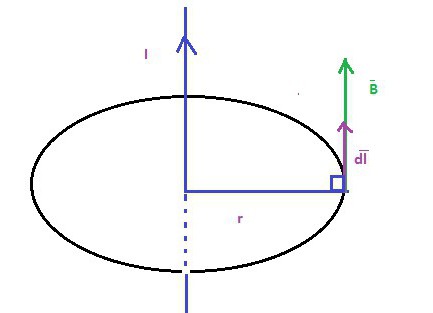

В разбираема форма, законът на Ампер участва, съответно, на линейността на уравненията на Максуел и следователно на цялата теория на класическата електродинамика. Ако вземем два токови разпределителя и ги комбинираме, магнитното поле ще бъде сумата от магнитните полета, произведени от всяка конфигурация.

Контролният елемент на Максуел също е линеен и следователно електромагнитни вълни също са линейни. Те пречат един на друг по принципа на суперпозицията и преминават един до друг без разсейване.

Как да обясним закона на Ампер на прост език?

Най-простото обяснение е, че проводникът носи ток. Ако игнорирате Магнитно поле на Земята може да си представим, че вертикален проводник с електрически ток се издига нагоре.

Хората са склонни да говорят за електромагнетизма, но електричеството е отделено от магнетизма, тъй като е установено, че електричеството и магнетизма влияят един на друг и могат да бъдат комбинирани в система от уравнения. По-специално, в случай на живи проводници електрически ток произвежда магнитно поле. Ориентацията на тези области не е много ясна, но е забележима. Магнитните компаси могат да бъдат поставени около тоководещи проводници, а посоките на полето могат да се видят в посоките на иглените точки.

Възможно е това да се разгледа поради простата симетрия. Токът в проводника произвежда магнитно поле, но какво трябва да се случи с модела в тези полета, ако жицата остава вертикална и се върти под някакъв ъгъл около тази вертикална ос? Факт е, че токът не се променя в никакъв случай при такъв ход. Той все още върви направо. Следователно, това завъртане не може да промени картината на произведеното магнитно поле.

структура

Има само две възможни структури, които ще работят от това. Или полетата са насочени радиално към или от проводника, или около проводника. Първата възможност е хората да получат електрическо поле от електрически зареден проводник. Втората възможност е да получите магнитно поле, създадено от тока през проводниците.

За едно единствено проводниково поле има кръгови структури в центъра на жицата, а силата на полето намалява с разстоянието. Като образец, тя е много подобна на вълните, които се образуват, когато камъкът падне във водата. Има две основни разлики между езерцето и модела на магнитното поле. Първото е, че магнитното поле остава непроменено на дадено разстояние. Тя няма да расте, но ще намалее в дадена точка. Второто е, че магнитното поле има посока към всяка точка на допиране на кръга.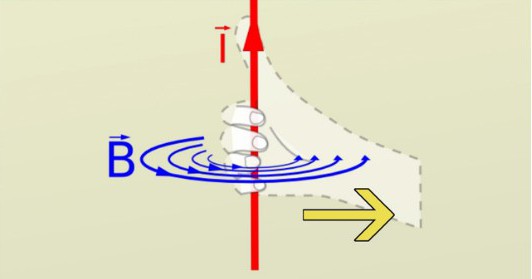

Ток и разстояние

Следващата част от закона на Ампер гласи, че силата на магнитното поле зависи от силата на тока и разстоянието от проводника. Резултатът е, че ако умножите силата на магнитното поле с обиколката на кръга, този продукт ще бъде пропорционален на силата на електрическия ток. Това означава, че ако удвоите разстоянието от проводника, линията на окръжността се удвоява и величината на магнитното поле пада два пъти.

Но законът на Ампер ви позволява да се справяте с токове, които се произвеждат в системи, по-сложни от един проводник. Но всички тези случаи са еквивалентни. Това означава, че идеята силата на магнитното поле умножено по дължината на пътя остава полезно и все още зависи от сумата на всички токове вътре в веригата, която формира пътя.

Как разбирате закона в практически смисъл?

Това включва някои векторни смятания, които могат да бъдат обяснени по интуитивен начин:

• Магнитните полета се създават от електрически токове.
• Магнитните полета се “навиват” върху тока, който ги произвежда в дадена посока.
• Колкото повече ток, толкова по-силно е създадено магнитното поле. Силата на магнитното поле е пропорционална на тока.

Законът на Ампер свързва тези понятия заедно в една от двете математически формули. Полето става по-интензивно, когато се приближава към жицата.

Пропорционалност на общия ток

В интегралната форма на закона на Ампер се използва понятието за линеен интеграл. По принцип, можете да изберете конкретен цикъл (т.е. затворен път през пространството) и да ходите по линия, да добавите компонентите на магнитното поле. Това ще покаже колко магнитно поле се върти около повърхността, ограничена от цикъла. Вярно е твърдението, че това количество е пропорционално на общия ток, който е ограничен от контура.

За да разберете това, трябва да разгледате веригата, ограничаваща проводника. Ако се въртите около проводник, магнитното поле винаги отива в една и съща посока, което означава, че общата сума на криволинейния интеграл ще бъде положителна. Казва, че можете да обиколите тока! В допълнение, можете да определите посоката на тока, като използвате правилото за дясната ръка. Ако текущият поток се движи в различна посока, стойността на криволинейния интеграл е обърната.

Сега можем да приемем, че се прави цикъл, при който не се затваря тел, а се прави кръг обратно на часовниковата стрелка над проводника. Ако вървите около дъното на цикъла, в повечето случаи посоката ще върви нагоре, следователно приносът към интеграла ще бъде отрицателен. Но когато посоката минава около върха на цикъла, в повечето случаи тя ще бъде същата като текущата, така че приносът ще бъде положителен. Той казва, че вътре в цикъла няма нищо (или няма никакъв ток, или течения в противоположни посоки се компенсират взаимно).

диференциал

В диференциална форма, прилагането на закона на Ампер се среща в понятието за къдрици на векторния домейн. Свиването е количествено измерение, векторното поле е „кърлинг“ около дадена точка. Ако вземем по-малки и по-малки цикли около една точка и изчислим криволинейния интеграл, резултатът трябва да бъде приблизително пропорционален на областта на цикъла. Коефициентът на пропорционалност се извива.

Ако вземете цикъл, който не съдържа проводници, интегралът на линията винаги ще бъде нула. Ако веригата се върти по-далеч и по-далеч, тя винаги ще бъде нула. Коефициентът на пропорционалност ще бъде равен на нула, а роторът ще бъде равен на нула (по-точно нулев вектор). Но ако сте вътре в тел, тогава без значение какъв вид на цикъла, той ще получи ток, преминаващ през него. Идеята е, че за една безкрайно малка верига, само плътността на тока в този момент ще бъде “вътре” от нея, и само плътността на тока в тази точка ще определи стойността на криволинейния интеграл. Затова роторът трябва да бъде пропорционален на плътността на тока в дадена точка, тъй като е свързан със стойността на криволинейния интеграл за безкрайно малка верига.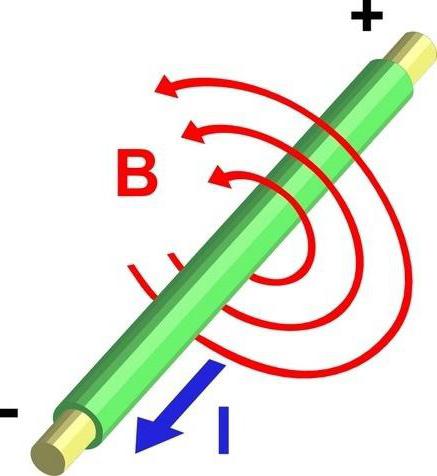

заключение

В диференциални и интегрални форми, законът на Ампер е еквивалентен, той може да бъде показан чрез прилагане на теоремата на Стокс. По същество диференциалната форма е безкрайно малка версия на второто уравнение в "интегрална форма". Но теоремата на Стокс е тема за друго изследване.