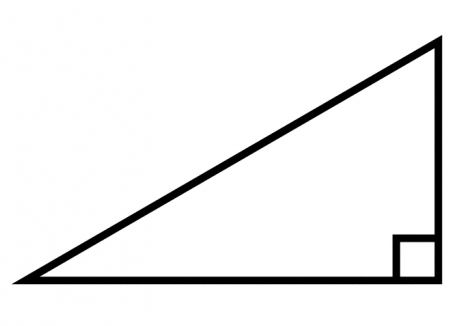
Видове триъгълници. Триъгълни ъгли

Най-простият полигон, който се изучава в училище, е триъгълник. Тя е по-разбираема за учениците и среща по-малко трудности. Въпреки факта, че има различни видове триъгълници, които имат специални свойства.

Каква форма се нарича триъгълник?

Формирани от три точки и отсечки. Първите се наричат ​​върхове, втората - страни. Освен това, всичките три сегмента трябва да бъдат свързани във формата на ъгли между тях. Оттук и името на цифрата "триъгълник".

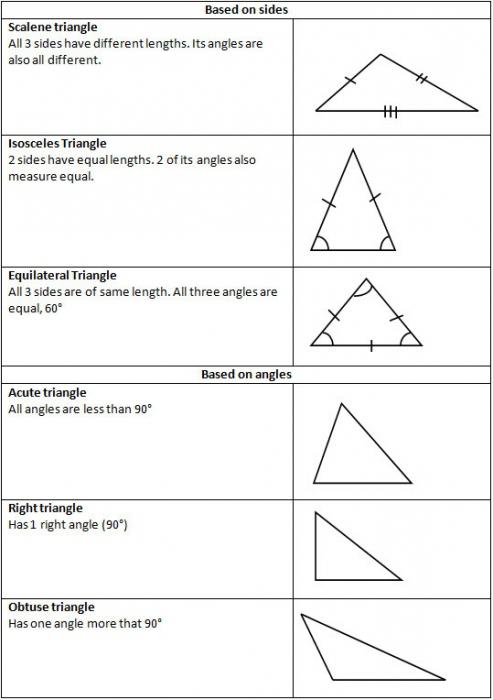
Разлики в имената на ъглите

Тъй като те могат да бъдат остри, тъпи и прави, тогава типовете триъгълници се определят от тези имена. Съответно има три групи такива цифри.

• Първата. Ако всички ъгли на триъгълника са остри, тогава тя ще носи името на остър ъгъл. Всичко е логично.

• Втората. Един от ъглите е тъп, което означава триъгълен ъгъл. Просто няма място.

• На трето място. Има ъгъл от 90 градуса, който се нарича прав. Триъгълникът става правоъгълен.

Разлики в имената на страните

В зависимост от характеристиките на страните, тези типове триъгълници се различават:

• общият случай е многостранен, в който всички страни имат произволна дължина;

• равнобедрени, двете страни на които имат еднакви цифрови стойности;

• равнопоставени, дължините на всички страни са еднакви.

Ако задачата не определя конкретен тип триъгълник, тогава трябва да начертаете произволен тип. В които всички ъгли са остри, а страните имат различна дължина.

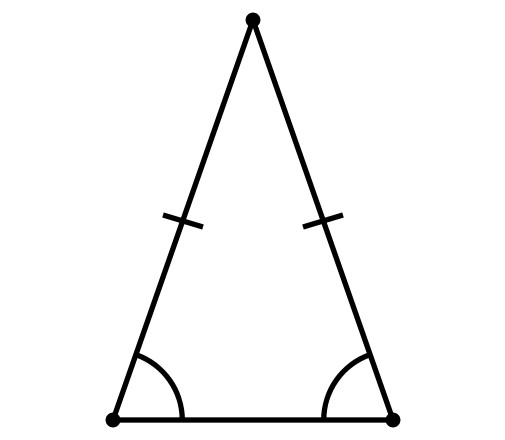
Свойства, общи за всички триъгълници

1. Ако съберете всички ъгли на триъгълника, ще получите число, равно на 180º. И без значение как изглежда. Това правило винаги е валидно.
2. Числената стойност на всяка страна на триъгълника е по-малка от другите две добавени заедно. В същото време, това е повече от тяхната разлика.
3. Всеки външен ъгъл има стойност, която се получава чрез добавяне на две вътрешни, а не съседни на него. Нещо повече, тя винаги е повече от вътрешната, съседна на нея.
4. Срещу по-малката страна на триъгълника винаги има най-малък ъгъл. Обратно, ако страната е голяма, тогава ъгълът ще бъде най-голям.

Тези свойства винаги са валидни, без значение какви триъгълници се разглеждат в проблемите. Всички останали следват от специфичните особености.

Свойства на равнобедрен триъгълник

• Ъглите, които са съседни на основата, са равни.
• Височината, която се държи до основата, е също медианата и ситекторите.
• Височините, медианите и бисектрисите, които са изградени към страните на триъгълника, са съответно еднакви.

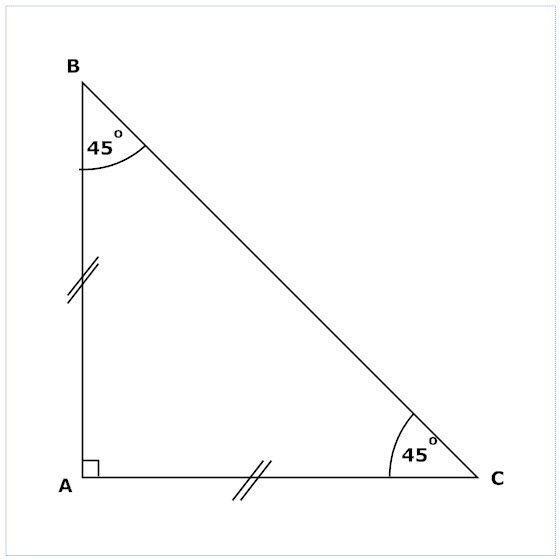
Свойства на равностранен триъгълник

Ако има такава фигура, тогава всички свойства, описани по-горе, ще бъдат верни. Защото равностранечното винаги ще бъде равнобедрено. Но не и обратното, един равнобедрен триъгълник не е задължително да е равностранен.

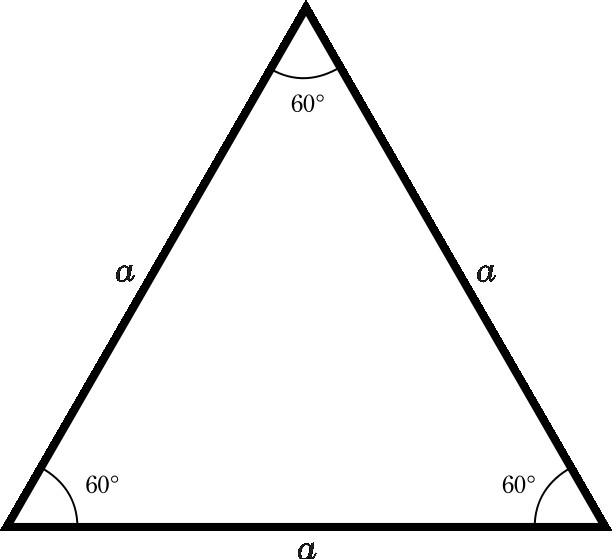
• Всичките ъгли са еднакви и имат стойност 60º.
• Всяка медиана на равностранен триъгълник е неговата височина и симетрия. И всички те са еднакви. За да се определят техните стойности, има формула, която се състои от продукт на партия квадратен корен от 3, разделени на 2.

Свойства на правоъгълен триъгълник

• Два остри ъгъла дават обща стойност от 90 °.
• Дължината на хипотенузата винаги е по-голяма от тази на всеки от краката.
• Числената стойност на медианата, проведена към хипотенузата, е половината от нея.
• Същата стойност е равна на крака, ако е разположена срещу ъгъл от 30º.
• Височината, която се тегли от върха със стойност 90º, има определена математическа зависимост от краката: 1 / n ² = 1 / a ² + 1 / in ² . Тук: a, c - крака, n - височина.

Задачи с различни типове триъгълници

№1. Дава се равнобедрен триъгълник. Неговият периметър е известен и е 90 см. Необходимо е да се познават страните му. Като допълнително условие: страната е по-малка от базата с 1,2 пъти.

решение

Стойността на периметъра е пряко зависима от стойностите, които трябва да бъдат намерени. Сумата от трите страни ще даде 90 см. Сега трябва да си припомним знака на триъгълника, в който той е равнобедрен. Това означава, че двете страни са равни. Можете да направите уравнение с две неизвестни: 2a + b = 90. Тук a е страната, в - базата.

Това е ред на допълнително условие. След него се получава второто уравнение: v = 1,2а. Можете да замените този израз в първия. Оказва се: 2a + 1.2a = 90. След трансформации: 3.2a = 90. От тук a = 28.125 (cm). Сега е лесно да се намери базата. Това се постига най-добре от второто условие: c = 1.2 * 28.125 = 33.75 (cm).

За да проверите, можете да добавите три стойности: 28.125 * 2 + 33.75 = 90 (cm). Точно така.

Отговор: страните на триъгълника са 28,125 cm, 28,125 cm, 33,75 cm.

№2. Страната на равностранен триъгълник е 12 см. Необходимо е да се изчисли височината му.

Решението. За да се търси отговор, достатъчно е да се върнете към точката, в която са описани свойствата на триъгълника. Това е формулата за намиране на височината, медианата и bisector на равностранен триъгълник.

n = a * /3 / 2, където n е височината и a е страната.

Заместването и изчислението дават следния резултат: n = 6 (3 (cm).

Тази формула не трябва да се помни. Достатъчно е да си припомним, че височината разделя триъгълника на две правоъгълни. Освен това се оказва, че е крак, а хипотенузата в него е страната на оригинала, вторият е половината от познатата страна. Сега трябва да напишете Питагоровата теорема и да извлечете формула за височина.

Отговор: височината е 6 cm 3 cm.

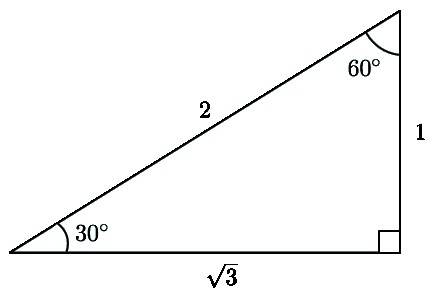
№3. Дава се MKR - триъгълник, 90 градуса, в който се прави ъгъл К. Страните на MR и KR са известни, те са съответно 30 и 15 см. Необходимо е да се определи стойността на ъгъла R.

Решението. Ако направите чертеж, става ясно, че MR е хипотенуза. И това е два пъти повече от КР. Отново трябва да се обърнете към свойствата. Един от тях е свързан с ъгли. От него е ясно, че ъгълът на CMR е равен на 30º. Така желаният ъгъл P ще бъде равен на 60º. Това следва от друго свойство, което гласи, че сумата от два остри ъгъла трябва да бъде 90º.

Отговор: P ъгъл е 60º.

№4. Трябва да намерите всички ъгли на равнобедрен триъгълник. За него е известно, че външният ъгъл от ъгъла при основата е 110º.

Решението. Тъй като е даден само външният ъгъл, това трябва да се използва. Той се формира с вътрешността ъгълът е разгънат. Така че общо те ще дадат 180º. Това означава, че ъгълът в основата на триъгълника ще бъде равен на 70º. Тъй като е равнобедрен, вторият ъгъл има същото значение. Остава да изчислим третия ъгъл. От общото за всички триъгълници свойство сумата на ъглите е 180º. Следователно, третият се определя като 180º - 70º - 70º = 40º.

Отговор: ъглите са 70º, 70º, 40º.

№5. Известно е, че в равнобедрен триъгълник ъгълът, разположен срещу основата, е 90º. Въз основа на маркираната точка. Сегментът, който го свързва с прав ъгъл, го разделя в съотношение от 1 до 4. Трябва да знаете всички ъгли на по-малкия триъгълник.

Решението. Един от ъглите може да бъде идентифициран незабавно. като правоъгълен триъгълник и равнобедрени, тогава тези, които лежат в основата му ще бъдат при 45º, т.е. при 90º / 2.

Вторият от тях ще помогне да се намери известното в състоянието отношение. Тъй като тя е равна на 1 до 4, тогава частите, в които тя е разделена, се получава само 5. Затова, за да откриете по-малкия ъгъл на триъгълник, трябва да получите 90º / 5 = 18º. Остава да научим третата. За да направите това, от 180º (сумата на всички ъгли на триъгълника), извадете 45º и 18º. Изчисленията са прости и ще се окажат: 117º.

Отговор: 18º, 45º, 117º