Ротационно движение на тялото. Закон на въртеливото движение
Тази статия описва важна част от физиката - "Кинематика и динамика на ротационното движение".
Основни понятия за кинематиката на въртене
Ротационно движение материална точка около фиксирана ос се нарича такова движение, траекторията на която е кръг, разположен в равнината, перпендикулярна на оста, и неговият център лежи върху оста на въртене.
Въртящото движение на твърдо тяло е движение, при което всички точки на тялото се движат по концентрични кръгове (чиито центрове лежат на една и съща ос) в съответствие с правилото за въртеливо движение на материална точка.
Нека произволно твърдо тяло Т се върти около оста О, която е перпендикулярна на равнината на фигурата. Изберете точка М на това тяло.По време на въртенето тази точка ще опише окръжност с радиус r около оста О.
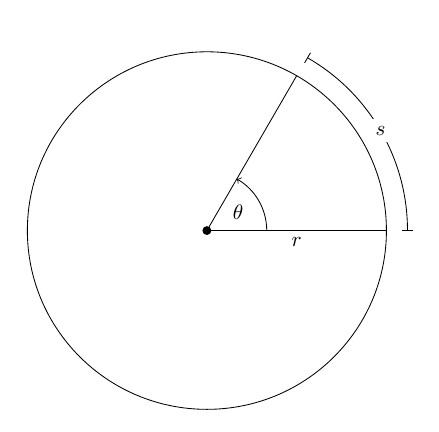
След известно време радиусът ще се върти спрямо началната позиция с ъгъл Δφ.
Посоката на десния винт (по часовниковата стрелка) се приема като положителна посока на въртене. Промяната в ъгъла на въртене с времето се нарича уравнението на въртене на твърдо тяло:
φ = φ (t).
Ако φ се измерва в радиани (1 rad е ъгълът, съответстващ на дъга с дължина, равна на неговия радиус), тогава дължината на дъгата на окръжност ΔS, която материалната точка M ще премине през времето Δt, е равна на:
ΔS = Δφr.
Основните елементи на кинематиката на равномерното въртеливо движение
Една мярка за движение на материална точка в кратък период от време dt е елементарният ротационен вектор dφ .
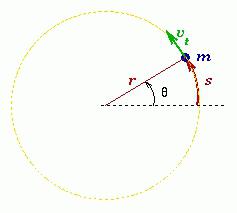
Ъглова скорост Материална точка или тяло е физическа величина, която се определя от съотношението на вектора на елементарното завъртане към продължителността на това завъртане. Посоката на вектора може да се определи чрез правилото на десния винт по оста О. В скаларната форма:
ω = dφ / dt.
Ако ω = dφ / dt = const, тогава такова движение се нарича равномерно въртеливо движение. Когато тя е ъгловата скорост се определя от формулата
ω = φ / t.
Съгласно предварителната формула, измерението на ъгловата скорост
[ω] = 1 rad / s.
Равномерното въртеливо движение на тялото може да се опише чрез периода на въртене. Периодът на въртене T е физическа величина, която определя времето, необходимо на тялото около оста на въртене да извърши една пълна оборота ([T] = 1 s). Ако във формулата за ъгловата скорост приемем t = T, φ = 2 π (пълен обратен радиус r), тогава
ω = 2π / T,
следователно периодът на ротация се определя, както следва:
T = 2π / ω.
Броят на оборотите, които тялото прави за единица време, се нарича честота на въртене ν, която е равна на:
ν = 1 / T.
Честотни единици: [ν] = 1 / c = 1 s -1 = 1 Hz.
Сравнявайки формулите за ъгловата скорост и скоростта на въртене, получаваме израз, отнасящ се до тези величини:
ω = 2πν.
Основните елементи на кинематиката на неравномерното въртеливо движение
Неравномерното въртеливо движение на твърда или материална точка около фиксирана ос характеризира ъгловата му скорост, която се променя с времето.
Векторът ε , който характеризира скоростта на промяна на ъгловата скорост, се нарича вектор на ъглово ускорение:
ε = dω / dt.
Ако тялото се върти, ускорявайки се, т.е. dω / dt> 0 , векторът има посока по оста в същата посока като ω.
Ако въртенето е бавно - dω / dt <0 , то векторите ε и ω са противоположно насочени.
Забележка. При възникване на неравномерно въртеливо движение, векторът ω може да се променя не само по величина, но и по посока (при завъртане на оста на въртене).
Връзката между величините, характеризиращи транслационното и ротационното движение
Известно е, че дължината на дъгата с ъгъла на въртене на радиуса и нейната стойност е свързана с
ΔS = Δφ r.
Тогава линейната скорост на материалната точка, изпълняваща ротационното движение
υ = ΔS / Δt = Δφr / Δt = ωr.
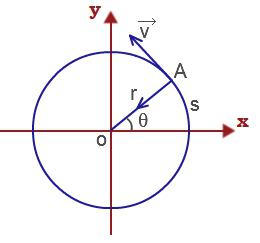
Нормално ускорение на материална точка, която се извършва ротационно движение напред определяме както следва:
a = υ 2 / r = ω 2 r 2 / r.
Така че, в скаларна форма
a = ω 2r.
Тангенциална ускорена материална точка, която извършва въртеливо движение
a = ε r.
Момент на инерция на материална точка
Векторният продукт на радиуса-вектора на траекторията на материална точка на маса m i от неговия инерция се нарича ъгловият момент на тази точка спрямо оста на въртене. Посоката на вектора може да се определи, като се използва правилото с десния винт.
Моментът на инерцията на материалната точка ( L i ) е насочен перпендикулярно на равнината, изтеглена през r i и υ i, и образува с тях десните три вектора (т.е. при преместване от края на вектора r i до υ i, десният винт ще покаже посоката на вектора L i ).
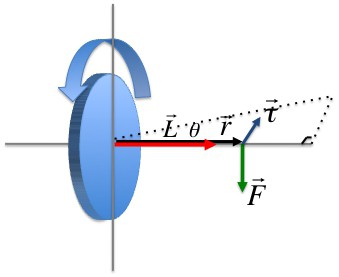
В скаларна форма
L = m i υ i r i sin (υ i , r i ).
Като се има предвид, че при движение в кръг, векторът на радиуса и векторът на линейната скорост за i-тата материална точка са взаимно перпендикулярни,
sin (υ i , r i ) = 1.
Така ъгловият момент на материалната точка за въртеливо движение ще приеме формата
L = m i υ i r i .
Моментът на сила, който действа върху i-та материална точка
Векторният продукт на радиуса-вектора, който се държи в точката на прилагане на силата, се нарича момент на сила, действаща върху i-тата материална точка спрямо оста на въртене.
В скаларна форма
M i = r i F i sin (r i , F i ).
Ако приемем, че r i sinα = l i , Mi i = l i F i .
Стойността на l i, равна на дължината на перпендикуляра, понижена от точката на въртене до посоката на силата, се нарича рамо на силата F i .
Ротационна динамика
Уравнението на динамиката на въртене се записва като:
M = dL / dt.
Формулировката на закона е следната: скоростта на промяна на ъгловия момент на тяло, която се върти около фиксирана ос, е равна на получения момент около тази ос на всички външни сили, приложени към тялото.
Момент на импулс и момент на инерция
Известно е, че за i-тата материална точка ъгловият импулс в скаларна форма е даден от формулата
L i = m i υ i r i .
Ако вместо линейната скорост се замени изразът й през ъгловата:
υ i = ωr i ,
тогава изразът за ъгловия импулс приема формата
L i = m i r i 2 ω.
Количеството i i = m i r i 2 се нарича момент на инерция около оста на i-тата материална точка на абсолютно твърдо тяло, преминаващо през неговия център на масата. Тогава ъгловия момент на материалната точка, който пишем:
L i = I i ω.
Моментът на импулса на абсолютно твърдо тяло се записва като сумата от импулсните моменти на материалните точки, които съставляват това тяло:
L = Iω.
Момент на сила и момент на инерция
Законът за ротационното движение гласи следното:
M = dL / dt.
Известен да представи момента импулс на тялото възможно чрез момента на инерцията:
L = Iω.
след това
M = Idω / dt.
Като се има предвид, че ъгловото ускорение се определя от израза
ε = dω / dt,
получаваме формулата за момента на силата, представена от момента на инерцията:
M = Iε.
Забележка. Моментът на сила се счита за положителен, ако ъгловото ускорение, с което е причинено, е по-голямо от нула, и обратно.
Теорема на Щайнер. Закон за добавяне на инерционни моменти
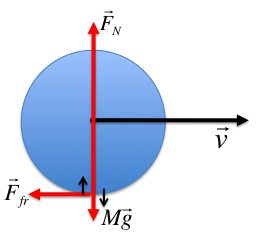
Ако оста на въртене на тялото през център на масата то не минава, тогава по отношение на тази ос можете да намерите неговия момент на инерция съгласно теоремата на Щайнер:
I = I 0 + ma 2 ,
където I 0 - началният момент на инерцията на тялото; m е телесна маса; а е разстоянието между осите.
Ако системата, която се върти около фиксираната ос, се състои от n тела, тогава общият момент на инерцията на този тип система ще бъде равен на сумата от моментите, които го правят (законът за добавяне на моментите на инерция).