Правоъгълен трапец: всички формули и примери за задачи
Задачите с трапец не изглеждат трудни в редица фигури, които са били изследвани по-рано. Като специален случай се разглежда правоъгълен трапецоид. А когато се търси неговата област, понякога е по-удобно да се раздели на две вече познати: правоъгълник и триъгълник. Човек трябва само да помисли малко и има решение.
Определението за правоъгълен трапецоид и неговите свойства
При произволен трапец базите са успоредни и страните могат да имат произволна стойност на ъглите към тях. Ако се вземе под внимание един правоъгълен трапец, то в него една от страните винаги е перпендикулярна на основите. Това означава, че двата ъгъла в него ще бъдат равни на 90 градуса. Освен това те винаги принадлежат към съседни върхове или, с други думи, на една страна.
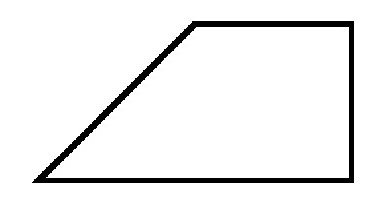
Други ъгли в правоъгълен трапец са винаги остри и тъпи. И сумата им винаги ще бъде равна на 180 градуса.
Всяка диагонал се формира с по-малката си страна правоъгълен триъгълник. А височината, която се изтегля от върха с тъп ъгъл, разделя фигурата на две. Единият е правоъгълник, а другият е правоъгълен триъгълник. Между другото, тази страна винаги е равна на височината на трапеца.
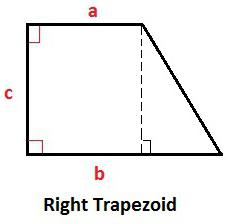
Какви обозначения се приемат във представените формули?
Всички стойности, използвани в различни изрази, които описват трапец, са удобно посочени веднага и са представени в таблицата:
| стойност | Неговото обозначение |
| а | по-голяма база |
| б | по-малка основа на правоъгълен трапец |
| c, h | перпендикулярна на основната страна, височина |
| г | наклонена страна |
| α | остър ъгъл |
| β | тъп ъгъл |
| m | средна линия |
| d 1 | по-малък диагонал |
| d 2 | голям диагонал |
Формули, които описват елементите на правоъгълния трапец
Най-простият от тях се отнася до височината и по-малката страна:
c = h.
Някои формули за тази страна на правоъгълния трапец:
c = d * sinα;
c = (a - b) * tg α;
c = √ (d2 - (a - b) 2 ).
Първият следва от правоъгълен триъгълник. И казва, че кракът до хипотенузата дава синуса на противоположния ъгъл.
В същия триъгълник вторият крак е равен на разликата между две бази. Следователно, вярно е твърдение, което приравнява тангенса на ъгъла към съотношението на краката.
От същия триъгълник може да се извлече формула, основана на познанието на Питагоровата теорема. Това е третият записан израз.
Формули за другата страна могат да бъдат написани. Те са и три:
d = (a - b) / cosα;
d = c / sin α;
d = √ (c 2 + (a - b) 2 ).
Първите две отново се получават от съотношението в същия правоъгълен триъгълник, а второто се извлича от Питагоровата теорема.
Каква формула може да се използва за изчисляване на площта?
Това, което е дадено за произволен трапец. Необходимо е само да се има предвид, че височината е страната, перпендикулярна на основите.
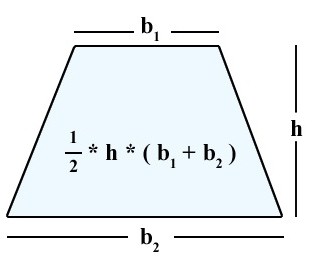
S = (a + b) * h / 2.
Тези стойности не винаги се дават изрично. Следователно, за да се изчисли площта на правоъгълна трапеция, трябва да извършите някои математически изчисления.
Какво ще стане, ако трябва да се изчисли диагоналът?
В този случай трябва да видите, че те образуват два правоъгълни триъгълника. Следователно винаги можете да използвате Питагоровата теорема. Тогава първият диагонал ще бъде изразен като:
d1 = √ (c 2 + b 2 )
или по друг начин, заменяйки „от“ с „h“:
d1 = √ (h 2 + b 2 ).
По същия начин се получават формули за втория диагонал:
d2 = √ (c 2 + b 2 ) или d 2 = √ (h 2 + a 2 ).
Проблем номер 1
Състояние. Площта на правоъгълния трапец е известна и е 120 dm 2 . Височината му е 8 дм. Необходимо е да се изчислят всички страни на трапеца. Допълнително условие е, че една основа е по-малка от другата с 6 dm.
Решението. Тъй като е даден правоъгълен трапец, в който е известна височината, веднага можем да кажем, че едната страна е равна на 8 dm, т.е. по-малката страна.
Сега можете да преброите другите: d = √ (с 2 + (a - b) 2 ). И тук и двете страни и разликата между основите се дават веднага. Последното е 6 dm, това е известно от състоянието. Тогава d ще бъде равно квадратен корен от (64 + 36), т.е. от 100. Така намерихме друга страна, равна на 10 dm.
Сумата от базите може да се намери от формулата за района. Тя ще бъде равна на двойната стойност на областта, разделена на височината. Ако преброите, се оказва, че 240/8, следователно сумата на базите е 30 dm. От друга страна, разликата им е 6 dm. Комбинирайки тези уравнения, можем да изчислим и двете бази:
a + b = 30 и a - b = 6.
Можете да изразите a (b + 6), да го замените в първото равенство. Тогава се оказва, че 2b ще бъде равен на 24. Следователно, просто b ще бъде 12 dm.
Тогава последната страна а е равна на 18 dm.
Отговорът е. Страните на правоъгълния трапецовид: a = 18 dm, b = 12 dm, c = 8 dm, d = 10 dm.
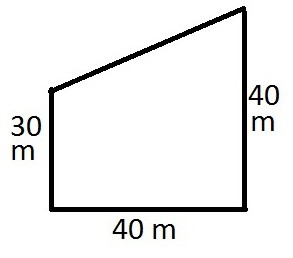
Проблем номер 2
Състояние. Даден е правоъгълен трапец. Голямата му страна е равна на сумата от базите. Неговата височина е 12 см. Изграден е правоъгълник, чиито страни са равни на основата на трапеца. Необходимо е да се изчисли площта на този правоъгълник.
Решението. Трябва да започнете с желаното. Изискваната площ се определя като произведение на a и b. И двете количества не са известни.
Ще бъде необходимо да се използват допълнителни равенства. Един от тях се основава на изявлението от условието: d = a + b. Необходимо е да се използва третата формула за тази страна, която е дадена по-горе. Оказва се: d 2 = c 2 + (a - b) 2 или (a + b) 2 = c 2 + (a - b) 2 .
Необходимо е да се извърши трансформацията, вместо нейната стойност да се замени от условието - 12. След отваряне на скобите и поставяне на такива термини се оказва, че 144 = 4 ab.
В началото на решението се казва, че a * b дава необходимата площ. Следователно в последния израз можете да замените този продукт с S. Едно просто изчисление ще даде стойността на площта. S = 36 cm2.
Отговорът е. Необходимата площ е 36 см 2 .
Проблем номер 3
Състояние. Площта на правоъгълна трапецовидна конструкция 150√3 cm². Острият ъгъл е 60 градуса. Ъгълът между малката основа и по-малкия диагонал има същата стойност. Необходимо е да се изчисли по-малкият диагонал.
Решението. От свойствата на трапецовидните ъгли се оказва, че неговият тъп ъгъл е 120º. Тогава диагоналът го разделя на равни, защото една част от нея вече е 60 градуса. Тогава ъгълът между този диагонал и втората основа също е 60 градуса. Това означава, че триъгълник, оформен от голяма основа, наклонена страна и по-малък диагонал, е равностранен. Така желаният диагонал ще бъде равен на а, както и на страната d = a.
Сега трябва да разгледаме правилния триъгълник. В него третият ъгъл е 30 градуса. Затова кракът, лежащ срещу него, е равен на половината от хипотенузата. Това означава, че по-малката основа на трапеца е равна на половината от желания диагонал: b = a / 2. От него е необходимо да се намери височина, равна на страната, перпендикулярна на основите. Страната тук е крак. От Питагоровата теорема:
c = (a / 2) * .3.
Сега остава само да замести всички стойности в формулата за площ:
150√3 = (a + a / 2) * (a / 2 * )3) / 2.
Решаването на това уравнение дава корен от 20
Отговорът е. По-малкият диагонал е 20 см дълъг.