Поанкаре предположение: история на проблема, доказателство, значение

В училище всеки е запознат с концепциите на теоремата и хипотезата. Като правило най-простите и най-примитивни закони са засегнати в живота, докато математиците правят много сложни предположения и представляват интересни проблеми. Не винаги самите те успяват да намерят решения и доказателства, а в някои случаи техните последователи и просто колеги се борят в продължение на много години.

Институтът по глина през 2000 г. състави списък от 7 така наречените предизвикателства на хилядолетието по аналогия със списъка на хипотезите, съставен през 1900 година. Почти всички тези задачи вече са решени, само един от тях е мигрирал към актуализираната версия. Сега списъкът на проблемите е както следва:

• Хипотезата на Ходж;
• равенство на класове P и NP;
• Хипотеза на Пуанкаре;
• Теория на Ян-Милс;
• Хипотеза на Риман;
• съществуването и гладкостта на решаване на уравненията на Навие-Стокс;
• Предположението на Бърч-Суиннертон-Дайър.

Всички те принадлежат към различни дисциплини в математиката и са важни. Например уравненията на Навие-Стокс се отнасят до хидродинамиката, но на практика те могат да опишат поведението на веществото в земната магма или да бъдат полезни за прогнозиране на времето. Но всички тези проблеми все още търсят тяхното доказателство или отричане. Освен един.

Теорема на Поанкаре

Трудно е да се обяснят с прости думи какъв е проблемът, но можете да опитате. Представете си сфера, например балон. Всички точки на нейната повърхност са на еднакво разстояние от неговия център, който не принадлежи на него. Но това е двуизмерно тяло и хипотезата говори за триизмерно. Вече е невъзможно да си представим, но имаме теоретична математика. В този случай, разбира се, всички точки на това тяло също ще бъдат премахнати от центъра.

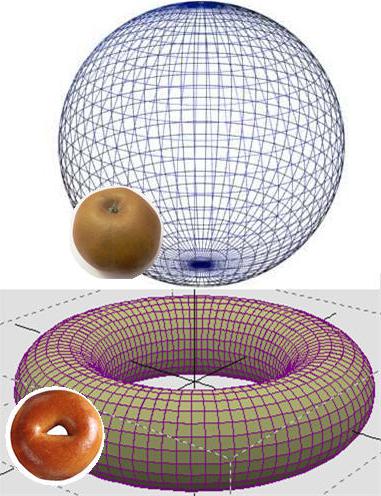
Този проблем се отнася до топологията - науката за свойствата на геометричните форми. И един от основните термини в него е хомеоморфизмът, т.е. висока степен на сходство. За да дадем пример, можете да си представите топка и тор. Една цифра не може да се получи от друга, като се избягват разкъсвания, но конусът, кубът или цилиндърът от първия може да се получи доста лесно. Това е хипотезата на Поанкаре и е посветена на тези метаморфози само с една разлика - говорим за многоизмерно пространство и тела.

История на

Френски математик Анри Пуанкаре изучава различни области на науката. За неговите постижения може да се каже, например, фактът, че съвсем независимо от Алберт Айнщайн, той изложи основните разпоредби специална теория на относителността. През 1904 г. той поставя въпроса за доказване, че всяко триизмерно тяло, което притежава определени свойства на сфера, е точно до деформация. По-късно тя е разширена и обобщена и става специален случай на хипотезата на Търстън, формулирана през 1982 година.

формулировка

Poincaré първоначално остави такова твърдение: всяко просто свързано компактно триизмерно многообразие без граница е хомоморфно на триизмерна сфера. По-късно той беше разширен и обобщен. И все пак за дълго време това беше първоначалната задача, която предизвика най-много проблеми и беше решена само 100 години след появата му.

Тълкуване и смисъл

Това е хомеоморфизъм, вече беше обсъдено. Сега си струва да се говори за компактност и сингулярност. Първото означава само, че сортът има ограничени размери, не може да бъде непрекъснато и безкрайно опъната.

Що се отнася до уникалността, можете да опитате да дадете прост пример. Двуизмерната сфера - ябълката - има едно интересно свойство. Ако вземете обичайната затворена гума и я прикрепите към повърхността, тогава гладката деформация може да бъде намалена до една точка. Това е свойството на уникалността, но да го представяме във връзка с триизмерно пространство доста трудно.

Говорейки просто, проблемът е да докаже, че сингулярността е уникално свойство за сферата. И ако, относително казано, опитът с гумена лента завърши с такъв резултат, то тялото е хомеоморфно към него. Що се отнася до прилагането на тази теория към живота, Поанкаре вярвал, че Вселената в известен смисъл е триизмерна сфера.

Доказателство за

Не мислете, че от десетките математици, които са работили по целия свят, никой не е напреднал с една йота, решавайки този проблем. Напротив, имаше напредък и в крайна сметка доведе до резултат. Самият Поанкаре не е имал време да завърши работата, но неговите изследвания сериозно разшириха цялата топология.

През 1930-те години интересът към хипотезата се върна. На първо място, текстът беше разширен до "n-мерните пространства", а след това американският Уайтхед съобщи за успешни доказателства, а по-късно я изостави. През 60-те и 70-те години двама математици наведнъж - Smale и Stallings - почти едновременно, но по различни начини са разработили решение за всички n по-големи от 4.

През 1982 г., както и за 4, бяха открити доказателства, останаха само 3. В същата година Турстън формулира хипотезата за геометризацията, а теорията на Пуанкаре е нейният конкретен случай.

Тогава работата беше донякъде в застой - американецът Ричард Хамилтън предложил да използва потока Ricci в решението, но той срещнал трудности и не завършил изследването.

В продължение на 20 години хипотезата на Пуанкаре сякаш беше забравена. През 2002 г. руският математик Григорий Перелман представя решение в общи линии, шест месеца по-късно прави някои допълнения. По-късно тези доказателства бяха тествани и донесени до „блясък” от американски и китайски учени. И самият Перелман, изглежда, е загубил всякакъв интерес към проблема, въпреки че решава по-общия проблем на геометризацията, за който предположението на Пуанкаре е само специален случай.

Признаване и оценка

Разбира се, това веднага се превърна в усещане, защото решението на една от проблемите на хилядолетието просто не можеше да се пренебрегне. Още по-изненадващо бе фактът, че Григорий Перелман отказал всички награди и награди, като казал, че вече има прекрасен живот. В съзнанието на обикновените хора той веднага стана пример за този полу-луд гений, който се интересува само от науката.

Всичко това предизвика много дискусии в пресата и медиите, че популярността на математика е станала негова. През лятото на 2014 г. имаше информация, че Перелман отива на работа в Швеция, но това се оказва само слух, той все още живее скромно в Санкт Петербург и почти не комуникира с никого. Сред наградите, които му бяха присъдени, бяха не само наградата Clay Institute, но и престижния Fields Medal, но той отказа всичко. Въпреки това, Хамилтън, който, според пресмятанията на Перелман, е направил не по-малко важен принос към доказателството, също не е забравен. През 2009 и 2011 г. печели и престижни награди и награди.

Културна рефлексия

Въпреки факта, че за обикновените граждани както изявлението, така и решението на този проблем не са много разумни, доказателствата стават известни доста бързо. През 2008 г. японският режисьор Масахито Касуга засне документалния филм "Заклинанието на хипотезата на Поанкаре" по този повод, посветен на неговите 100-годишни опити за решаване на този проблем.

Много математици, участвали в този проблем, взеха участие в стрелбата, но главният герой, Григорий Перелман, не искаше да прави това. Повече или по-малко близки приятели също бяха замесени в стрелбата. Документалният филм, излизащ на екраните след обществения резонанс за отказа на учения да приеме наградата, спечели слава в определени кръгове и получи няколко награди. Що се отнася до масова култура, обикновените хора все още се чудят какви аргументи е водил Петербургският математик, отказвайки да вземе пари, когато може да го даде, например, на благотворителност.