Кинетична енергия - енергията на движението на телата
Потенциалната и кинетичната енергия ни позволяват да характеризираме състоянието на всяко тяло. Ако първото се използва в системи на взаимодействащи се обекти, то последното се свързва с тяхното движение. Тези видове енергия, като правило, се разглеждат, когато силата, свързваща телата, е независима от траекторията на движение. В този случай важни са само началните и крайните позиции.
Обща информация и концепции
Кинетичната енергия на системата е една от най-важните му характеристики. Физиците разграничават два вида такава енергия в зависимост от вида на движението:
• прогресивно;
• ротация.
Кинетичната енергия (E k ) е разликата между общата енергия на системата и останалата енергия. Въз основа на това можем да кажем, че това се дължи на движението на системата. Тялото го има само когато се движи. В покой, обектът е нула. Кинетичната енергия на всяко тяло зависи единствено от скоростта на движение и техните маси. Общата енергия на системата е пряко зависима от скоростта на нейните обекти и разстоянието между тях.
Основни формули
В случай, че някоя сила (F) действа върху тяло, което е в покой по такъв начин, че то влиза в движение, можем да говорим за правене на работа dA. Стойността на тази енергия dE ще бъде по-висока, колкото повече работи. В този случай следващото равенство е вярно: dA = dE.
Като се има предвид пътя, пропътен от тялото (dR) и неговата скорост (dU), може да се използва законът на Нютон 2, въз основа на който: F = (dU / dE) * m.
Горният закон се използва само когато има инерционна референтна система. Има и друг важен нюанс, който се взема предвид при изчисленията. Стойността на енергията се влияе от избора на система. Така, според системата SI, тя се измерва в джаули (J). Кинетичната енергия на тялото се характеризира с маса m, както и скоростта на движение υ. В този случай тя ще бъде: E k = ((υ * υ) * m) / 2.
Въз основа на горната формула можем да заключим, че кинетичната енергия се определя от масата и скоростта. С други думи, тя е функция на движението на тялото.
Енергия в механичната система
 Кинетичната енергия е механична енергия система. Това зависи от скоростта на нейните точки. Дадена енергия всяка материална точка е представена със следната формула: E = 1 / 2mυ 2, където m е масата на точка, а υ е неговата скорост.
Кинетичната енергия е механична енергия система. Това зависи от скоростта на нейните точки. Дадена енергия всяка материална точка е представена със следната формула: E = 1 / 2mυ 2, където m е масата на точка, а υ е неговата скорост.
Кинетичната енергия на механичната система е аритметичната сума от същите енергии на всички нейни точки. Тя може да се изрази и по следната формула: E k = 1 / 2Mυ c2 + Ec, където υc е скоростта на центъра на масата, M е масата на системата, Ec е кинетичната енергия на системата при движение около центъра на масата.
Твърда енергия
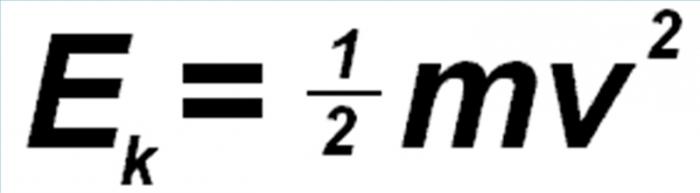 Кинетичната енергия на тялото, която се движи прогресивно, се определя от същата енергия на точка с маса, равна на масата на цялото тяло. За изчисляване на индикатори при движение се прилагат по-сложни формули. Промяната на тази енергия на системата в момента на нейното движение от една позиция в друга се осъществява под влиянието на прилаганите вътрешни и външни сили. Тя е равна на сумата от работата на Aue и A'u на тези сили по време на това движение: E2 - E1 = Au Aue + ∑u A'u.
Кинетичната енергия на тялото, която се движи прогресивно, се определя от същата енергия на точка с маса, равна на масата на цялото тяло. За изчисляване на индикатори при движение се прилагат по-сложни формули. Промяната на тази енергия на системата в момента на нейното движение от една позиция в друга се осъществява под влиянието на прилаганите вътрешни и външни сили. Тя е равна на сумата от работата на Aue и A'u на тези сили по време на това движение: E2 - E1 = Au Aue + ∑u A'u.
Това равенство отразява теоремата за промяната на кинетичната енергия. С негова помощ се решават най-различни проблеми на механиката. Без тази формула е невъзможно да се решат редица важни задачи.
Кинетична енергия при високи скорости
Ако скоростта на тялото е близка до скоростта на светлината, кинетичната енергия на материалната точка може да се изчисли по следната формула:
E = m0c2 / -1-υ2 / c2 - m0c2,
където c е скоростта на светлината във вакуум, m0 е масата на точка, m0c2 е енергията на точка. На ниска скорост (υ При въртенето на тялото около оста всяка от нейните елементарни обеми маса (mi) описва кръг с радиус ri. В този момент обемът има линейна скорост υi. Тъй като се разглежда твърдо вещество, ъгловата скорост въртенето на всички обеми ще бъде същото: ω = υ1 / r1 = υ2 / r2 = ... = υn / rn (1). Кинетичната енергия на въртене на твърдо тяло е сумата от всички същите енергии на нейните елементарни обеми: E = m1υ1 2/2 + miυi 2/2 + ... + mnυn 2/2 (2). Когато използваме израз (1), получаваме формулата: E = Jz ω 2/2, където Jz е моментът на инерцията на тялото около оста Z. Когато се сравняват всички формули, става ясно, че моментът на инерцията е мярка за инерцията на тялото по време на въртеливо движение. Формула (2) е подходяща за обекти, които се въртят около фиксирана ос. Кинетичната енергия на тялото, движещо се надолу по равнината, се състои от енергията на въртене и транслационно движение: E = mυc2 / 2 + Jz ω 2/2, където m е масата на движещото се тяло, Jz е моментът на инерцията на тялото около оста, υc е скоростта на центъра на масата, ω е ъгловата скорост. Промяната в стойността на кинетичната енергия е тясно свързана с потенциала. Същността на това явление може да бъде разбрана чрез закона за запазване на енергията в системата. Сумата от E + dP по време на движението на тялото винаги ще бъде същата. Промяната в стойността на E винаги възниква едновременно с промяна в dP. Така те се трансформират, сякаш се вливат един в друг. Такова явление може да се намери в почти всички механични системи. За изчисляване на енергийната стойност се избира произволен момент (счита се първоначален) и референтна система. Възможно е да се определи точното количество потенциална енергия само в зоната на въздействие на силите, които не зависят от траекторията на тялото при извършване на работа. Във физиката тези сили се наричат консервативни. Те имат постоянна връзка със закона за запазване на енергията. Ако външното влияние е минимално или сведено до нула, изследваната система винаги ще бъде в състояние, при което потенциалната му енергия също ще се стреми към нула. Например, хвърлена нагоре топка ще достигне границата на тази енергия в горната точка на траекторията на движение и в същия момент ще започне да пада. По това време натрупаната енергия в полет се превръща в движение (извършена работа). За потенциалната енергия във всеки случай има взаимодействие на поне две тела (в примера с топка, тежестта на планетата влияе върху нея). Кинетичната енергия може да се изчисли индивидуално за всяко движещо се тяло. Потенциалната и кинетичната енергия се променят изключително във взаимодействието на тела, когато силата, действаща върху тялото, извършва работа, чиято стойност е различна от нула. В затворена система работата на силата или еластичността е равна на промяната в потенциалната енергия на обектите със знака "-": A = - (Ep2 - Ep1). Работата на силата или еластичността е равна на промяната на енергията: A = Ek2 - Ek1. От сравнението на двете уравнения е ясно, че промяната в енергията на обекти в затворена система е равна на промяната в потенциалната енергия и е противоположна на знака: Ek2 - Ek1 = - (Ep2 - Ep1), или по друг начин: Ek1 + Ep1 = Ek2 + Ep2. От това равенство е ясно, че сумата на тези две енергии на тела в затворена механична система и взаимодействащите сили на еластичност и агресия винаги остава постоянна. Въз основа на гореизложеното може да се заключи, че в процеса на изследване на механичната система трябва да се вземе предвид взаимодействието на потенциалната и кинетичната енергия. 
Ротационна енергия на системата
Планарно движение на тялото

Промяната на енергията в механичната система
Енергийна взаимосвързаност
Потенциалните и кинетичните енергии са тясно свързани. Тяхната сума може да бъде представена като общата енергия на системата. На молекулярно ниво това е така вътрешна енергия тяло. Тя присъства постоянно, стига да има поне някакво взаимодействие между телата и топлинното движение. Изборът на референтна система
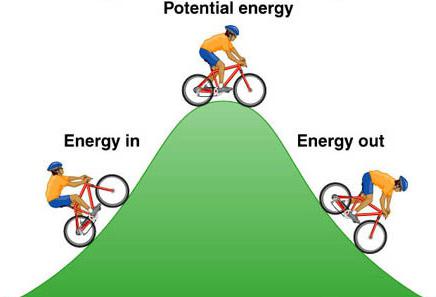
Същността на разликата между потенциалната и кинетичната енергия
Взаимно свързване на различни енергии