Интерполацията е ... Определение, характеристики на изчисленията и примери за интерполация

Много от нас се сблъскаха с непонятни термини в различни науки. Но има много малко хора, които не се страхуват от неразбираеми думи, а напротив, насърчават и ни принуждават да се ровим все повече и повече в изучаваната тема. Днес ще говорим за такова нещо като интерполация. Това е метод за конструиране на графики от известни точки, който позволява, с минимално количество информация за дадена функция, да предвиди поведението му на определени участъци от кривата.

Преди да се обърнем към същността на самата дефиниция и да разкажем по-подробно, разказваме малко за историята.

История на

Интерполацията е известна още от древни времена. Този феномен обаче се дължи на няколко от най-известните математици от миналото: Нютон, Лайбниц и Григорий. Те разработиха тази концепция с помощта на по-напреднали математически методи, налични по това време. Преди това интерполацията, разбира се, беше използвана и използвана в изчисленията, но беше направена в напълно неточни начини, които изискват голямо количество данни за изграждане на модел, който е повече или по-малко близо до реалността.

Днес можем дори да изберем кой метод на интерполация е по-подходящ. Всичко е преведено на компютърен език, който с голяма точност може да предскаже поведението на дадена функция в определена област, ограничена от известни точки.

Интерполацията е доста тясна концепция, следователно историята му не е толкова богата на факти. В следващия раздел ще разберем какво всъщност е интерполацията и как тя се различава от противоположната - екстраполация.

Какво е интерполация?

Както казахме, това е общото име за начините за изграждане на графика по точки. В училище това се прави основно чрез съставяне на таблица, идентифициране на точки на графика и грубо изграждане на линиите, които ги свързват. Последното действие е направено въз основа на съображения за сходството на изследваната функция с другите, вида на графиките, които познаваме.

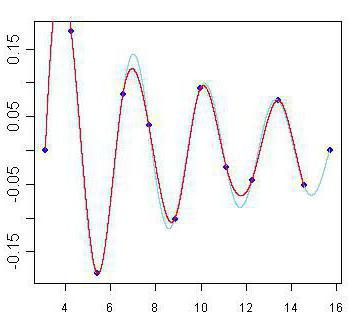
Има обаче и други, по-сложни и точни начини за изпълнение на задачата за начертаване по точки. Така че, интерполацията всъщност е „предсказване“ на поведението на дадена функция в определена област, ограничена от известни точки.

Подобна концепция е свързана със същата област - екстраполация. Той също така представя прогнозата на графиката на функцията, но извън известните точки на графиката. С този метод, прогнозата се прави на базата на поведението на функцията на известен интервал и след това тази функция се прилага и към неизвестния интервал. Този метод е много удобен за практическо използване и активно се използва, например, в икономиката за прогнозиране на възходи и падения на пазара и за прогнозиране на демографската ситуация в страната.

Но ние се отдалечихме от основната тема. В следващия раздел ще разберем каква интерполация се случва и с помощта на кои формули можете да извършите тази операция.

Видове интерполация

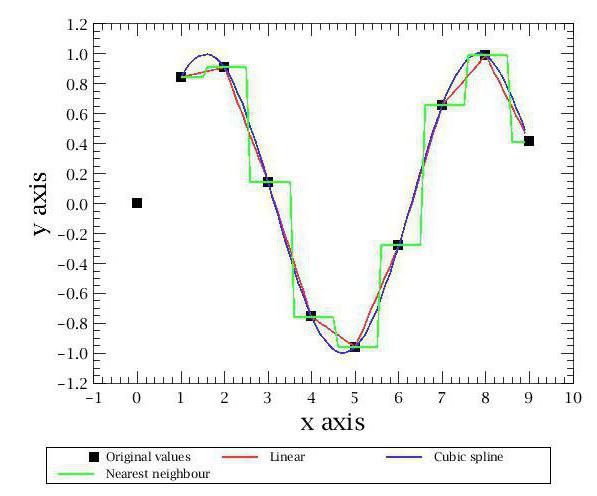
Най-простият тип е интерполацията на най-близкия съсед. С този метод получаваме много приблизителна графика, състояща се от правоъгълници. Ако сте виждали поне веднъж обяснението на геометричния смисъл на интеграла на графиката, тогава ще разберете за какъв вид графична форма говорим.

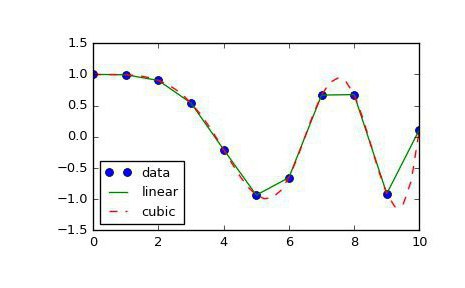
Освен това има и други методи за интерполация. Най-известните и популярни са свързани с полиноми. Те са по-точни и ви позволяват да предскажете поведението на дадена функция с доста слаб набор от стойности. Първият метод на интерполация, който ще разгледаме, ще бъде линейна интерполация от полиноми. Това е най-лесният начин от тази категория и със сигурност всеки от вас го е използвал в училище. Неговата същност е в изграждането на прави линии между известни точки. Както е известно, една права линия минава през две точки на равнината, чието уравнение може да се намери въз основа на координатите на тези точки. Чрез конструирането на тези прави линии се получава счупена графика, която е някак си, но отразява приблизителните стойности на функциите и в общи линии съвпада с реалността. Така се извършва линейна интерполация.

Усложнени видове интерполация

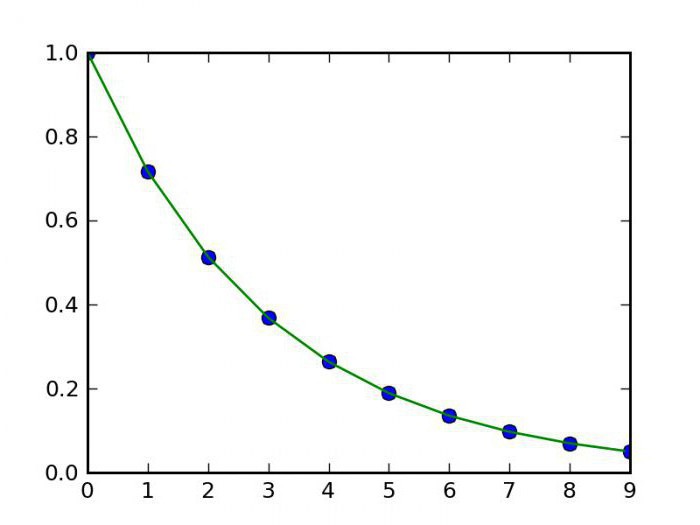
Има по-интересен, но по-сложен метод на интерполация. Той е изобретен от френския математик Джоузеф Луи Лагранж. Ето защо изчислението на интерполация, използвайки този метод, се нарича по него: интерграция на Лагранж. Фокусът тук е следният: ако методът, описан в предходния параграф, използва само линейна функция за изчислението, то деградацията на Лагранж включва и използването на полиноми с по-високи степени. Но не е лесно да се намерят самите формули за интерполация за различни функции. И колкото повече точки са известни, толкова по-точна е формулата за интерполация. Но има и много други методи.

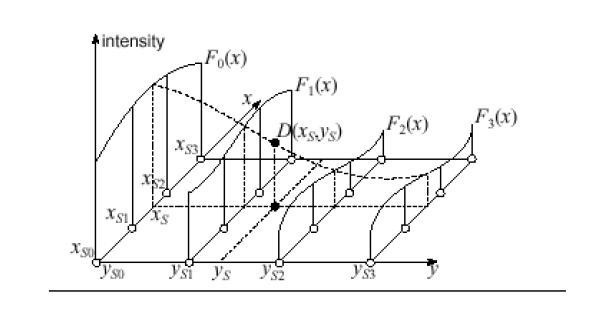
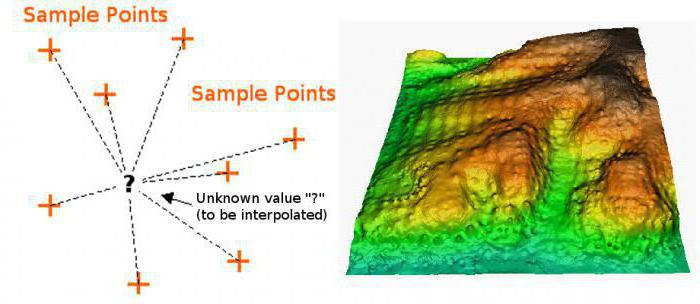
Има и по-съвършен и реалистичен метод на изчисление. Използваната в нея формула за интерполация е набор от полиноми, чието приложение зависи от функционалната област. Този метод се нарича spline функция. Освен това има и начини да се извърши такова нещо като интерполиране на функции на две променливи. Има само два метода. Сред тях билинеарна или двойна интерполация. Този метод ви позволява лесно да изградите графика по точки в триизмерно пространство. Други методи няма да се отразят. Като цяло, интерполацията е универсално име за всички тези графични методи, но разнообразието от начини, по които това действие може да се извърши, ги принуждава да бъдат разделени на групи в зависимост от типа функция, която е предмет на това действие. Това означава, че интерполацията, пример за която разгледахме по-горе, се отнася до директни методи. Има и обратна интерполация, която се различава в това, че ни позволява да изчислим не директната, а обратната функция (т.е. x от y). Няма да разглеждаме най-новите варианти, тъй като това е доста трудно и изисква добра математическа база от знания.

Обръщаме се към един от най-важните раздели. От него научаваме как и къде се прилага наборът от методи, които обсъждаме в живота.

приложение

Математиката е известна като кралицата на науките. Ето защо, дори и да не виждате първо точката в определени операции, това не означава, че те са безполезни. Например, изглежда, че интерполацията е безполезно нещо, с помощта на което могат да бъдат построени само графики, от които малко хора се нуждаят сега. Въпреки това, за всякакви изчисления в инженерството, физиката и много други науки (например биология) е изключително важно да се представи доста пълна картина на явлението, като същевременно има определен набор от ценности. Разпръснатите по графиката стойности не винаги дават ясна представа за поведението на дадена функция в дадена област, стойностите на нейните производни и точките на пресичане с осите. И това е много важно за много области от нашия живот с вас.

И как това е полезно в живота?

На този въпрос е много трудно да се отговори. Но отговорът е прост: няма начин. Това знание няма да ви бъде полезно. Но ако разбирате този материал и методите, по които се извършват тези действия, ще практикувате своята логика, която е много полезна в живота. Основното не е самото знание, а уменията, които човек придобива в процеса на учене. В края на краищата, не е чудно, че има поговорка: "Живей и учи".

Свързани понятия

Можете да разберете за себе си колко важно (и все още не губи своята значимост) тази област на математиката, гледайки на разнообразието на други концепции, свързани с това. Вече говорихме за екстраполация, но има и сближаване. Може би вече сте чули тази дума. Във всеки случай, какво означава това, ние също обсъждахме в тази статия. Апроксимацията, подобно на интерполацията, е концепция, свързана с изграждането на графики на функциите. Но разликата между първата и втората е, че тя представлява приблизителната конструкция на графика, базирана на подобни познати графики. Тези две понятия са много сходни помежду си и е по-интересно да се изучава всеки един от тях.

заключение

Математиката не е толкова сложна наука, колкото изглежда на пръв поглед. Това е доста интересно. И в тази статия ние се опитахме да ви го докажем. Разгледахме понятията, свързани с конструирането на графики, научихме какво е двойна интерполация и разглобихме с примери, където се използва.