Как да намерим областта на триъгълник?
Училищната програма предвижда образованието на децата с геометрия от ранна възраст. Едно от най-основните познания в тази област е да се намери мястото на различни фигури. В тази статия ще се опитаме да въведем всички възможни начини за получаване на тази стойност, от най-простите до най-сложните.
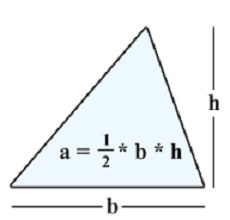
фундамент
Първата формула, която децата учат в училище, включва намирането на площта на триъгълника през дължината на нейната височина и основа. Височината е сегмент, изтеглен от върха на триъгълника под прав ъгъл към противоположната страна, който ще бъде основата. Как да намерим триъгълна зона от тези стойности?
Ако V е височината и O е основата, тогава площта S = V * O: 2.
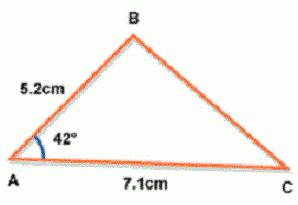
Друга възможност за получаване на желаната стойност изисква да знаем дължините на двете страни, както и величината на ъгъла между тях. Ако имаме L и M са дължините на страните, и Q е ъгълът между тях, тогава можете да получите областта, използвайки формулата S = (L * M * sin (Q)) / 2.
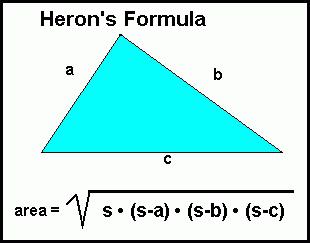
Формула Херон
В допълнение към всички други отговори на въпроса как да се изчисли площта на триъгълник, има формула, която ни позволява да получим нужната стойност, като знаем само дължината на страните. Това означава, че ако знаем дължините на всички страни, тогава не е необходимо да извършваме височината и да изчисляваме нейната дължина. Можем да използваме така наречената формула Херон.
Ако M, N, L са дължините на страните, тогава можем да намерим областта на триъгълника, както следва. P = (M + N + L) / 2, тогава се нуждаем от стойността S2 = P * (PM) * (PL) * (PN). В крайна сметка ще изчислим само корена.
За правоъгълен триъгълник формулата на Херон е малко по-проста. Ако M, L е крак, тогава S = (PM) * (PL).
кръг
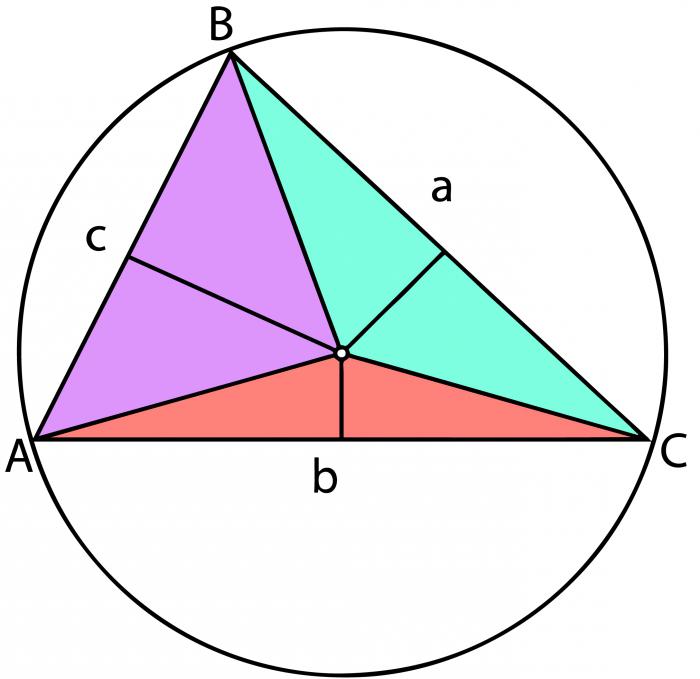
Друг начин да се намери площта на триъгълник е да се използват вписаните и ограничени кръгове. За да получим нужната стойност, използвайки вписания кръг, трябва да знаем неговия радиус. Означаваме го с "r". Тогава формулата, по която ще извършим изчисленията, ще приеме следната форма: S = r * P, където P е половината от сумата на дължините на всички страни.
Най- правоъгълен триъгълник тази формула е малко трансформирана. Разбира се, можете да използвате горното, но е по-добре да използвате друг израз за изчисленията. S = E * W, където Е и W са дължините на сегментите, в които е разделена хипотенузата, точката на допиране на кръга.
Говорейки за обиколката, за да намерите областта на триъгълника също не е трудно. Въвеждайки обозначението R, като радиус на описаната окръжност, можете да получите следната формула, която е необходима за изчисляване на желаното количество: S = (M * N * L) :( 4 * R). Когато първите три стойности са страни на триъгълника.
Говорейки за равностранен триъгълник, благодарение на редица най-прости математически трансформации, може да се получат тъмно модифицирани формули:
S = (3 1/2 * М2) / 4;
S = (3 * 3 1/2 * R2) / 4;
S = 3 * 3 1/2 * r 2 .
Във всеки случай, всяка формула, която ви позволява да намерите зоната на триъгълник, може да бъде променена в съответствие с данните на задачата. Така че всички писмени изрази не са абсолютни. Когато решавате проблеми, помислете дали да намерите най-подходящото решение.
координати
При изучаване на координатните оси задачите, пред които са изправени учениците, стават по-сложни. Въпреки това, не е достатъчно за паника. За да намерите областта на триъгълника по координатите на върховете, можете да използвате същата, но леко модифицирана формула Херон. За координатите той има следната форма:
S = ((x2-x 1 ) 2 * (y 2 -y 1 ) 2 * (z 2 -z 1 ) 2 ) 1/2 .
Въпреки това, никой не забранява, използвайки координатите, да изчисли дължините на страните на триъгълника и след това, използвайки формулите, написани по-горе, да изчисли площта. За да конвертирате координати в дължина, използвайте следната формула:
l = ((x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 ) 1/2 .
бележки
В статията се използва стандартната нотация на стойностите, които се използват в повечето задачи. Степента "1/2" означава, че трябва да извлечете корена от целия израз под скобите.
Когато избирате формула, внимавайте. Някои от тях губят своята значимост в зависимост от първоначалните условия. Например формулата описва кръг. Той може да изчисли резултата за вас във всеки случай, но може да има ситуация, при която триъгълник с дадените параметри може изобщо да не съществува.
Ако седнете вкъщи и си направите домашното, можете да използвате онлайн калкулатора. Много сайтове предоставят възможност за изчисляване на различни стойности за дадени параметри и няма значение кой път. Можете просто да въведете първоначалните данни в полетата и компютърът (уебсайтът) ще изчисли резултата за вас. По този начин можете да избегнете грешки, направени от невнимание.
Надяваме се статията ни да отговори на всички ваши въпроси относно изчисляването на площта на различни триъгълници и няма да се налага да търсите допълнителна информация на друго място. Успех с обучението си!