Как да изчислим процента от сумата на най-простите начини

Всеки човек в живота си почти всеки ден е изправен пред понятието за интерес. А това се отнася не само до получаване на процентна стойност от един номер, но и до решаване на проблема, как да се изчисли процентът на сумата от числата. В ежедневието и ежедневието много хора не обръщат внимание на това, въпреки че всички тези изчисления са включени в нас от училищната пейка.

Какво представлява процентът

Що се отнася до понятието за интерес, то може да бъде обяснено по най-простия начин, без да навлиза в основите на математическите изчисления. Всъщност процентът представлява част от нещо друго. Няма значение в кой показател ще бъде изразена съответствието на процента с основния източник. Основното е да се разбере, че такова представяне може да бъде под формата на самия процент (%) или под формата на част, която в крайна сметка определя съотношението на процентната част към първоначалния вариант.

Използването на интерес в практиката

Как да изчислим лихвите, всеки от нас знае повече от училищния курс по математика. В ежедневието се сблъскваме с проценти почти всяка минута. Всяка домакиня, която приготвя ястие, използва рецепта, в която се представя процентът. Най-простият пример: вземете половин чаша мляко ... Това е математическата интерпретация на това, което представлява определена част по отношение на цялото.

Абсолютно всички изчисления се основават на 100% (100%) или едно (1), ако изчислението ще бъде направено с помощта на фракции. От това и отблъскват при изчисляване на който и да е компонент на първоначалния индикатор.

Същото важи и за въпроса как да се изчисли процентът от сумата, когато първоначалният (100%) показател не е едно число, а няколко. Изчислението тук може да бъде доста голямо. Помислете за най-основните.

Изчислете процента по пропорция

Сега няма да вземем предвид изчисляването на лихвите, използвайки същите таблици на офис програми като Excel, които правят това в автоматичен режим, когато определят подходящата формула.

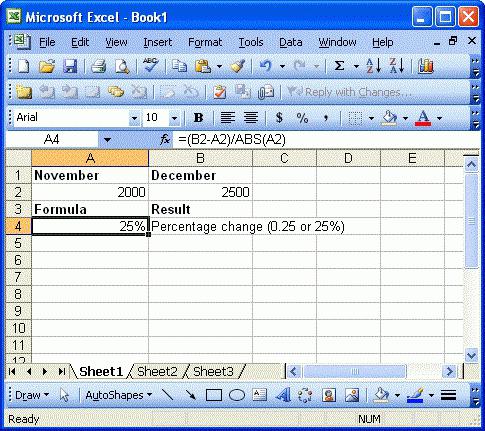
В някои случаи се използва калкулатор, където можете да зададете изчисленията на такива действия. Но сега не става въпрос за това.

Разгледайте най-често срещаните методи за изчисление, познати от училищния курс по математика.

Най-простият и най-често срещаният начин е да се решат пропорциите.

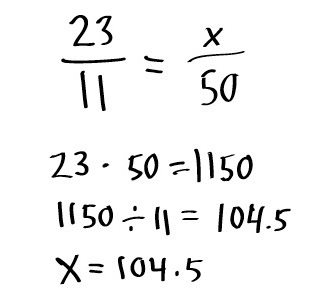
В този случай първоначалният номер е 100% (да речем някакъв произволен номер “а”), а неговата част (да речем, “б”) - като неизвестна “x”. В математиката изглежда така:

а = 100%;

b = x.

Въз основа на правилата за пропорционалност, можете да изчислите неизвестното число x. За целта се използва т.нар. Кръстосан метод. С други думи, трябва да умножите b с 100 и да го разделите с a. Точно същото правило се прилага, ако в случай на съставяне на пропорцията промените b и x на места, когато процентът е известен, но трябва да изчислите частта в цифров израз.

Бързо изчисляване на лихви

Разбира се изчисляване на лихви с помощта на съотношението е фундаментално. Въпреки това, като се използват частични числа, тази процедура се опростява до невъзможност. В крайна сметка, какво е 50% наистина? Половината. Това е 1/2 или 0.5 (въз основа на първоначалния номер 1). Сега е ясно: за да изчислим половината, трябва да умножим желания номер с 1/2, или с 0.5, или да го разделим на 2. Този метод обаче е подходящ само за числа, които са делими без остатък.

В случай на остатъчни или безкрайни знаци в периода след запетая, например 0.33333333 ... е по-добре да се използват частични изрази като 1/3. Между другото, фракциите (в някои случаи ирационални) точно отразяват самото число, тъй като периодичните цифри след запетая, без значение колко питате, няма да даде цяло число. И така една и съща една трета ясно и ясно изразява същността.

В същите рецепти, разбира се, една трета може да се определи, така да се каже, на око. Но в химичните процеси, особено тези, свързани с фината дозировка на компонентите, например във фармацевтичната индустрия, този метод няма да работи. Няма нужда да разчитате на окото. Необходимо е да се използват точни съотношения на съставките, дори ако един от индикаторите има формата на число с число в даден период или е представен под формата на една и съща ирационална фракция. Но, като правило, например, когато се претегля, такива числа могат да бъдат ограничени до десетична точка след десетичната точка или максимум до една хилядна.

Как да се изчисли процентът от сумата

Много често човек трябва да се справи с няколко необходими номера или тяхната сума. Въпросът как да се изчислят процентите на сумата се решава толкова лесно, колкото в случай на използване на един първоначален номер. Единственото нещо, което трябва да се обмисли в този случай е обичайното представяне на сумата като единична стойност.

Например, имаме две числа, a и b, а първоначалният индикатор е числото d. В този случай делът ще бъде както следва:

d = 100%;

(a + b) = x.

Имайте предвид, че сумата (a + b) все още може да бъде представена като едно число. Нека да е z. В случая, когато зададем формулата a + b = z, делът поема изцяло стандартна форма:

d = 100%;

z = x.

Както можете да видите, нищо сложно за него.

Има и друга възможност, когато сумата (a + b) = 100%, и d = x.

Тук решението изглежда така:

(dx 100) / (a ​​+ b) или (d / (a ​​+ b)) + 100 / (a ​​+ b).

Както вече беше разбрано, тук се използва принципът за общ знаменател за дроби.

Ако добавим a и b, сумата от която е равна на z, тогава делът отново се връща към стандартната форма:

z = 100%;

d = x.

Същото важи и в обратен ред.

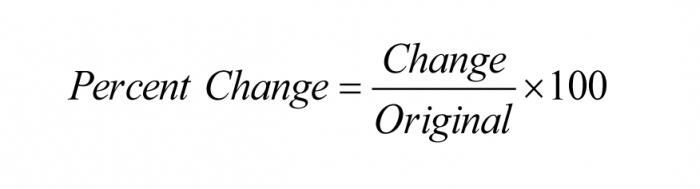
Математическо обяснение

От гледна точка на математиката и нейните основи, решаването на проблема как да се изчисли процент от сума намалява само до прилагането на най-простите правила за разширяване на скобите при умножаване на сумата с едно число и търсене на общ знаменател, който като цяло е такъв. С други думи, тя може да бъде представена с формула, както следва:

ax (b + c) = ab + ac ,

където ab и ac са продукти на термини в скоби (b и c) с число (коефициент) преди скоби a.

Всъщност същият метод действа пропорционално. Да предположим, че имаме определено число z, което представлява 100%, и сумата от числата a и b. Процентът, който се изчислява, се обозначава с неизвестен номер y. В това изпълнение пропорцията приема формата:

z = 100%;

(a + b) = y.

Оттук и простото решение:

((a + b) x 100%) / z = ((ax 100%) + (bx 100%)) / z

В скоби се предприемат действия, за да се подчертае, че операцията по умножение се извършва на първо място, а добавянето на произведения - във втория. Същото действие се извършва, ако първоначално сумата от числата е 100%.

Обратно изчисление

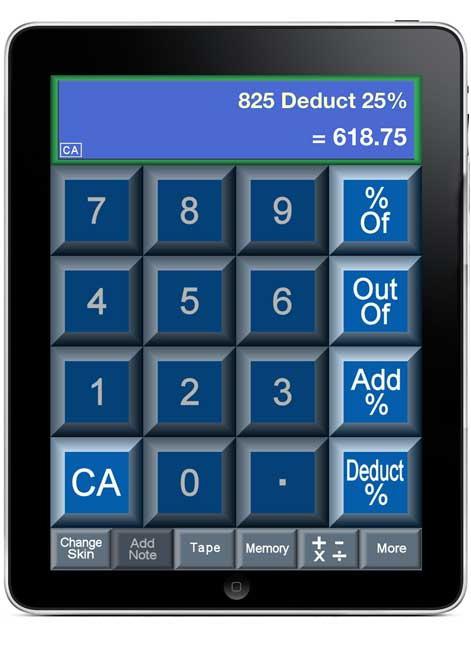
Много често в въпроса как да се изчисли процентът на сумата, има еднозначен обратен трансфер. На практика това се дължи, например, на обратното изчисление на тримесечието. Всеки знае, че тази цифра е 25% от първоначалния брой. Нека например цената на стоките се увеличи с 25%, което възлиза на 25 рубли. Трябва да разберем колко е станал този продукт. Сега ще се опитаме да разберем как да изчислим не първоначалния номер, знаейки процентната стойност, а цялата сума, която трябва да се окаже в края. Изглежда, че решението е просто:

25 = 25% (1/4 или 0.25);

х = 100%.

Не, абсолютно грешно. Така можете да получите само първоначалния номер, с изключение на 25%. За да се изчисли цялата сума, като се вземат предвид 25%, трябва да се използва формулата:

25 = 25%;

х = 100% + 25%.

Или 100 / 0.8, което ще покаже стойността 125 (100 + 25), тъй като 100% плюс 25% в единичното изражение е числото 1.25 (един плюс една четвърт), а в обратната (1 / x) е само 0.8. Изчислявайки, получаваме x = 125.

заключение

Както виждате, няма какво особено трудно да се изчисли процентът на сумата. Вярно е, че в училищната програма обратният превод често се пропуска по някаква причина. Тогава много счетоводители, работещи по доклади, плащащи един и същ ДДС, често имат проблеми.

Така че просто трябва да вземете предвид основните правила за изчисляване на лихвите и проблемите ще изчезнат сами.

От друга страна, за удобство, двете пропорции и използването на фракции могат да се прилагат еднакво. В първия случай имаме, така да се каже, класическата версия, а във втория - просто и универсално решение. Отново, по-добре е да го използвате в случай на разделяне без остатък. Но при изчисляване на най-популярните части като половин, четвърт, трети и т.н., този метод е много удобен.

Обратните изчисления, както се вижда от горните примери, също не са сложни. Основното нещо е да се вземе предвид обратния коефициент при изчисляване на желания брой. Изглежда, че сега всичко е на мястото си. Както се казва, проста математика.