Как да изчислим границите на последователностите?
Математиката е наука, която изгражда света. Като учен и просто човек - никой не може да го направи без него. Първо, малките деца се учат да преброяват, след това добавят, изваждат, умножават и разделят, писмени означения влизат в игра в гимназията, а в по-старите, те не могат да направят без тях.
Но днес ще говорим за това, върху какво се гради цялата известна математика. На общността на числата, наречена "граници на последователността".
Какво представляват последователностите и къде е тяхната граница?
Смисълът на думата "последователност" не е труден за тълкуване. Това е изграждането на неща, в които някой или нещо е подредено в определен ред или опашка. Например, опашката за билети в зоопарка - е поредица. И това може да бъде само едно! Ако, например, да погледнете на опашката в магазина - това е една последователност. И ако един човек внезапно напусне тази линия, това е друга линия, друг ред.
Думата "лимит" също се тълкува лесно - това е краят на нещо. Въпреки това, в математиката, границите на последователностите са тези стойности на числовата линия, към която се стреми поредица от числа. Защо търси и не свършва? Всичко е просто, цифровата линия няма край и повечето от последователностите, като лъчите, имат само началото и изглеждат така:
x 1 , x 2 , x 3 , ... x n ...
Следователно дефиницията на последователност е функция на естествения аргумент. По-просто казано, това е поредица от членове на някой набор.
Как се изгражда числова последователност?
Най-простият пример за числова последователност може да изглежда така: 1, 2, 3, 4, ... n ...
В повечето случаи, за практически цели, последователностите са изградени от числа, а всеки следващ член от поредицата, обозначен с X, има собствено име. Например:
x 1 - първият член на последователността;
х2 - вторият член на последователността;
x 3 - третият член;
...
x n е n-тият срок.
В практическите методи, последователността е дадена от общата формула, в която има някаква променлива. Например:
X n = 3n, тогава числовите серии ще изглеждат така:
х 1 = 3;
х2 = 6;
х 3 = 9;
и така нататък
Не трябва да забравяте, че в общия запис на последователности можете да използвате всякакви латински букви, а не само X. Например: y, z, k и т.н.
Аритметична прогресия като част от последователностите
Преди да търсим границите на последователностите, е препоръчително да се потопим по-дълбоко в самата концепция на такава цифрова поредица, която всички срещат, докато са в средните класове. Аритметичната прогресия е серия от числа, в които разликата между съседни членове е постоянна.
Задачата: “Нека a 1 = 15, а стъпката на прогресията на числова серия d = 4. Създайте първите 4 члена от тази поредица. "
Решение: а 1 = 15 (по условие) - първият член на прогресията (числови серии).
a 2 = 15 + 4 = 19 е вторият член на прогресията.
и 3 = 19 + 4 = 23 - третия член.
a 4 = 23 + 4 = 27 е четвъртият член.
Въпреки това, този метод е труден за достигане на големи стойности, като напр. Специално за такива случаи е получена подходяща за практиката формула: a n = a 1 + d (n - 1). В този случай a 125 = 15 + 4 (125-1) = 511.
Видове последователности
Повечето от последователностите са безкрайни, заслужава си да си спомните за цял живот. Има два интересни типа поредица от числа. Първата се дава с формулата a n = (- 1) n . Математиците често наричат тази последователност мигаща. Защо? Проверете числовите серии.
-1, 1, -1, 1, -1, 1 и т.н. При такъв пример става ясно, че числата в последователностите могат лесно да бъдат повторени.
Факториална последователност. Лесно е да се отгатне - факториал присъства във формулата, която определя последователността. Например: a n = (n + 1)!
След това последователността ще изглежда така:
a 1 = 1x2 = 2;
a2 = 1x2x3 = 6;
a 3 = 1x2x3x4 = 24 и т.н.
Последователност, дефинирана от аритметична прогресия, се нарича безкрайно намаляваща, ако се наблюдава неравенството -1 за всички нейни членове.
a 1 = - ½;
a 2 = ¼;
a 3 = - 1/8 и т.н.
Има дори една последователност, състояща се от един и същ номер. И така, n = 6 се състои от безкрайно множество от шестици.
Определяне на границата на последователност
Границите на последователностите отдавна съществуват в математиката. Разбира се, те заслужават своя компетентен дизайн. Така че, време да научите дефинирането на границите на последователностите. Първо, разгледайте подробно границата за линейна функция:
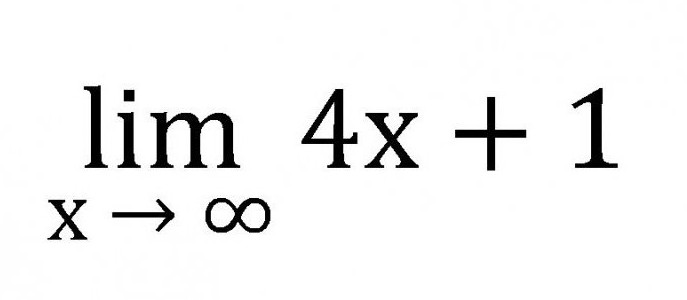
- Всички граници са съкратени lim.
- Граничният запис се състои от абревиатура lim, някаква променлива, насочена към определено число, нула или безкрайност, както и от самата функция.
Лесно е да се разбере, че дефиницията на границата на последователността може да бъде формулирана по следния начин: това е определен брой, към който безкрайно се приближават всички членове на последователността. Един прост пример: a x = 4x + 1. Тогава самата последователност ще изглежда така.
5, 9, 13, 17, 21 ... x ...
Така, тази последователност ще нараства безкрайно и следователно нейната граница е равна на безкрайността при x → и това трябва да бъде записано, както следва:
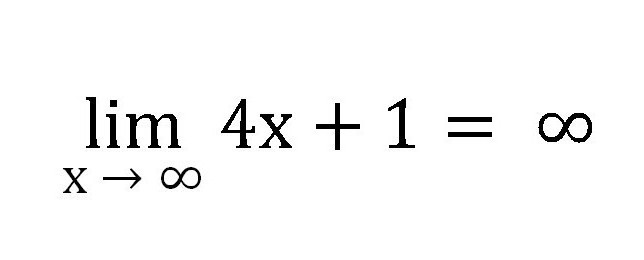
Ако вземем подобна последователност, но x ще има тенденция към 1, получаваме:
a x = 4x + 1.
Серия от числа ще бъде така: 1.4, 1.8, 4.6, 4.944 и така нататък. Всеки път трябва да замествате числото все по-близо до едно (0.1, 0.2, 0.9, 0.986). От тази серия е ясно, че границата на функцията е пет.
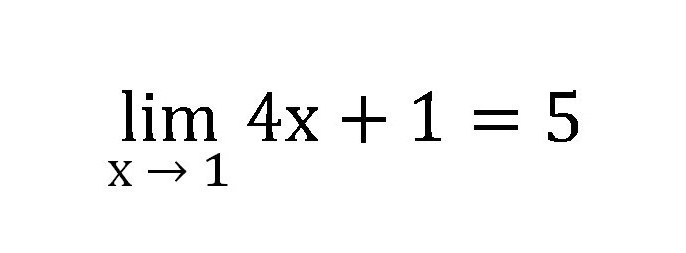
От тази част си струва да си припомним каква е границата на цифровата последователност, дефиницията и метода за решаване на прости задачи.
Общо означение на границата на последователностите
След като изследваме границата на цифрова последователност, нейната дефиниция и примери, можем да преминем към по-сложна тема. Абсолютно всички граници на последователностите могат да бъдат формулирани с една формула, която обикновено се анализира през първия семестър.
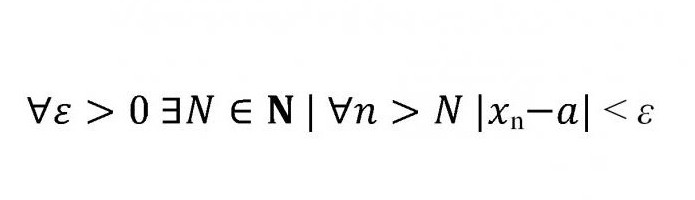
И така, какво означава този набор от букви, модули и знаци за неравенство?
∀ - квантор на универсалност, заместващ изразите „за всички“, „за всички“ и т.н.
∃ - квантор на съществуването, в този случай означава, че има някаква стойност N, принадлежаща на множеството естествени числа.
Дългата вертикална пръчка, следваща N, означава, че даден набор от N е "такъв, че". На практика това може да означава "такова, че", "такова, че" и т.н.
След това идва модулът. Очевидно е, че един модул е разстояние, което по дефиниция не може да бъде отрицателно. Така модулът на разлика е строго по-малък от "епсилон".
За да консолидирате материала, прочетете формулата на глас.
Несигурност и определеност на границата
Методът за намиране на границата на последователностите, който беше обсъден по-горе, е прост в използването, но не е толкова рационален на практика. Опитайте се да намерите лимита за такава функция:
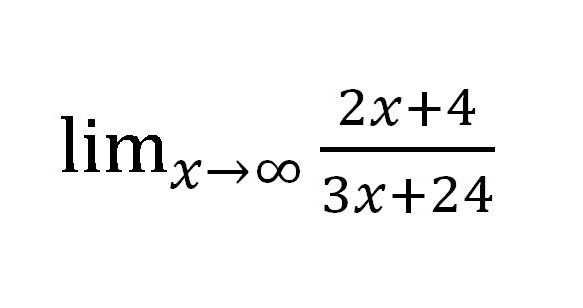
Ако заменим различни стойности на "X" (всеки път нарастващ: 10, 100, 1000 и т.н.), то в числителя получаваме ∞, но в знаменателя също ∞. Оказва се, че е доста странна фракция: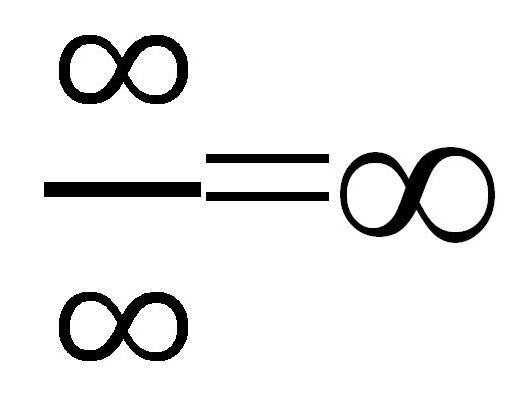 
Но наистина ли е? Изчислете границата на цифровата последователност в този случай изглежда доста лесно. Би могло да се остави всичко, каквото е, защото отговорът е готов и е приет при разумни условия, но има и друг начин специално за такива случаи.
Първо, намираме най-високата мощност в числителя на една фракция - тя е 1, тъй като х може да бъде представена като x 1 .
Сега намираме най-високата сила в знаменателя. Също така 1.
Разделяме числителя и знаменателя на променлива в най-висока степен. В този случай фракцията се дели на x 1 .
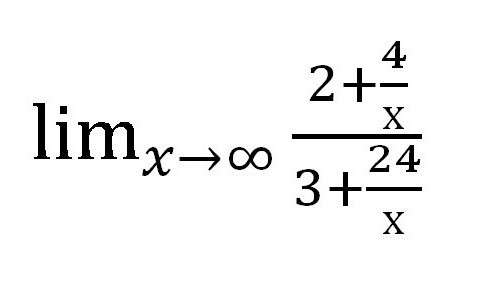
След това ще открием каква стойност има всяка добавка, съдържаща променливата. В този случай, частта. При x → ∞ стойността на всяка от фракциите е с нула. Когато се прави писмена работа, си струва да се направят такива бележки под линия:
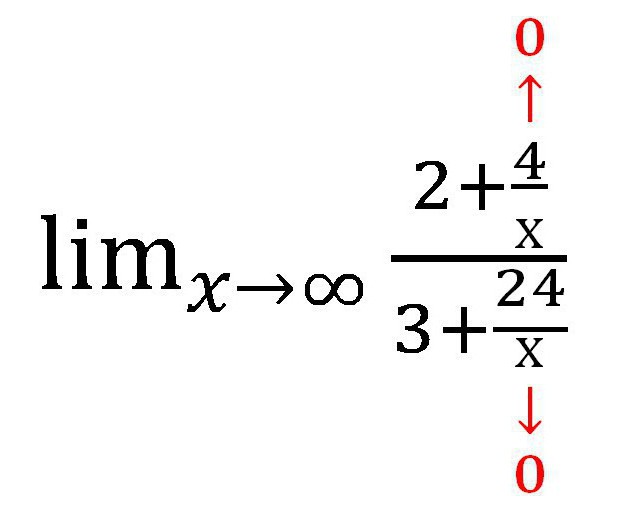
Получава се следният израз:
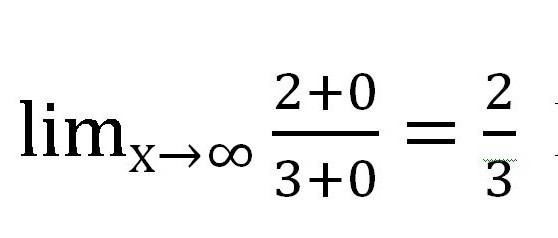
Разбира се, фракциите, съдържащи х, не станаха нули! Но тяхната стойност е толкова малка, че е напълно разрешено да не се вземе предвид при изчисляването. В действителност, x в този случай никога няма да бъде равно на 0, тъй като нула не може да се раздели.
Какво е квартал?
Да предположим, че един професор разполага със сложна последователност, дадена, очевидно, от не по-малко сложна формула. Професорът намери отговора, но дали е подходящ? В края на краищата всички хора грешат.
Огюст Коши в своето време измисли чудесен начин да докаже границите на последователностите. Методът му се наричаше оперативен квартал.
Да предположим, че има някаква точка а, нейната околност в двете посоки на числовата линия е ε ("епсилон"). Тъй като последната променлива е разстоянието, стойността му е винаги положителна.
Сега ще дефинираме някаква последователност x n и ще приемем, че десетият член на последователността (x 10 ) влиза в квартала на. Как да напиша този факт в математическия език?
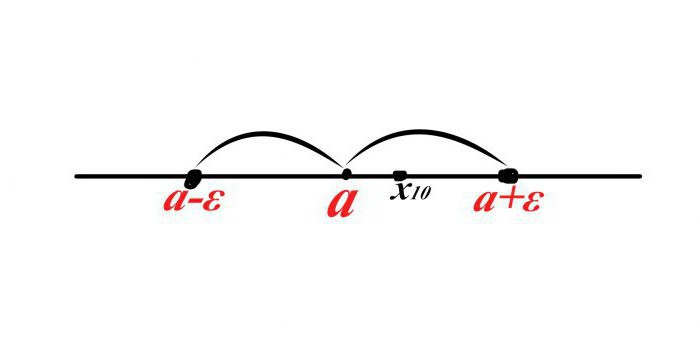
Да предположим, че x 10 е вдясно от точка a, тогава разстоянието е x 10 - a <ε, обаче, ако поставите „X десетата“ вляво от точка a, то разстоянието ще бъде отрицателно, но това е невъзможно, тогава трябва да добавите лявата част на неравенството към модула. Получаваме | x 10 –a | <ε.
Сега е време да изясним на практика тази формула, която беше спомената по-горе. Определено число a е правилно наречено крайна точка на последователността, ако за което и да е от неговите граници неравенството ε> 0 е изпълнено, и целият квартал има собствено естествено число N, така че всички членове на последователността с по-значими числа ще бъдат в последователността | x n - a | <ε ,
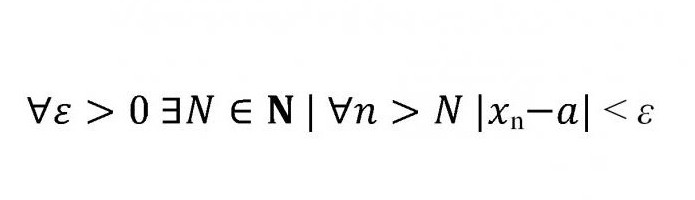
С такива знания е лесно да се приложи решение на границите на една последователност, да се докаже или опровергае готов отговор.
теорема
Теоремите за границите на последователността са важен компонент на теорията, без които практиката е невъзможна. Има само четири основни теореми, които помнят, че е възможно понякога да се улесни хода на решение или доказателство:
- Уникалността на границата на последователността. Ограничението за всяка последователност може да бъде само едно или никакво. Същият пример с опашката, която може да има само един край.
- Ако серия от числа има граница, тогава последователността на тези числа е ограничена.
- Границата на сумата (разликата, произведението) на последователностите е равна на сумата (разликата, произведението) на техните граници.
- Границата на частното от разделянето на две последователности е равна на частното на границите, ако и само ако знаменателят не изчезва.
Доказателство за последователности
Понякога е необходимо да се реши един обратен проблем, за да се докаже дадена граница на числова последователност. Помислете за пример.
Докаже, че границата на последователността, дадена от формулата, е нула.
Според правилото, обсъдено по-горе, за всяка последователност трябва да се изпълни неравенството | x n - a | <ε. Заменете определената стойност и отправна точка. Получаваме:
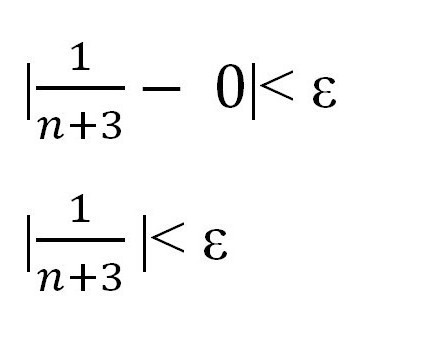
Изразете n чрез "епсилон", за да покажете съществуването на определен брой и докажете съществуването на ограничителна последователност.
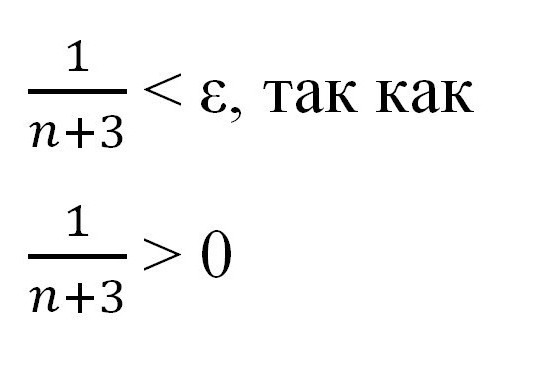
На този етап е важно да се припомни, че "епсилон" и "ен" са положителни и ненулеви числа. Сега можете да продължите по-нататъшни трансформации, като използвате познанията за неравенствата, получени в гимназията.
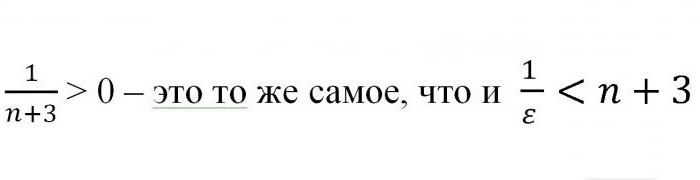
Оттук се оказва, че n> –3 + 1 / ε. Тъй като си струва да си припомним, че говорим за естествени числа, резултатът може да се закръгли, като се постави в квадратни скоби. По този начин беше доказано, че за всяка стойност на квартала "епсилон" на точката а = 0 съществува такава стойност, че първоначалното неравенство се запазва. От това можем спокойно да кажем, че числото a е границата на дадена последователност. Какво трябваше да докаже.
С такъв удобен метод може да се докаже границата на цифрова последователност, колкото и сложна да изглежда на пръв поглед. Основното нещо - не се паникьосвам при вида на работата.
Или може би не е?
На практика съществуването на ограничителна последователност е по избор. Можете лесно да намерите такива серии от числа, които наистина нямат край. Например, същата светкавица x n = (–1) n . очевидно е, че една последователност, състояща се само от две числа, циклично повтаряща се, не може да има граница.
Същата история се повтаря с последователности, състоящи се от едно число, дробно, като в хода на изчисленията несигурността на който и да е ред (0/0, ∞ / ∞, 0/0 и т.н.). Трябва обаче да се помни, че се извършва и погрешно изчисление. Понякога границата на последователностите ще помогне да се провери отново собствените им решения.
Монотонна последователност
По-горе сме разгледали няколко примера на последователности, методи за тяхното решаване и сега ще се опитаме да вземем по-конкретен случай и да го наречем “монотонна последователност”.
Дефиниция: справедливо е да се нарече всяка последователност монотонно нарастваща, ако за нея се държи строгото неравенство x n <x n +1. Също така, всяка последователност с право се нарича монотонно намаляване, ако неравенството x n > x n +1 е за него .
Наред с тези две условия има и сходни слаби неравенства. Съответно, x n <x n + 1 (не намаляваща последователност) и xn > xn + 1 (не-нарастваща последователност).
Но това е по-лесно да се разбере с примери.
Последователността, дадена с формулата x n = 2 + n, образува следната поредица от числа: 4, 5, 6 и т.н. Това е монотонно нарастваща последователност.
И ако вземем x n = 1 / n, ще получим серия: 1/3, ¼, 1/5 и т.н. Това е монотонно намаляваща последователност.
Граница на конвергентна и ограничена последователност
Ограничена последователност - последователност, която има граница. Сходната последователност е поредица от числа, която има безкрайно малка граница.
Така, границата на ограничената последователност е валидна или сложно число. Не забравяйте, че може да има само едно ограничение.
Границата на сходната последователност е безкрайно голямо (реално или сложно). Ако начертаете диаграма на последователността, тогава в даден момент тя ще изглежда като сближаваща се, за да се стреми да се обърне към определена стойност. Оттук и името - конвергентна последователност.
Монотонен лимит
Границата за такава последователност може или не може да бъде. На първо място е полезно да се разбере кога е то, от което може да се отблъсне, когато докаже липсата на граница.
Сред монотонните последователности се излъчват сходни и дивергиращи. Конвергирането е последователност, която се формира от множеството x и има реално или сложно ограничение в множеството. Дивергент - последователност, която няма ограничение в своя набор (нито реален, нито сложен).
Освен това, последователността се слива, ако нейното геометрично изображение се слива с горната и долната граница.
Границата на сходната последователност в много случаи може да бъде равна на нула, тъй като всяка безкрайно малка последователност има известна граница (нула).
Без значение каква сходна последователност, всички те са ограничени, но не всички ограничени последователности се събират.
Сумата, разликата, произведението на две сходни последователности е също конвергентна последователност. Въпреки това, коефициентът може да бъде сходен, ако е дефиниран!
Различни действия с ограничения
Границите на последователностите са съществени (в повечето случаи) като числата и цифрите: 1, 2, 15, 24, 362 и т.н. Оказва се, че някои операции могат да се извършват с ограничения.
Първо, като числа и числа, границите на всяка последователност могат да бъдат добавяни и изваждани. Въз основа на третата теорема за границите на последователностите е валидно следното равенство: границата на сумата от последователности е равна на сумата от техните граници.
Второ, въз основа на четвъртата теорема за границите на последователностите, следващото равенство е вярно: границата на произведението на n-то число на последователностите е равна на произведението на техните граници. Същото важи и за разделението: границата на коефициента на две последователности е равна на частното от техните граници, при условие че границата не е нула. В крайна сметка, ако границата на последователностите е равна на нула, тогава получаваме разделяне с нула, което е невъзможно.
Свойства на последователността
Изглежда, че границата на цифровата последователност вече е анализирана в някои подробности, но такива фрази като „безкрайно малки“ и „безкрайно големи“ числа се споменават повече от веднъж. Очевидно, ако има последователност 1 / x, където x → ∞, тогава такава фракция е безкрайно малка и ако последователността е една и съща, но границата се стреми към нула (x → 0), тогава фракцията става безкрайно голямо. И такива количества имат свои собствени характеристики. Свойствата на границата на последователност, която има всякакви малки или големи стойности, са както следва:
- Сумата от произволно малки количества също ще бъде малко количество.
- Сумата от произволен брой големи количества ще бъде безкрайно голямо количество.
- Продуктът на произволно малки количества е безкрайно малък.
- Продуктът на произволен брой големи числа е безкрайно голяма стойност.
- Ако оригиналната последователност се стреми към безкрайно голямо число, тогава количеството, противоположно на нея, ще бъде безкрайно малко и ще се стреми към нула.
Всъщност изчисляването на границата на една последователност не е толкова трудна задача, ако знаете прост алгоритъм. Но границите на последователностите - тема, която изисква максимално внимание и постоянство. Разбира се, достатъчно е само да уловим същността на решението на такива изрази. Започвайки от малки, с течение на времето можете да достигнете големи върхове.