Как да изчислим ъглите между линия и равнина?
При изучаването на училищния курс по геометрия в двуизмерното пространство се отделя много време за разглеждане на поведението на правите линии. Когато се обръщат към изучаването на стереометрията в горните класове, темата на равнините и правите линии в пространството излизат на преден план. Тази статия разглежда един от тези въпроси. А именно темата за изчисляване между равнини и прави ъгли и разстояния.
Права линия на равнина и методи за нейното задаване
За да се решат успешно изчислителните задачи между правите и равнините на ъгли и разстояния, е необходимо да се научите как да зададете математически тези геометрични обекти, както и да усвоите методите за работа със съответните уравнения. Започваме със задаване на линии в равнината.
Всеки ученик знае следната формула:
y = k * x + b
Работата с нея е доста удобна в двуизмерното пространство. Лесно е да се използва за начертаване на права линия в правоъгълна координатна система. Освен това, познаването на коефициента k за всяка от тях ни позволява да кажем дали те ще бъдат успоредни, или дали се пресичат (за паралелни, техните коефициенти k са равни).
Ако напишем даденото изражение в малко по-различна форма, тогава получаваме формула от общ тип за права линия. Формата й е както следва:
A * x + B * y + C = 0
Очевидно, използвайки прости преобразувания, можете да получите първия израз от него.
Писмените формули могат да се използват и за изчисляване на ъгъла на пресичане на правите линии. Това обаче изисква редица трансформации, което е неудобно. Следователно, когато задачата изисква намиране на ъгъл, за предпочитане е да се използва векторната форма на представяне на линията. Нейният изглед може да бъде написан като:
(x; y) = (x 0 ; y 0 ) + λ * (a; b)
При това равенство координатите X и Y с индекси нула описват позицията на дадена точка, през която минава линията. Стойностите на a и b са координатите на вектора, който лежи върху него. Тя може да бъде насочена едновременно в една посока, а в другата - правината не се променя. Този вектор се нарича водещ вектор, тъй като той уникално определя разпределението на права линия в равнината. Lambda λ е параметър, който взема произволна стойност от множеството реални числа.
Отбелязваме, че векторната форма на записа е забележителна, която ясно съдържа насочен сегмент от права линия, чиито координати се използват за определяне на ъгъла между две прави линии на равнината.
Права линия в триизмерно пространство
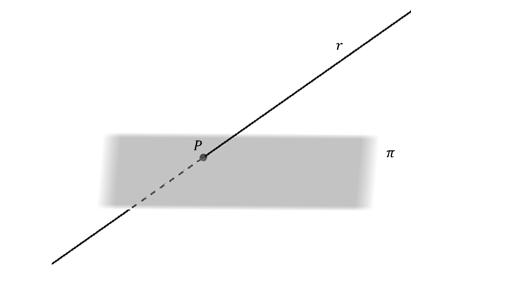
В пространството, описано от трите координатни оси, правната линия се дефинира като обща пресечна точка на равнините. Тук, като се има предвид темата на статията, ние разглеждаме само векторното уравнение. Той е подобен на този за плоския случай, но с добавянето на третата координата:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + λ * (a; b; c)
Когато решавате проблеми, този израз е удобен за отваряне и се прилага в параметрична форма:
x = x 0 + λ * a;
y = y 0 + λ * b;
z = z 0 + λ * c
Забележете, че стойността на параметъра λ, макар и произволна, ще зависи от всичките три равенства.
Описание на самолета
Що се отнася до линията, за равнината има и много начини за нейното определяне. Помислете само за две от тях, които са важни, за да можете да решавате проблемите на практика.
Първият метод на задание е да се въведе уравнение от общ тип. То е подобно на съответния израз за права линия в двумерния случай:
A * x + B * y + C * z + D = 0
Комбинацията от първите три коефициента е координатите на вектора на посоката за тази равнина. По правило се обозначава със символа п, т.е.
n¯ = (A; B; C)
Четвъртият коефициент D определя разстоянието между паралелни равнини, имащи първите три еднакви коефициента.
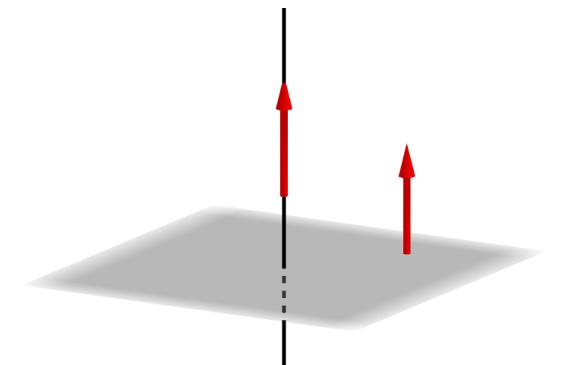
Тъй като векторът n on лежи на нормата към равнината, той е перпендикуляр на абсолютно всеки вектор и права линия, конструирани върху нейните произволни две точки. Познаването на координатите на n¯ е ключово при определяне между правите и ъглите на ъглите.
Вторият начин за определяне на равнината е векторно-параметрична форма на уравнението. Написано е по следния начин:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + λ * (a 1 ; b 1 ; c 1 ) + γ * (a 2 ; b 2 ; c 2 )
Това равенство отразява факта, че две прави линии еднозначно определят равнината в пространството. Тук вторият и третият термин означават два вектора на посоката за произволни прави линии, принадлежащи на равнината.
Нормалният вектор n¯ не се съдържа изрично за тази форма на писане, но е лесно да се изчисли:
n¯ = [(a 1 ; b 1 ; c 1 ) * (a 2 ; b 2 ; c 2 )]
Ъгъл между правите линии
Ако векторните равенства за всяка от правите линии са известни, тогава ъгълът между тях е лесен. За да направите това, трябва само да използвате свойствата на скаларния продукт за направляващите сегменти на правите линии. Ако векторните ръководства са обозначени със символите v и u¯, тогава необходимата формула ще приеме формата:
α = arccos (| (v¯ * u¯) | / (| v¯ | * | u¯ |)))
Тъй като при пресичането на правите се образуват два чифта равни ъгли, тогава се взема остър ъгъл като истински ъгъл между тях. Поради тази причина формулата съдържа знака на модула в числителя.
Тази формула за двуизмерен случай винаги е валидна. Резултатът от 0 о казва, че правите линии не се пресичат, а са паралелни.
Що се отнася до случая в пространството, в допълнение към изчислението по формулата е необходимо да се извършат допълнителни изчисления. Те са свързани с намирането на пресечната точка на въпросните обекти. Факт е, че в пространството може да се получи крайната стойност на ъгъла а, но правите линии няма да се пресичат, тъй като те могат да бъдат пресечени.
Равнина, линия и ъгъл на тяхното пресичане
За да се намери ъгълът между права и равнина, достатъчно е да се знае уравнението за всеки от тези обекти. Ъгълът между тях е ъгълът на две пресичащи се линии, единият от които е оригиналът, а другият принадлежи на равнината и е проекция на оригиналната линия върху нея. Фигурата по-долу показва равнината, която се пресича под ъгъл α.
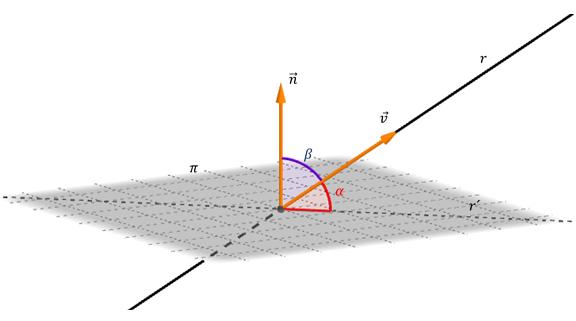
Ако насочващият вектор за директен вектор е обозначен с v¯, а нормата към равнината е n¯ (виж фиг.), То тогава изчисляването на ъгъла α се извършва по формулата:
α = arcsin (| (v¯ * n¯) | / (| v¯ | * | n¯ |))
Отбележете, че в тази формула, за разлика от подобен израз за две пресичащи се прави, се използва функцията arcsine, а не функцията на косинуса.
Разстоянието между правите линии на равнина и равнина и права линия в пространството
За да се изчисли разстоянието между въпросните обекти в геометрията има набор от формули. Прилагането на израз от него зависи от формата, в която са дадени равнината и линията.
Ако две равни линии са дадени в обща форма на равнина, то разстоянието между тях може да се изчисли, както следва:
d = | A * x 1 + B * y 1 + C | / √ (A 2 + B 2 )
Тук x 1 и y 1 са координатите на произволна точка на една права линия, а коефициентите A, B, C се вземат за другата права линия. Тази формула е валидна, ако линиите са успоредни един на друг. Ако се пресичат, разстоянието е нула.
Разстоянието между линията и пресичащата го равнина е нула. Ако правата линия е успоредна на равнината, тогава съответното разстояние се изчислява като:
d = | A * x 1 + B * y 1 + C * z 1 + D | / √ (A 2 + B 2 + C 2 )
Когато координатите принадлежат на произволна точка от линията.
Задача: определете ъгъла между права линия и равнина
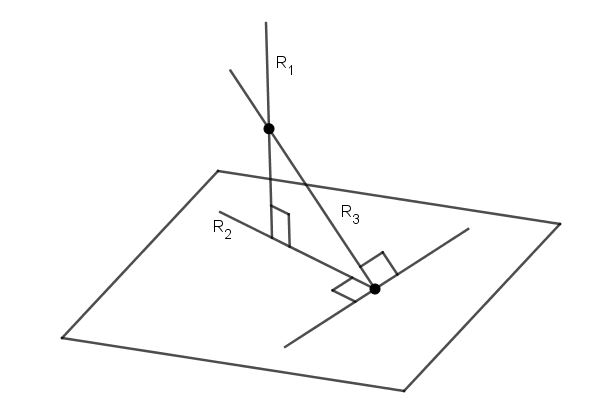
Дадена права линия и равнина:
(x; y; z) = (1; 2; 0) + λ * (- 1; 1; 4);
-5 * x + y - 3 = 0
Какъв е ъгълът между права линия и равнина?
Пишем ръководствата на вектора v и n¯:
v = (-1; 1; 4);
n¯ = (-5; 1; 0)
Заменя ги в подходящата формула за α, получаваме:
α = arcsin (| 5 + 1 + 0 | / (*18 * √26)) ≈ 16,1 o
Задача: да се намери разстоянието между правите линии
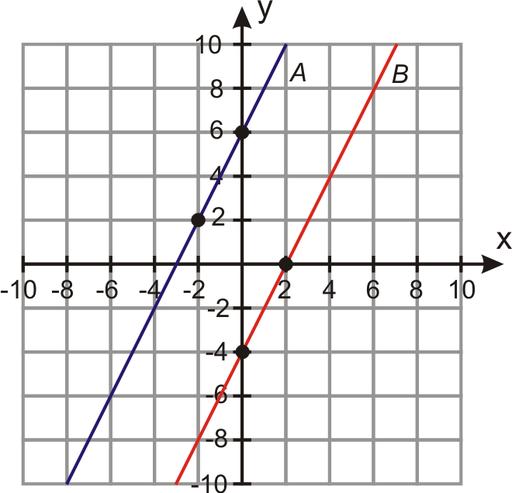
Дадени са две уравнения на прави линии в двумерно пространство:
у = 3 * х - 1;
y = 3 * x + 3
Какво е разстоянието между тях?
Тъй като коефициентите k за двата обекта са едни и същи (равен на 3), случаят с успоредни прави линии.
За да изчислите разстоянието между тях, вземете произволна точка от първата права и пренапишете второто уравнение като цяло, имаме:
координати на точката (0; -1);
3 * x - y + 3 = 0, т.е. A = 3, B = -1, C = 3
Сега тези стойности могат да бъдат заменени с подходяща формула:
d = | 3 * 0 -1 * (- 1) + 3 | / √ (9 +1) = 4 / √10 ≈ 1,265
Отговорът се получава в единици на тази координатна система.