Четири формули, чрез които можете да изчислите площта на ромб. Диамантени свойства

Ромб е специална фигура в геометрията. Поради специалните си свойства не съществува нито една, а няколко формули, с помощта на които се изчислява площта на ромб. Какви са тези свойства и какви са най-често срещаните формули за намиране на областта на тази цифра? Нека видим.

Коя геометрична форма наречен диамант

Преди да разберете каква е площта на ромб, си струва да знаете каква е цифрата.

От времето на евклидовата геометрия ромът се нарича симетричен четириъгълник, всичките четири страни на който са равни по дължина и паралелни по двойки.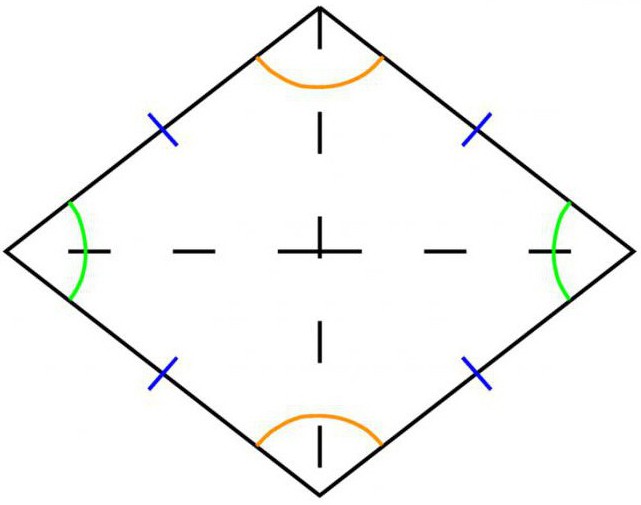

Произход на термина

Името на тази фигура достига до най-модерните езици от гръцки чрез посредничеството на латински. "Прародителката" на думата "ромб" се превърна в гръцкото съществително μόμβος (тамбурин). Въпреки че обитателите на двадесети век, свикнали с кръгли тамбури, трудно могат да си представят различна форма, но елините традиционно правят тези музикални инструменти не кръгли, а ромбовидни.

В повечето съвременни езици този математически термин се използва, както на латински: rombus. Въпреки това, на английски език, диаманти понякога се наричат ​​диамант (диамант или диамант). На тази фигура е дадено такова прозвище поради специалната си форма, наподобяваща скъпоценен камък. По правило такъв термин не се използва за всички диаманти, а само за онези, чийто ъгъл на пресичане между двете му страни е шестдесет или четиридесет и пет градуса.

За първи път тази цифра е спомената в писанията на гръцкия математик, който е живял през първия век на нова епоха - чапла на Александрия.

Какви свойства има тази геометрична фигура?

За да намерите областта на ромб, първо трябва да знаете какви характеристики има тази геометрична фигура.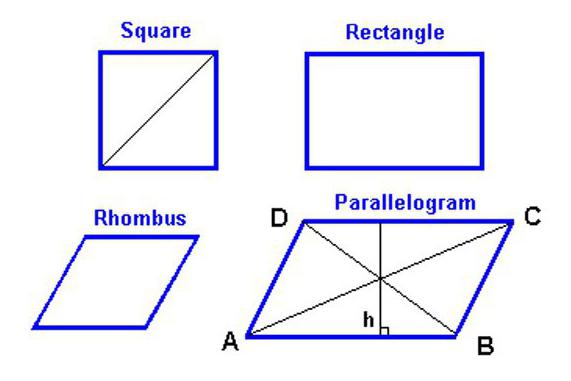

• Както вече споменахме в определението за ромб, това е четиристранно. И заради това, че противоположните й страни са успоредни една на друга по двойки, ромбът също може да се нарече успоредник, което означава, че повечето от свойствата на тази фигура се отнасят за него.
• И двата диагонални ромба в точката на пресичане са равномерно разделени на две. И поради факта, че се пресичат под ъгъл от деветдесет градуса, диагоналите разделят фигурата на 4 правоъгълен триъгълник.
• Във всеки ромб диагоналите разделят ъглите му на две, като в същото време са и бисектриси.
• Ако всяка от двете диагонали на ромб е повишена до силата на квадрат, тогава тяхната сума ще бъде равна на произведението на квадрата на страната на тази фигура и числото четири.
• Ако свържете линиите на средата на четирите страни на ромба, получената фигура ще бъде правоъгълник.
• Ако кръгът е вписан в диамант (независимо от неговите ъгли), тогава неговата централна точка ще съвпадне с центъра на пресичане на диагоналите.
• Диагонални диаманти в контакт с осите на симетрията му под ъгъл от деветдесет градуса.
• Тъй като всички страни на ромб са еднакви помежду си по дължина, неговият периметър се изчислява по формулата P = 4 x K (K е дължината на една от страните).

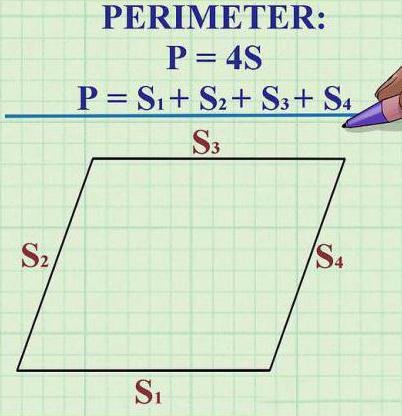
При какви условия е паралелограма с диамант

Както знаете, всеки ромб е успоредник, но не всеки паралелограм е ромб. За да се твърди точно, че представената фигура наистина е ромб, а не обикновен успоредник, тя трябва да отговаря на една от трите основни характеристики, които разграничават ромб. Или и трите наведнъж.

1. Диагоналният паралелограм се пресича под ъгъл от деветдесет градуса.
2. Диагоналите разделят ъглите на две, като действат като техните бисектриси.
3. Не само успоредни, но и съседни страни имат еднаква дължина. Това, между другото, е една от основните разлики между ромба и успоредника, тъй като втората фигура има само паралелни страни, но не и съседни.

При какви условия е ромбовиден квадрат

Според неговите свойства, в някои случаи един ромб може едновременно да се превърне в квадрат. За да потвърдите ясно това твърдение, просто завъртете квадратчето в двете посоки на четиридесет и пет градуса. Получената фигура ще бъде диамант, всеки от които има деветдесет градуса.

Също така, за да потвърдим, че квадратът е ромб, можете да сравните знаците на тези фигури: и в двата случая всички страни са равни, а диагоналите са бисектриси и се пресичат под ъгъл от деветдесет градуса.

Как да намерим областта на ромб, използвайки неговите диагонали

В съвременния свят в интернет можете да намерите почти всички материали за извършване на необходимите изчисления. Така че има маса от ресурси, оборудвани с програми за автоматично изчисляване на площта на определена форма. Освен това, ако (както в случая на ромб) има няколко формули за това, тогава има възможност да се избере кой от тях е най-удобен за използване. Преди всичко обаче е необходимо да може да се изчисли площта на ромб без помощта на компютър и да се ориентира във формули. За един диамант има много, но най-известните от тях са четири.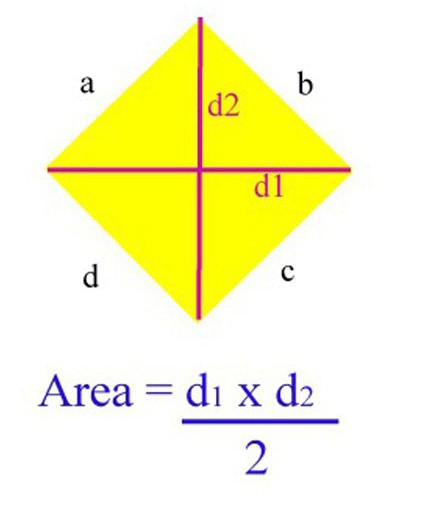

Един от най-лесните и най-често срещаните начини да разберете областта на тази фигура, ако има информация за дължината на диагоналите. Ако проблемът има тези данни, в този случай можете да приложите следната формула, за да намерите областта: S = KM x LN / 2 (KM и LN са диагоналът на ромб KLMN).

На практика можете да проверите валидността на тази формула. Да предположим, че ромбът на KLMN има един диагонал на KM, дължината му е 10 cm, а вторият LN е 8 cm, след което заместваме тези данни в горната формула и получаваме следния резултат: S = 10 x 8/2 = 40 cm ² .

Формула за изчисляване на площта на паралелограма

Има и друга формула. Както бе споменато по-горе в дефиницията на ромб, той не е просто четириъгълник, а също и паралелограма, и има всички характеристики на тази форма. В този случай, за да се намери неговата площ, е разумно да се използва формулата, използвана за успоредника: S = KL x Z. В този случай KL е дължината на страната на успоредника (ромб), а Z е дължината на височината, изтеглена от тази страна.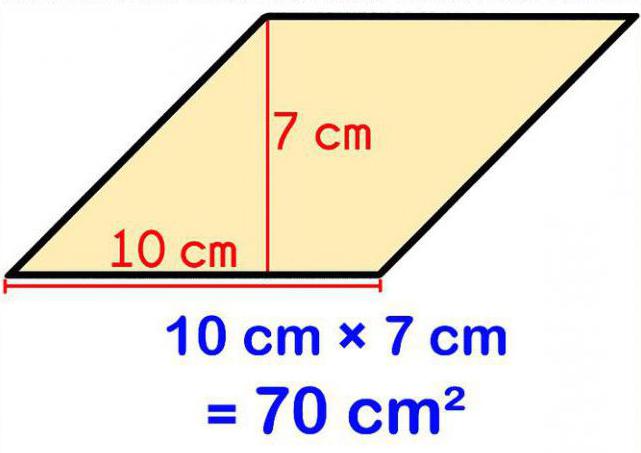

При някои задачи дължината на страната не е дадена, но е известен периметърът на диаманта. Тъй като формулата за намиране е посочена по-горе, тя може да се използва за откриване на дължината на страната. Периметърът на фигурата е 10 см. Дължината на страната може да бъде разпозната чрез обръщане на периметровата формула и разделяне на 10 на 4. Резултатът ще бъде 2,5 см - това е желаната дължина на ромбовата страна.

Сега си струва да се опитаме да заменим това число във формулата, като знаем, че дължината на страната също е 2,5 см. Сега ще се опитаме да поставим тези стойности в споменатата по-горе формула за паралелограма. Оказва се, че площта на ромба е S = 2.5 x 2.5 = 6.25 cm2.

Други начини за изчисляване на диамантената площ

Тези, които вече са усвоили синуси и косинуси, могат да използват формули, които ги съдържат, за да открият областта на ромб. Класическият пример е следната формула: S = KM ² x Sin KLM. В този случай, площта на фигурата е равна на произведението на двете страни на ромба, умножено по синуса на ъгъла между тях. И тъй като в ромбовете всички страни са еднакви, по-лесно е да се произведе една страна в квадрат, както е показано във формулата.

Проверяваме тази схема на практика, а не само на ромб, но на квадрат, който, както е добре известно, има всички ъгли прави, което означава, че са деветдесет градуса. Да предположим, че една от страните е 15 см. Известно е също, че синусът на ъгъл от 90 ° е един. Тогава, по формулата, S = 15 x 15 x Sin 90 ° = 255x1 = 255 cm2 ^.

В допълнение към горното, в някои случаи се използва и друга формула, използваща синуса за определяне на ромбовата площ: S = 4 x R ² / Sin KLM. В този вариант се използва радиусът на кръга, вписан в диаманта. Той се издига до силата на квадрат и се умножава с четири. И целият резултат е разделен от синуса на ъгъла, съседен на вписаната фигура.

Като пример, за простота на изчисленията отново ще вземем квадрата (синусът на ъгъла му винаги ще бъде равен на един). Радиусът на вписаната в него окръжност е 4,4 см. След това площта на ромба ще се изчислява по следния начин: S = 4 x 4,4 ² / Sin 90 ° = 77,44 cm ²

Горните формули за намиране на радиуса на ромб са далеч от единствените по рода си, но те са най-лесни за разбиране и извършване на изчисления.