Метод на крайните елементи и неговото приложение

Методът на крайните елементи се очертава като една от техниките за изучаване на различни дизайни. В момента тя е всеобщо призната като общ начин за решаване на широк спектър от задачи в различни области на технологиите.

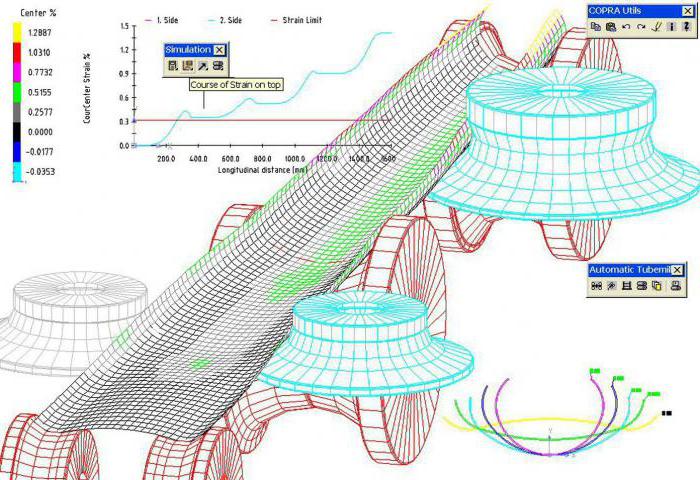
дефиниция

Инженерният анализ чрез метода на крайните елементи се състои в сближаване на непрекъсната среда с безкрайно голям брой степени на свобода чрез набор от елементи (поддомейни), които имат краен брой степени на свобода. Установява се връзка между тези елементи. Разпознаването на метода се обяснява с простотата на нейната математическа форма и физическата интерпретация.

Използва се в механиката

Методът на крайните елементи в механиката на фрактурата и в задачите на структурната механика се изразява като отношението на МКЕ под формата на премествания. Първо, така наречените функции на формата се задават във всеки елемент. Те определят движението във вътрешната област на елемента чрез движение в възлите. Последните са точки, където крайните елементи са комбинирани.

Неизвестни МКЕ са възможни и независими движения на възли на модел с краен елемент (СЕМ). Така KEM дизайнът е система от фиксирани възли. Допълнителните връзки корелират с посоката на възможните движения на възлите.

Същността на метода

В основата си елементарният модел на конструкцията е подобен на основната система на класическия метод на преместване, който се използва при изчисляването на пружинните системи. За да се постигне чувствителната точност на резултатите от изчисленията, използвайки метода на крайните елементи, е необходимо да се намали размерът на елементите, като по този начин се повиши точността на апроксимацията на геометричните характеристики и функциите на изместванията в крайния елемент.

Сложните структури на СЕМ достигат стотици или дори милиони степени на свобода, поради което методът на крайните елементи в машиностроенето е машинно-ориентиран, чието изпълнение е възможно само с помощта на компютри.

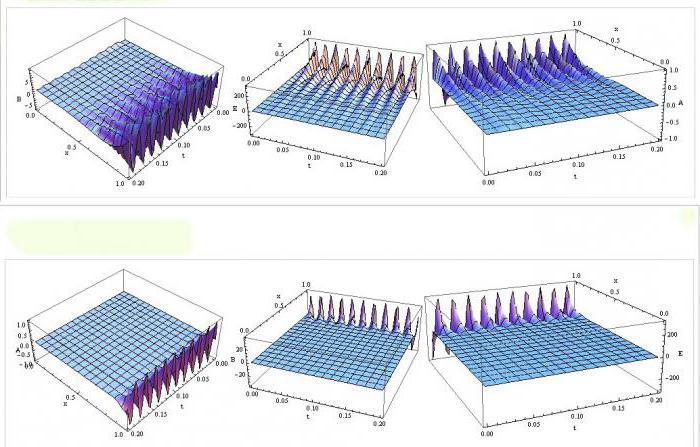
Практическо изпълнение

За да се приложи МКЕ в практиката, е необходимо да се разбере не само теорията на механиката, но и познанията по програмиране. Прилагането на метода на крайните елементи често се основава на вариационните принципи на механиката, които се основават на два основни скалара: потенциал и кинетична енергия еластична конструкция. Дефинирането на тези скалари, независимо от избраната координатна система, позволява да се запише FEM връзката в инвариантна форма.

За улеснение на програмирането съотношенията на МКЕ се записват в компактна матрична или тензорна форма. В момента симулацията по метода на крайните елементи е напълно математически обоснована, създават се високопроизводителни софтуерни продукти, които непрекъснато се усъвършенстват заедно с инструментите за програмиране.

Образователни програми

Техническият прогрес, особено в областта на компютрите, значително промени възгледите за формулиране и решаване на инженерни проблеми. Изграждането на изчислителен модел е тясно свързано с изчислителния процес и е почти невъзможно да се разделят тези два етапа по пътя към получаване на практически резултати.

Методът на крайните елементи е широко използван в инженерната практика, което също допринася за включването му в учебните програми на университетите. МКЕ предвижда начини за изграждане на математически модел на разглежданото явление, основано на неговата физическа същност.

Първите учебници по МКЕ бяха написани на сложен език, но скоро методите на преподаване бяха опростени благодарение на въвеждането на специализирани програми. Например софтуерният пакет Assistant се е доказал добре. Тя ви позволява да тествате знанията на учениците онлайн и допринася за развитието на умения за работа със софтуерни продукти при решаване на практически задачи.

Изчисляване на линейни деформации

Днес основите на метода на крайните елементи се основават на факта, че присъщите на него ценности и понятия не се въвеждат предварително, а произтичат от същността на проблема за структурната механика. Обхватът от проблеми, които могат да бъдат решени с помощта на МКЕ, е почти неограничен. Да вземем за пример задачата за изчисляване на линейната деформация на еластичните структури от действието на статични натоварвания.

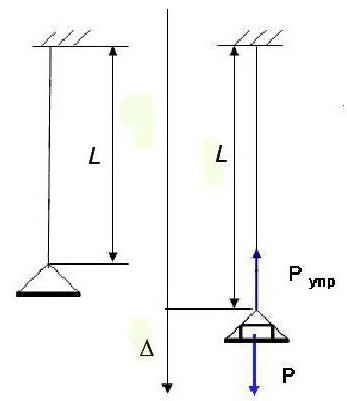
Английският физик Р. Хук е извършил изследване на деформациите на централно натоварени пръчки от различни еластични материали под действието на статична сила: ∆ = Pl / EA.

Той също така установява връзка между количествата, които определят този процес: σ = Eε, където деформацията се изразява чрез отношението ε = ∆ / l, напрежението се обозначава като σ = P / A (тук A е площта на напречното сечение на пръта).

Коефициентът на пропорционалност E определя еластичните характеристики на материала и има физическа същност - напрежението, съответстващо на единично напрежение.

Влияние на статичната сила

Статично действащата сила нараства постепенно с времето (G≥P≥0). Движенията, които генерира, също нарастват постепенно, без ускорение.

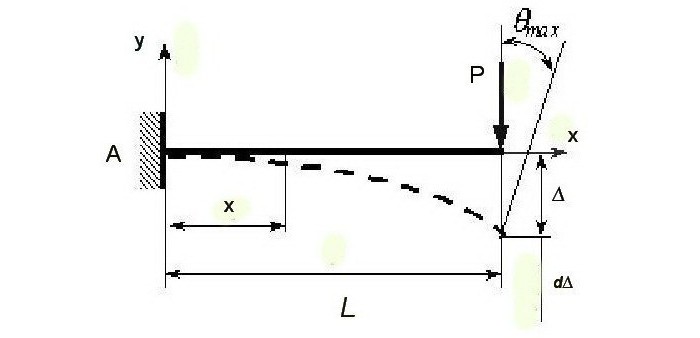
Анализът по метода на крайните елементи позволява да се определи влиянието на статичната сила върху изместването, като се има предвид, че тези индикатори се различават. Увеличение (увеличаване) в сила на безкрайно малка стойност dP съответства на увеличаване (увеличаване) в изместване d∆. Работната сила (P + )P) на изместване d∆ е dA = (P + ∆P) × d∆.

Крайната стойност на работната сила се определя по формулата A = Pd∆.

Нека въведем връзката между размерните променливи под знака на интеграла ∆ = Pα, където α е коефициентът на съответствие, който изразява физическата същност на преместване на точка, към която се добавя единична сила, в посока на тази сила. Съотношението P = Pα определя единицата за измерване α (m / N). От това следва, че d∆ = dPα.

Коефициентът на съответствие съответства на друга важна характеристика на структурата - коефициентът на коравина k = l / α (n / m), който определя силата, която предизвиква единично движение на конструкцията в посока на тази сила.

Като се вземат предвид всички характеристики и коефициенти, крайното уравнение приема: A = PdPα = α × (P 2/2) = (G∆) / 2.

Получава се формулата Clapeyron, която определя действителната работа на статично действаща сила върху изместване, която тя сама генерира в еластично тяло. С помощта на тази техника се изчисляват други числени методи.

Метод на крайните елементи за бар системи

Прътът е пространствено тяло, два размера от което, ширина и височина, са много по-малки от дължината. Това дава възможност да се разглежда нейният физически модел под формата на линия, минаваща през центровете на секциите. Ако външните сили, приложени към пръчката, се намират в една и съща равнина с неговия модел, тогава можем да приемем, че неговите деформации се случват в една и съща равнина.

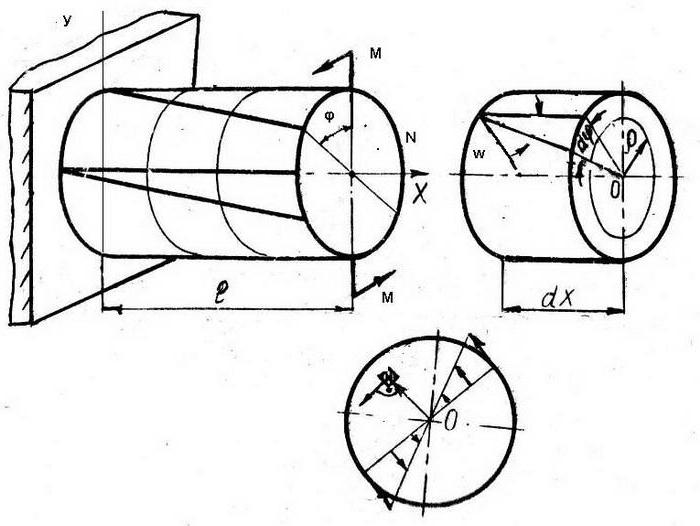
От математическа гледна точка геометричните характеристики на изместване и напрежение в пръта са функции на един и същ аргумент. Отношенията на теорията на еластичността се основават на хипотезата за плоски участъци на пръта. Връзката между деформациите и напреженията съответства на линейния закон на Гук. Във всяка част на пръчката се появяват три равнини на движение:

• u координатата е надлъжната сила;
• координата w - отклонение;
• координата φ - ъгъл на завъртане.

В този случай надлъжното u и деформацията w са независими, а ъгълът на въртене се изразява с формулата d = dw / dx, където dw е размерът на деформация след прилагане на външна сила върху пръта, dx е деформационният сегмент (определен от стойността w + dw).

За безкрайно малък прът dx важи отношението dx = dφ × P.

Потенциална енергия Деформациите на пръти са естествено изчислени в локална координатна система, чиято ос х съвпада с оста на пръта, а оста у е перпендикулярна на оста на пръта: U = ×N × du + ∫M × dφ = ∫1N (du / dx) dx + ½ ×M × (d²w / dx²) dx.

Изопараметричен подход в МКЕ

Разгледайте приложението на метода на крайните елементи в изопараметрична система от крайни елементи на равнинно напрегната структура. Процесът на създаване на крайно-елементен модел на структурите се състои от няколко етапа, първият от които е изграждането на мрежа от крайни елементи (FE), избора на глобална координатна система по отношение на цялата структура и локална система, свързана с крайния елемент.

Най-важната стъпка е да се дефинират функциите на формата, които дават дефиницията на изместванията в рамките на крайния елемент поради движението на нейните възли. Съществуват различни начини за конструиране на функциите на една форма, но те трябва да осигурят изпълнението на няколко условия за апроксимиране на функциите на преместванията.

• Изпълнение на непрекъснатостта на изместванията не само на възлите на крайните елементи, но и на техните граници.
• Осигуряване на консервация на производни на функциите на изместване, свързани с еластичния потенциал.
• Движението на крайния елемент като твърдо цяло число. Това означава, че когато елементът е изместен като твърдо вещество, компонентите на вектора на деформацията са нула.

Проблеми и решения

Теорията на методите на крайните елементи гласи, че FEM отношенията се формират в локалната координатна система. Следователно изброените изисквания за функциите на формата се изпълняват автоматично, ако осите на локалната система са ориентирани по страните на крайния елемент. Такива случаи се случват за крайни елементи на сърцевинни структури, правоъгълни стенни панели и правоъгълни плочи.

На практика обаче съществуват конструкции с контур на произволна дефиниция. В този случай е необходимо да се извърши трансформация, за да се приближат преместванията в глобалната координатна система, което води до прекъсвания на преместванията на границите на крайните елементи и в резултат на загубата на точност на приблизителните изчисления.

Идеята е да се покаже плосък, четириъгълен краен елемент на обща форма на квадрат с локална координатна система, чийто произход е в центъра на тази фигура, и оси, ориентирани по неговите страни. За по-нататъшното използване на крайни елементи във формата на квадрат е необходимо да се установи връзка едно-към-едно между локалните координати на произволно четиристранно FE и локалната координатна система на FE във формата на квадрат. Всъщност, за един квадратен краен елемент, функциите на формата са конструирани по-скоро просто.

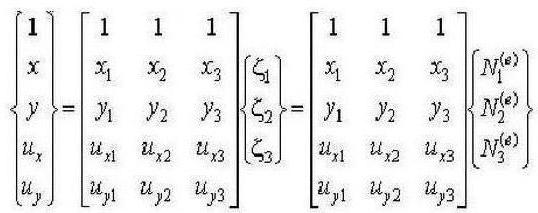
Метод за крайни елементи за изчисления на плочи

Табела е вложка или цилиндрично тяло, чиято височина е много по-малка от размера в плана. Размерът на височината се нарича дебелина на плочата. Равнината, която разделя височината на плочата на половина, се нарича средна или базова равнина. Линията на пресичане на страничната повърхност със средната равнина се нарича контур на плочата.

Счита се, че тънка пластина е тази, за която съотношението на дебелината към по-малкия размер в плана е в рамките на h≤L / 5, където h е дебелината на плочата, L е нейната ширина.

Платката се счита за твърда, ако при действието на напречно натоварване, най-голямата деформация по време на деформацията не надвишава 1/5 от дебелината му.

При изчисляване по метода на FE първо се въвежда координатната система: X ₁ , X ₂ и X ₃ . Началото на осите X ₁ и X ₂ се намира в средната равнина. Оста X3 _е ориентирана по протежение на нормалната към средната равнина.

Изчисленията обикновено се свеждат до изчисляване на изместването (преместването) на дадена плоча в определена точка под въздействието на натоварвания (сили). В произволна точка на плаката, която се счита за триизмерно тяло, се появяват три посоки на движение: U ₁ , U ₂ , U ₃ . Определянето е движението по нормалното към средната равнина, което се нарича деформация и се обозначава с буквата W.

Счита се, че изчисленията се извършват, ако от дадено натоварване (и това обикновено е равномерно разпределено, насочено към повърхността), се установи метод за изчисляване на изместванията U и изместването W в произволна точка на плочата. Отношенията на МКЕ се основават на предложената от физика Кирххофф техническа теория на еластичността.

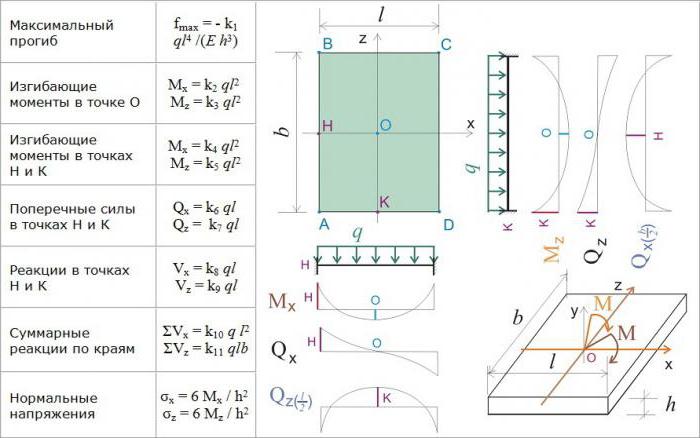
Хипотезите на Кирххоф

Методът на крайните елементи до голяма степен се основава на хипотези, формулирани през 1845 г. от германския физик Г. Kirgofom. Пряката нормална хипотеза гласи, че всяка права линия, нормална към средната равнина на недеформираната плоча, остава права и нормална към средната повърхност на деформираната плоча, а дължината на линията не се променя. Неговата същност е в отсъствието на изместване между слоевете на плочата в дебелина.

Ако осите на декартовите координати са поставени така, че равнините X ₁ , X ₂ съвпадат със средната равнина, от първата част на хипотезата следват следните равенства: y ₁₃ = 0, y ₂₃ = 0. Хипотезата за неизменяемостта на дължината на права линия предполага, че линейната деформация в посоката на оста X ₃ е нула: ε ₃₃ = 0.

Хипотезата за липса на налягане между слоевете на плочата, успоредна на средната повърхност, предполага, че напреженията σ ₃₃ в сравнение с напреженията σ11 и σ22 могат да бъдат пренебрегнати, т.е. σ ₃₃ = 0.

Хипотезата за недеформируемост на средната равнина подсказва, че в средната равнина на плочата няма деформации на напрежението, компресията и срязването. Средната равнина е неутрална. Така в него е изместен U ₁ = U ₂ = 0.

заключение

Методът на крайните елементи, който е широко използван в строителството и механиката, позволява да се изчислят разместванията на различни елементи, подложени на определени натоварвания. Системата, формулирана през 1936 г. от съветските учени, започва да се използва широко десетилетия по-късно, тъй като изисква голямо количество изчисления. С въвеждането на компютри тази задача е опростена.