Екстремни функции. Как да намерим?
Математически анализ - това е доста забавна част от математиката, с която се сблъскват абсолютно всички възпитаници и студенти. Въпреки това не всички обичат Матан. Някои може да не разберат дори елементарни неща като привидно стандартното изследване на дадена функция. Тази статия има за цел да коригира такава грешка. Искате ли да научите повече за анализа на функцията? Искате ли да знаете кои са екстремните точки и как да ги намерите? Тогава тази статия е за вас.
Проучване на графиката на функциите
На първо място, заслужава да се разбере защо е необходимо да се анализира графиката изобщо. Има прости функции за рисуване, което не е трудно. Парабола може да послужи като ярък пример за такава функция. Начертайте графика си не е трудно. Всичко, което е необходимо, е да се намерят числата, за които функцията приема стойност, използвайки проста трансформация и по принцип това е всичко, което е необходимо, за да се начертае графика на парабола.
Но какво, ако функцията, чиято графика трябва да нарисуваме, е много по-трудна? Тъй като свойствата на сложните функции са доста неясни, е необходимо да се извърши цялостен анализ. Само тогава функцията може да бъде изобразена графично. Как да го направя? Отговорът на този въпрос може да се намери в тази статия.
План за анализ на функциите
Първото нещо, което трябва да се направи, е да се проведе повърхностно изследване на функцията, по време на което ще открием областта на дефиницията. Така че нека започнем с ред. Домейнът на дефиницията е колекция от стойностите, с които е зададена функцията. Казано по-просто, това са числата, които могат да се използват във функцията вместо x. За да определите обхвата, просто трябва да погледнете вписването. Например, очевидно е, че функцията y (x) = x 3 + x 2 - x + 43 област на дефиниция е множеството от реални числа. Е, с функция като (x 2 - 2x) / x, всичко е малко по-различно. Тъй като числото в знаменателя не трябва да бъде 0, сферата на функцията ще бъде всички реални числа, в допълнение към нула.
След това трябва да намерите т.нар. Функционални нули. Това са стойностите на аргумента, за който цялата функция приема нулеви стойности. За да направите това, е необходимо функцията да бъде приравнена на нула, да я разгледате подробно и да извършите някои трансформации. Вземете функцията y (x) = (x 2 - 2x) / x, която вече ни е позната. От училищния курс знаем, че частта е 0, когато числителят е нула. Затова изхвърляме знаменателя и започваме да работим с числителя, приравнявайки го на нула. Получаваме x 2 - 2x = 0 и поставяме x за скоби. Следователно x (x - 2) = 0. В резултат на това откриваме, че нашата функция е нула, когато x е 0 или 2.
Екстремни точки на графиката на функциите
По време на изучаването на графиката на функцията мнозина се сблъскват с проблема под формата на точки на екстремум. И това е странно. В крайна сметка, крайностите са доста проста тема. Не вярвате ли? Вижте сами, като прочетете тази част от статията, в която ще говорим за точките на минимума и максимума.
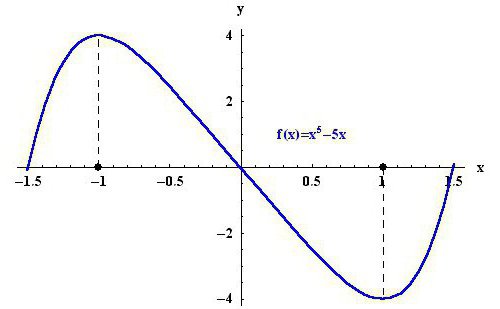
Да започнем е да разберем какво представлява крайност. Екстремът е граничната стойност, която функцията достига на графиката. Оттук се оказва, че има две крайни стойности - максимална и минимална. За по-голяма яснота можете да разгледате снимката по-горе. В изследваната област, точка -1 е максимумът на функцията y (x) = x 5 - 5x, а точка 1 съответно е минималната.
Също така, не бъркайте понятията. Крайните точки на дадена функция са тези аргументи, при които дадена функция приема екстремни стойности. От своя страна екстремумът е стойността на минимумите и максимумите на функцията. Например, разгледайте отново снимката по-горе. -1 и 1 са екстремумите на функцията, а 4 и -4 са самите крайности.
Намиране на екстремни точки
Но как може да се намерят точките на екстремума на дадена функция? Много е просто. Първото нещо, което трябва да направите, е да намерите производната на уравнението. Да предположим, че имаме задачата: "Намерете точките на екстремума на функцията y (x), x е аргументът. За яснота приемаме функцията y (x) = x 3 + 2x 2 + x + 54. Да се диференцира и получи следното уравнение: 3x 2 + 4x + 1. В крайна сметка получихме стандарта квадратично уравнение. Всичко, което трябва да се направи след това, е да го приравним на нула и да намерим корените. Тъй като дискриминантът е по-голям от нула (D = 16 - 12 = 4), това уравнение се определя от два корена. Намерете ги и вземете две стойности: 1/3 и -1. Това ще бъдат точките на екстремума на функцията. Но как се определя кой кой е? Коя точка е максималната и коя е минималната? За да направите това, вземете следващата точка и разберете нейната стойност. Например, вземете числото -2, което е отляво на координатната линия от -1. Заменяме тази стойност в нашето уравнение y (-2) = 12 - 8 + 1 = 5. В резултат на това получаваме положително число. Това означава, че на интервала от 1/3 до -1 функцията се увеличава. Това на свой ред означава, че на интервали от минус безкрайност до 1/3 и от -1 до плюс безкрайност, функцията намалява. По този начин можем да заключим, че числото 1/3 е минималната точка на функцията на изследваната интервал, а -1 е максималната точка.
Сумата от точките на екстремума на функцията

Заслужава да се отбележи, че не само е необходимо да се намерят екстремни точки върху УЕП, но и да се извърши някаква операция с тях (добавяне, умножаване и т.н.). Поради тази причина трябва да се обърне специално внимание на условията на проблема. В крайна сметка, поради невнимание, можете да загубите точки.