Цилиндър. Изгледи, обем на цилиндъра, площ

Името на науката „геометрия“ се превежда като „измерване на земята“. Тя е родена от усилията на първите древни геодезисти. И това беше така: по време на наводненията на свещения Нил водните потоци понякога отмиваха границите на земеделските райони и новите граници не можеха да съвпаднат със старите. Данъците на селяните се изплащаха в хазната на фараона пропорционално на размера на земята. Измерването на площта на обработваемата земя в новите граници след разлива включваше специални хора. В резултат на тяхната дейност се появява нова наука, която се развива в древна Гърция. Там тя получи името и придоби почти съвременен вид. По-късно терминът стана международното име на науката за плоски и триизмерни фигури.

Планиметрията е част от геометрията, която изучава плоски фигури. Друг раздел на науката е стереометрията, която разглежда свойствата на пространствените (триизмерни) фигури. Тези цифри включват цилиндъра, описан в тази статия.

Примери за наличие на цилиндрични обекти в ежедневието са изобилстващи. Почти всички детайли на въртене - валове, втулки, шийки, оси и др. - имат цилиндрична (много по-малко конична) форма. Цилиндърът е широко използван в строителството: кули, поддържащи, декоративни колони. А освен ястията, някои видове опаковки тръби с различни диаметри. И накрая - известните шапки, които отдавна са се превърнали в символ на мъжката елегантност. Списъкът е безкраен.

Определение на цилиндър като геометрична фигура

Цилиндърът (кръговият цилиндър) се нарича фигура, състояща се от два кръга, които при желание се комбинират с помощта на паралелен трансфер. Тези кръгове са основите на цилиндъра. Но линиите (правите), свързващи съответните точки, се наричат ​​„генератори“.

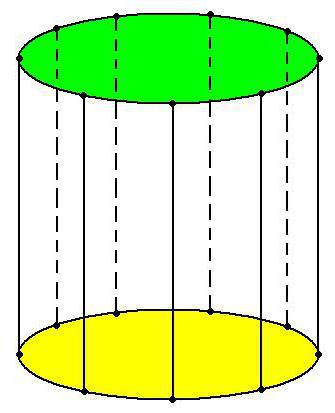
Важно е базите на цилиндъра да са винаги равни (ако това условие не е изпълнено, тогава пред нас е пресечен конус, нещо друго, но не и цилиндър) и са в паралелни равнини. Сегментите, свързващи съответните точки на кръговете, са успоредни и равни.

Комбинацията от безкраен набор от генератори е нищо друго освен страничната повърхност на цилиндъра - един от елементите на това геометрична форма. Друг важен компонент са дискутираните по-горе кръгове. Те се наричат ​​бази.

Видове цилиндри

Най-простият и най-често срещан тип цилиндър е кръгъл. Тя се формира от две редовни кръгове, които действат като бази. Но вместо това може да има други цифри.

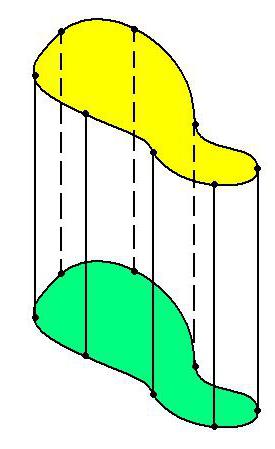
Основите на цилиндрите могат да образуват (освен кръгове) елипси, други затворени фигури. Но цилиндърът не е задължително да има затворена форма. Например, парабола, хипербола, друга отворена функция може да служи като основа на цилиндър. Такъв цилиндър ще бъде отворен или разгърнат.

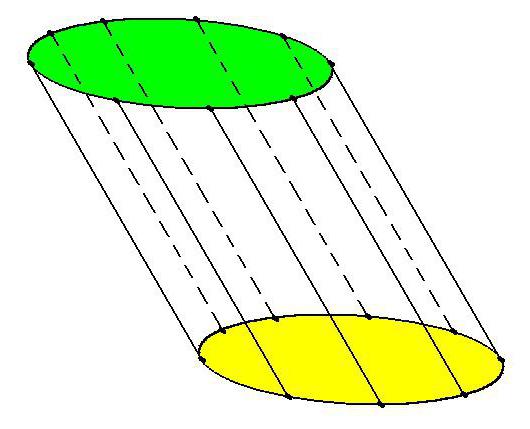
Ъгълът на наклона, формиращ основите на цилиндрите, може да бъде прав или наклонен. Правият цилиндър е строго перпендикулярно на равнината на основата. Ако този ъгъл е различен от 90 °, цилиндърът е наклонен.

Какво е повърхността на въртене

Прав кръгъл цилиндър, без съмнение - най-често използваната повърхност на въртене в машиностроенето. Понякога, по технически причини, се използват конични, сферични, някои други видове повърхности, но 99% от всички въртящи се шахти, оси и др. направени точно под формата на цилиндри. За да разберем по-добре какво е повърхността на революцията, можем да разгледаме как се формира самият цилиндър.

Да предположим, че има някаква права линия, разположена вертикално. ABCD е правоъгълник, една от страните на която (сегмент AB) лежи върху линията a . Ако завъртите правоъгълника около права линия, както е показано на фигурата, обемът, който той заема, се върти, ще бъде нашето въртящо тяло - прав кръгов цилиндър с височина H = AB = DC и радиус R = AD = BC.

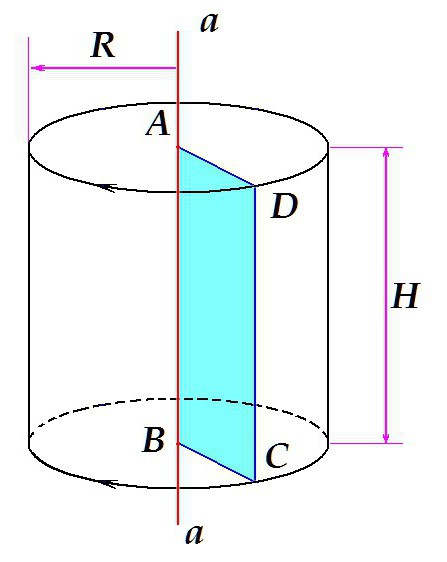
В този случай в резултат на въртенето на фигурата се получава правоъгълник - цилиндър. Въртене на триъгълник, можете да получите конус, завъртане на полукръг - топка и т.н.

Площ на цилиндъра

За да се изчисли повърхностната площ на правилния правоъгълен цилиндър, е необходимо да се изчисли площта на основите и страничната повърхност.

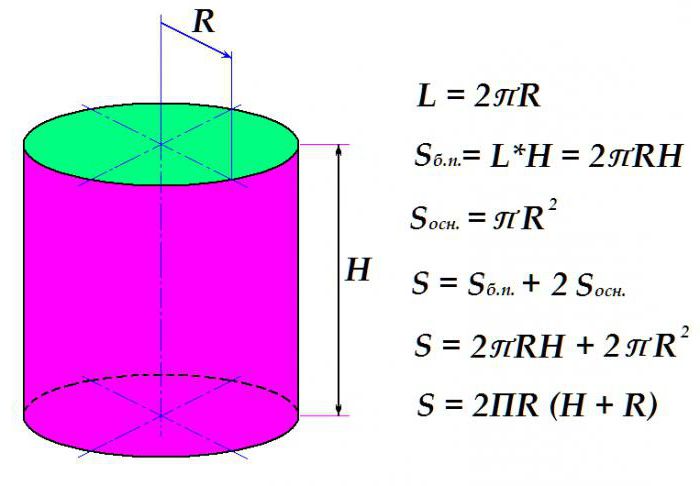
Първо, помислете как да изчислите площта на страничната повърхност. Това е произведението на обиколката на цилиндъра по височината на цилиндъра. Обиколката, на свой ред, той е равен на два пъти произведението на универсалното число Р и радиуса на окръжността.

Площта на окръжността, както е известно, е равна на произведението на P по квадрата на радиуса. Така, чрез добавяне на формулите за зоната на определяне на страничната повърхност с двойно изразяване на базовата област (има две от тях) и произвеждащи прости алгебрични преобразувания, получаваме крайния израз за определяне на площта на цилиндъра.

Определяне на размера на фигурата

Обемът на цилиндъра се определя по стандартната схема: площта на основата се умножава по височината.

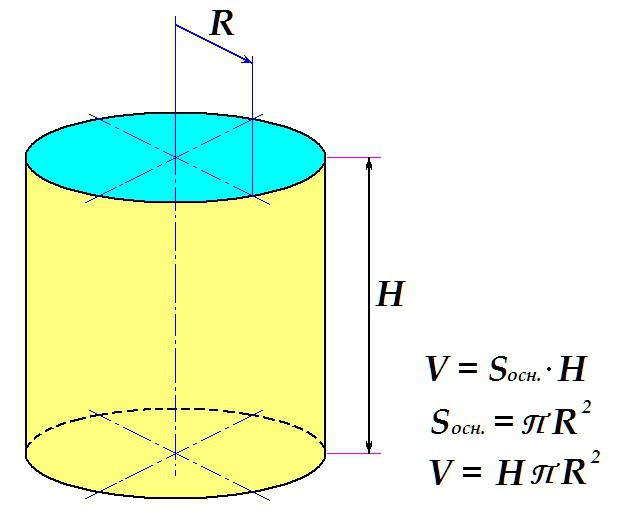
Така крайната формула е следната: желаното се определя като произведение на височината на тялото от универсалния номер Р и квадрата на основния радиус.

Получената формула, трябва да кажа, е приложима за решаване на най-неочакваните проблеми. По същия начин, както обемът на цилиндъра, например, се определя обемът на електрическите проводници. Това е необходимо, за да се изчисли масата на жиците.

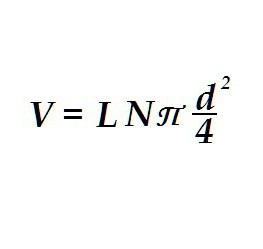
Разликата във формулата е само, че вместо радиуса на един цилиндър има диаметър на проводника, разделен на две, а броят на живите в проводника N се появява в израза. Освен това се използва дължината на проводника вместо височината. Така обемът на "цилиндъра" се изчислява не от един, а от броя на жиците в плитката.

Такива изчисления често се изискват на практика. Всъщност, значителна част от водния резервоар е направена във формата на тръба. И за изчисляване на обема на цилиндъра често е необходимо дори в домакинството.

Обаче, както вече беше споменато, формата на цилиндъра може да бъде различна. И в някои случаи е необходимо да се изчисли кое е обемът на наклонения цилиндър.

Разликата е, че площта на основата се умножава не по дължината на генератора, както в случая на прав цилиндър, а с разстоянието между равнините - перпендикулярния сегмент, който е изграден между тях.

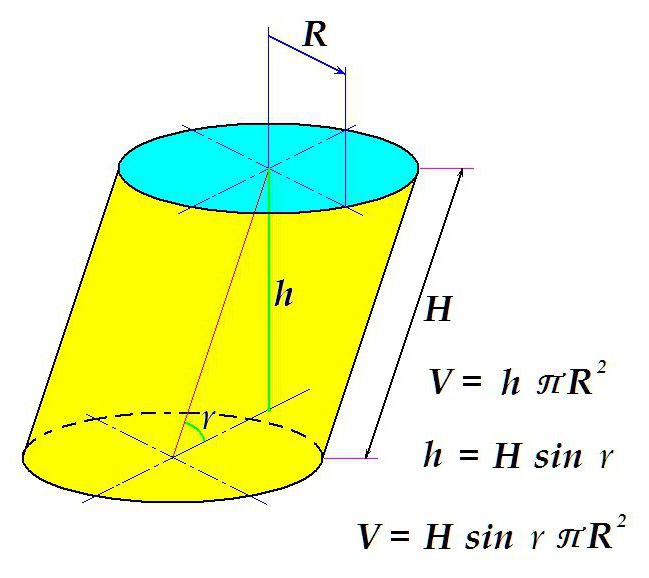
Както може да се види от фигурата, такъв сегмент е равен на произведението на дължината на образуващата и синуса на ъгъла на наклона на образуващата към равнината.

Как да се изгради цилиндричен размах

В някои случаи е необходимо да се издълбават цилиндрични рамена. На следващата фигура са показани правилата, чрез които е направен заготовка за производството на цилиндър с определена височина и диаметър.

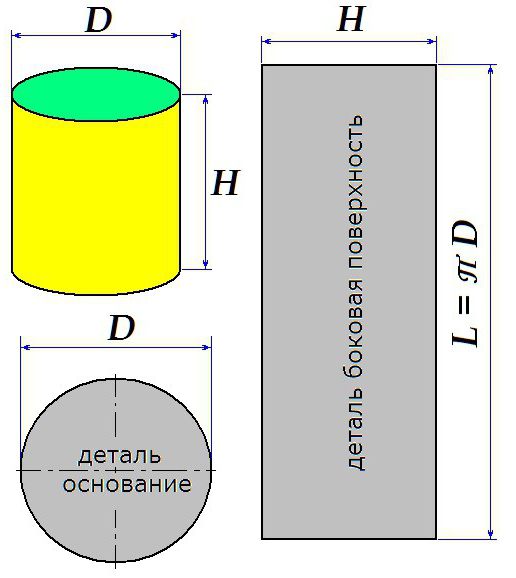
Обърнете внимание, че фигурата е показана без оглед на шевовете.

Разлики в коничния цилиндър

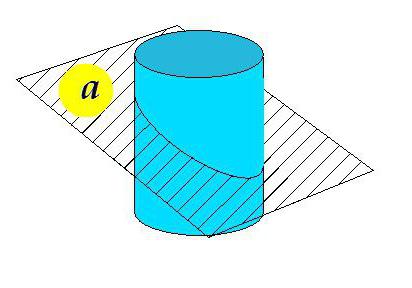
Представете си някакъв прав цилиндър, ограничен от едната страна от равнина, перпендикулярна на генераторите. Но равнината, ограничаваща цилиндъра, от друга страна, не е перпендикулярна на генераторите и не е паралелна на първата равнина.

Фигурата показва наклонен цилиндър. Равнината и под определен ъгъл, различен от 90 ° към генераторите, пресича фигурата.

Такава геометрична форма е по-често срещана в практиката под формата на тръбни съединения (колена). Но има дори сгради, построени под формата на наклонен цилиндър.

Геометрични характеристики на скосения цилиндър

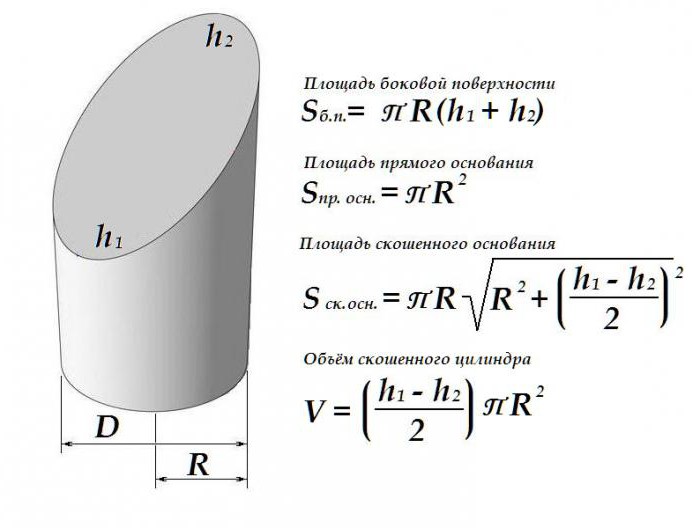
Наклонът на една от плоскостите на наклонения цилиндър леко променя реда на изчисляване както на повърхността на такава фигура, така и на нейния обем.