Центростремително ускорение - изходна формула и практическо приложение

Centripetal ускорение ни придружава навсякъде. Това прави нашето Земята се върти около слънцето. Получената гравитация ни позволява да съществуваме на тази планета. Как може да се разбере какво е центростремителното ускорение? Определението на тази физическа величина е представено по-долу.

наблюдения

Най-простият пример за ускоряване на движение на тялото в кръг може да се наблюдава чрез завъртане на камък на въже. Издърпваш въжето и въжето дърпа камъка към центъра. Във всеки момент въжето казва на камъка определено количество движение, и всеки път - в нова посока. Можете да си представите движението на въжето под формата на поредица от слаби тласъци. Идиот - въжето променя посоката си, друг ритник - друга промяна, и така нататък в кръг. Ако внезапно освободите въжето, пристъпът ще спре и заедно с тях ще спре промяната в посоката на скоростта. Камъкът ще се движи по посока на допирателната към кръга. Възниква въпросът: "С какво ускорение ще се движи тялото в този момент?"

Формула за центростремително ускорение

На първо място, заслужава да се отбележи, че движението на тялото в кръг е трудно. Един камък участва в два вида движения едновременно: под действието на сила той се движи към центъра на въртене, а в същото време тангенциално към кръга, той се отдалечава от този център. Според Втория закон на Нютон силата, която държи камъка върху въжето, е насочена към центъра на въртене по това въже. Също така ще бъде насочено към вектора на ускорението.

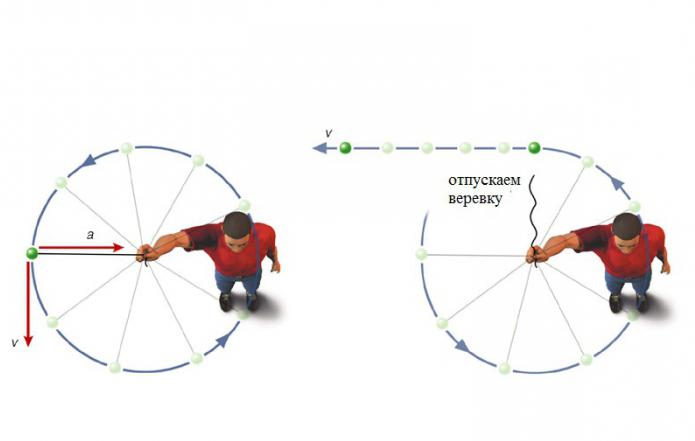
Нека за известно време t нашият камък, движещ се равномерно със скорост V, достигне от точка А до точка Б. Да предположим, че в момента, когато тялото пресече точка В, центростремителната сила е престанала да действа върху нея. Тогава за определен период от време тя ще падне в точката К. Тя лежи върху допирателната. Ако в същия момент от времето на тялото действат само центростремителни сили, тогава по време t, движейки се със същото ускорение, то ще се появи в точката О, която е разположена на права линия, която представлява диаметъра на кръга. И двата сегмента са вектори и се подчиняват на правилото за добавяне на вектор. В резултат на сумирането на тези две движения в интервала от време t получаваме полученото движение по дъгата AB.

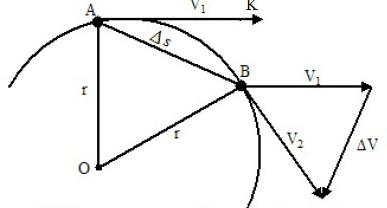
Ако интервалът от време t се приеме за незначителен, тогава дъгата AB ще се различава малко от хордата AB. По този начин е възможно да се замени движението по дъга чрез движение по хорда. В този случай движението на камъка по хордата ще се подчинява на законите на движението по права линия, т.е. изминатото разстояние AB ще бъде равно на произведението на скоростта на камъка по време на неговото движение. AB = V x t.

Означете желаното центростремително ускорение с буквата а. Тогава пътеката, покрита само от действието на центростремителното ускорение, може да бъде изчислена с помощта на формулата с равномерно ускорено движение:

AO = при 2/2.

Разстоянието AB е равно на произведението на скоростта и времето, т.е. AB = V x t,

AO - предварително изчислена по формулата равномерно ускорено движение за придвижване по права линия: AO = при 2/2.

Подменяйки тези данни във формула и я трансформираме, получаваме проста и елегантна центростремителна ускорителна формула:

a = v ² / R

Това може да бъде изразено по следния начин: центростремителното ускорение на тялото, движещо се в кръг, е равно на частното от разделянето на линейната скорост на квадрата от радиуса на кръга, в който тялото се върти. Центростремителната сила в този случай ще изглежда като изображението по-долу.

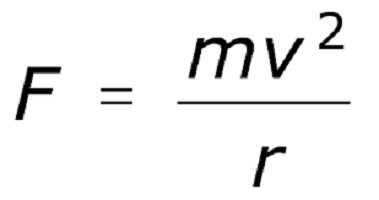
Ъглова скорост

Ъглова скорост равно на частното на линейната скорост, разделена на радиуса на окръжността. Обратното също е вярно: V = ωR, където ω е ъгловата скорост

Ако замените тази стойност във формулата, можете да получите израз на центробежно ускорение за ъгловата скорост. Тя ще изглежда така:

a = ω ² R.

Ускорение без промяна на скоростта

И все пак, защо едно тяло с ускорение, насочено към центъра, не се движи по-бързо и не се приближава към центъра на въртене? Отговорът се крие в самата формулировка на ускорението. Фактите сочат, че шофирането в кръг е реално, но за да се поддържа това, се изисква ускорение, насочено към центъра. Под действието на сила, причинена от това ускорение, настъпва промяна в количеството на движението, в резултат на което траекторията на движение непрекъснато се огъва, променяйки посоката на вектора на скоростта през цялото време, но без да променя своята абсолютна стойност. Движейки се в кръг, нашият многострадален камък се втурва навътре, иначе ще продължи да се движи по допирателна. Всеки миг от време, оставяйки допирателна, камъкът се привлича към центъра, но не попада в него. Друг пример за центростремително ускорение може да бъде водната скиорка, описваща малките кръгове на водата. Фигурата на спортиста е наклонена; той сякаш пада, продължава да се движи и се накланя напред.

Така можем да заключим, че ускорението не увеличава скоростта на тялото, тъй като векторите на скоростта и ускорението са перпендикулярни един на друг. Добавяйки към вектора на скоростта, ускорението само променя посоката на движение и поддържа тялото в орбита.

Превишение на границата на безопасност

В предишния опит се справихме с идеалното въже, което не беше разкъсано. Но, да речем, нашето въже е най-често срещаното и дори можете да изчислите силата, след което тя просто ще се счупи. За да се изчисли тази сила, е достатъчно да се сравни границата на безопасност на въжето с товара, който изпитва в процеса на въртене на камъка. Като въртите камъка с по-бърза скорост, вие му придавате повече движение, което означава повече ускорение.

При диаметър на ютско въже от около 20 mm неговата якост на опън е около 26 kN. Трябва да се отбележи, че дължината на въжето не се появява никъде. Чрез въртене на товар с размер 1 kg на въже с радиус 1 m, може да се изчисли, че линейната скорост, необходима за счупване, е 26 x 10 ³ = 1 kg x V 2/1 m. Така скоростта, която е опасна да надвиши, е равна на 26 х 10 ³ = 161 m / s.

притегляне

При разглеждането на опита пренебрегнахме действието на силата на гравитацията, тъй като при такива високи скорости влиянието му е незначително. Но можете да видите, че когато размотавате дълъг въже, тялото описва по-сложна траектория и постепенно се приближава към земята.

Небесни тела

Ако прехвърлим законите на движение по кръг в пространството и ги приложим към движение небесни тела Можете да отворите няколко отдавна познати формули. Например, силата, с която тялото е привлечено от Земята, е позната по формулата:

F = m * g.

В нашия случай факторът g е много центростремителното ускорение, което е извлечено от предишната формула. Само в този случай ролята на камъка ще се изпълнява от небесното тяло, привлечено от Земята, и ролята на въжето - силата на гравитацията. Умножителят g ще бъде изразен чрез радиуса на нашата планета и скоростта на нейното въртене.

резултати

Същността на центростремителното ускорение се състои в трудната и неблагодарна работа за поддържане на движещо се тяло в орбита. Има парадоксален случай, когато с постоянно ускорение, тялото не променя величината на своята скорост. За нетренирания ум такова твърдение е доста парадоксално. Въпреки това при изчисляване на движението на електрона около ядрото и при изчисляване на скоростта на въртене на звезда около черна дупка, центростремителното ускорение не играе последната роля.