Какви трудности очакват онези, които са поели ангажимент за добавяне на корени?

Темата за квадратните корени е задължителна в учебната програма на курса по математика. Без тях да не се прави при вземането на решение квадратни уравнения. И по-късно става необходимо не само да се извлекат корените, но и да се извършат други действия с тях. Сред тях са доста сложни: степенуване умножение и разделяне. Но има доста прости: изваждане и добавяне на корени. Между другото, те изглеждат само на пръв поглед. Изпълнението им без грешки не винаги е лесно за някой, който току-що започва да се запознава с тях.

Какво е коренът на математиката?

Това действие възниква в противовес на експоненцирането. Математиката предполага съществуването на две противоположни операции. Има изваждане за добавяне. Умножението се противопоставя на разделянето. Обратното на степента е извличането на съответния корен.

Ако има две в силата, тогава коренът ще бъде квадрат. Най-често се среща в училищната математика. Той дори няма индикация, че той е квадратен, т.е. номер 2 не му се приписва, а математическата нотация на този оператор (радикал) е показана на фигурата.

От описаното действие гладко следва неговото определение. За извличане квадратен корен от определен брой, трябва да разберете кой ще даде, когато се умножи в себе си, радикалния израз. Този номер ще бъде квадратният корен. Ако го напишете математически, получавате следното: x * x = x ² = y, след това =u = x.

Какво можете да направите с тях?

В основата си коренът е частична степен, в която има единица в числителя. А знаменателят може да бъде всеки. Например, в квадратния корен, той е равен на два. Следователно всички действия, които могат да бъдат извършени с градуси, ще бъдат валидни за корените.

И изискванията за тези действия са еднакви. Ако умножението, делението и експоненцирането не срещнат трудности за учениците, добавянето на корени, както и тяхното изваждане, понякога води до объркване. И всичко това, защото искам да извърша тези операции без оглед на коренния знак. И тук грешките започват.

Какви са правилата за добавянето и изваждането им?

Първо трябва да запомните две категорични "не":

• не добавяйте и не изваждайте корените като прости числа не е възможно да се напишат еднозначни обобщени радикални изрази и да се извършват математически операции с тях;
• не можете да добавяте и изваждате корени с различни индикатори, като квадратен и кубичен.

Добър пример за първата забрана: +6 + ≠10 ≠ √16, но √ (6 + 10) = .16 .

Във втория случай е по-добре да се ограничим до опростяване на корените. И в отговора да се остави тяхната сума.

Сега към правилата

1. Намерете и групирайте подобни корени. Това означава, че тези, които имат не само еднакви числа под радикала, но и самите те имат един и същ показател.
2. За да извършите добавянето на корените, обединени в една група от първото действие. Тя е лесна за изпълнение, защото просто трябва да добавите стойностите, които стоят пред радикалите.
3. Корените се извличат в тези термини, в които радикалният израз формира цял квадрат. С други думи, не оставяйте нищо под знака на радикала.
4. Опростете израза. За да направите това, трябва да ги разложите в прости фактори и да видите дали те няма да дадат квадрат от произволно число. Ясно е, че това е вярно, когато става въпрос за квадратен корен. Когато експонентът е три или четири, тогава основните коефициенти трябва да дадат куб или четвърта сила на число.
5. Отстранете от множителя радикален знак, който дава цялата степен.
6. Вижте дали подобни термини се появяват отново. Ако е така, изпълнете отново второто действие.

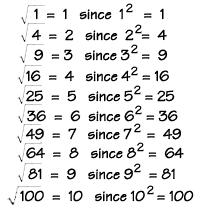
В ситуация, в която задачата не изисква точната стойност на корена, тя може да бъде изчислена на калкулатора. Безкраен десетичен дроб, който ще се показва в прозореца му, кръг. Най-често се прави на стотен. След това изпълнявайте всички операции десетични дроби.

Препоръка: след разлагане на основни фактори, трябва да проверите. Това означава, че ги умножете един върху друг и проверете дали е получена първоначалната стойност.

Това е цялата информация за това как се извършва добавянето на корените. Примерите по-долу ще илюстрират горното.

Първа задача

Изчислете стойността на изразите:

а) +2 + 3√32 + ½ 8128 - 6√18;

б) --75 - 7147 + --48 - 1/5 ;300;

в) 75275 - 10√11 + 2'99 + 6396.

Решението.

а) Ако следвате горния алгоритъм, е ясно, че за първите две действия в този пример няма нищо. Но можете да опростите някои радикални изрази.

Например, 32 се разлага на два фактора 2 и 16; 18 ще бъде равен на произведението от 9 и 2; 128 е 2 с 64. Като се има предвид това, изразът ще бъде написан по следния начин:

+2 + 3√ (2 * 16) + ½ √ (2 * 64) - 6 √ (2 * 9).

Сега трябва да премахнем от радикалния знак онези фактори, които дават квадрата на числото. Това е 16 = 4 ² , 9 = 3 ² , 64 = 8 ² . Изразът ще изглежда така:

+2 + 3 * 4√2 + ½ * 8 --2 - 6 * 3√2.

Нуждаете се от малко по-лесно писане. За да направите това, умножете коефициентите пред коренните знаци:

+2 + 12√2 + 4 --2 - 12√2.

В този израз всичките термини се оказаха сходни. Затова те просто трябва да се сгънат. Отговорът ще бъде: 5√2.

б) Подобно на предишния пример, добавянето на корените започва с тяхното опростяване. Радикалните изрази 75, 147, 48 и 300 ще бъдат представени от следните двойки: 5 и 25, 3 и 49, 3 и 16, 3 и 100. Всеки от тях има число, което може да бъде премахнато от коренния знак:

5√5 - 7√3 + 4√3 - 1/5 * 10√3.

След опростяване получаваме отговор: 5√5 - 5√3. Тя може да бъде оставена в тази форма, но е по-добре да се извади общия фактор 5 за скобата: 5 (--5 - )3).

в) И отново, факторинг: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36. След премахване на факторите от коренния знак, получаваме:

5√11 - 10√11 + 2 * 3√11 + 6√11. След въвеждането на такива условия получаваме резултат: 7√11.

Пример с частични изрази

√ (45/4) - --20 - 5√ (1/18) - 1/6 45245 + √ (49/2).

Факторите ще трябва да разлагат следните числа: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Подобно на вече разгледаните, трябва да премахнете факторите от коренния знак и да опростите израза:

3/2 --5 - 2√5 - 5/3 √ (½) - 7/6 +5 + 7 (½) = (3/2 - 2 - 7/6) --5 - (5/3 - 7 ) √ (½) = - 5/3 +5 + 16/3 √ (½).

Този израз изисква да се отървем от ирационалността в знаменателя. За да направите това, умножете по /2 / √2 втория термин:

- 5/3 +5 + 16/3 √ (½) * /2 / =2 = - 5/3 +5 + 8/3 .2.

За пълнота на действието е необходимо да се избере част от факторите преди корените. В първия, той е равен на 1, във втория - 2.