Проекцията на точката в равнината. Проекция на точка на права линия върху равнина
Изучаването на свойствата на фигурите в пространството и на равнината е невъзможно без познаване на разстоянията между точка и такива геометрични обекти като права и равнина. В тази статия ще покажем как да намерим тези разстояния, като вземем предвид проекцията на точка върху равнина и по права линия.
Уравнение на линия за двумерни и триизмерни пространства
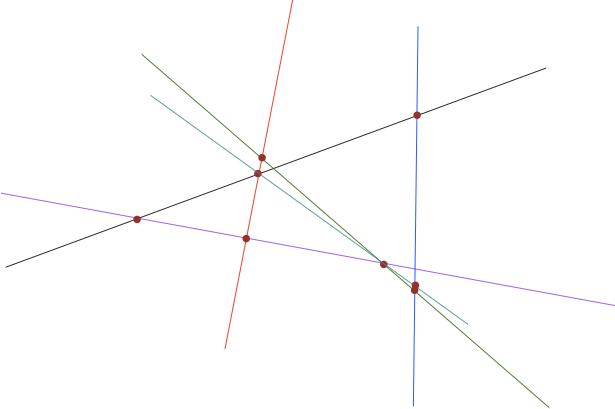
Изчисляването на разстояния на точка до права и равнина се извършва с помощта на неговата проекция върху тези обекти. За да можем да намерим тези проекции, трябва да знаем в каква форма са дадени уравненията за правите и равнините. Да започнем с първото.
Права линия е съвкупност от точки, всяка от които може да бъде получена от предишната чрез прехвърляне към паралелни вектори. Например, има точка M и N. Векторът MN them, който ги свързва, отнема M към N. Има и трета точка P. Ако векторът MP¯ или NP¯ е успореден на MN¯, то всичките три точки на една линия лежат и образуват.
В зависимост от размера на пространството уравнението, определящо линията, може да промени формата си. По този начин добре познатата линейна зависимост на y координатата на x в пространството описва равнина, която е успоредна на третата z ос. В тази връзка в тази статия ще разгледаме само векторното уравнение за линията. Той има същия вид за равнината и триизмерното пространство.
В пространството права линия може да бъде дефинирана със следния израз:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (a; b; c)
Тук координатните стойности с нулеви индекси съответстват на права линия, принадлежаща на определена точка, u¯ (a; b; c) е координатите на насочващия вектор, който лежи на дадена права линия, α е произволно реално число, което може да се промени, като се получат всички точки на права линия. Това уравнение се нарича вектор.
Често горното уравнение е написано в отворена форма:
х = х 0 + а * а;
y = y 0 + α * b;
z = z 0 + α * c
По подобен начин можем да напишем уравнението за права линия в равнината, т.е. в двуизмерното пространство:
(x; y) = (x 0 ; y 0 ) + α * (a; b);
х = х 0 + а * а;
y = y 0 + α * b
Равнинно уравнение
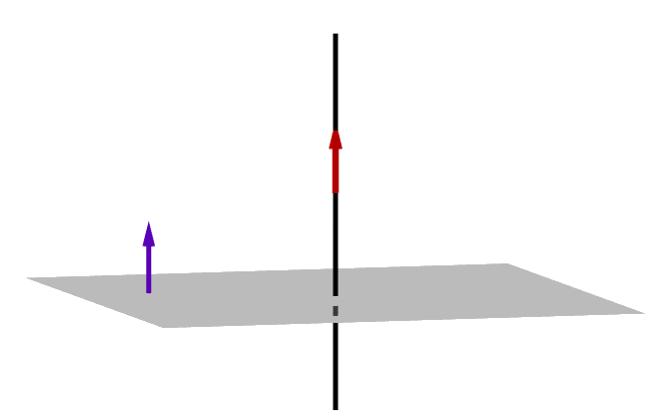
За да можете да намерите разстоянието от една точка до равнината на проекциите, трябва да знаете как се определя равнината. Както и права линия, тя може да бъде представена по няколко начина. Тук разглеждаме само едно: общото уравнение.
Да предположим, че точката M (x 0 ; y 0 ; z 0 ) принадлежи на равнината, а векторът n ¯ (A; B; C) е перпендикулярно на него, след това за всички точки (x; y; z) на равнината следващото равенство ще бъде вярно:
A * x + B * y + C * z + D = 0, където D = -1 * (A * x 0 + B * y 0 + C * z 0 )
Трябва да се помни, че в това общо уравнение на равнината, коефициентите А, В и С са координатите на нормата към равнината на вектора.
Изчисляване на разстояния по координати
Преди да пристъпим към разглеждане на проекциите в равнината на точка и по права линия, трябва да се припомни как трябва да се изчисли разстоянието между две известни точки.
Да предположим, че има две пространствени точки:
A 1 (x 1 ; y 1 ; z 1 ) и A 2 (x 2 ; y 2 ; z 2 )
Тогава разстоянието между тях се изчислява по формулата:
A 1 A 2 = √ (((x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 + (z 2 -z 1 ) 2 )
Чрез този израз се определя и дължината на вектора A 1 A 2 ¯.
За случая на равнина, когато са дадени две точки само с чифт координати, можете да напишете подобно уравнение без присъствието на член с z в него:
A 1 A 2 = √ (((x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 )
Сега ще разгледаме различни случаи на проекция на равнина на точка на права линия и на равнина в пространството.
Точка, линия и разстояние между тях
Да предположим, че има някаква точка и права линия:
Р2 (х 1 ; у 1 );
(x; y) = (x 0 ; y 0 ) + α * (a; b)
Разстоянието между тези геометрични обекти ще съответства на дължината на вектора, началото на което се намира в точката P 2 , а краят е в такава точка P на посочената права линия, за която векторът P 2 P ¯ на тази права е перпендикулярна. Точката Р се нарича проекция на точка Р 2 върху въпросната линия.
На фигурата по-долу е показана точката P 2 , разстоянието d до правата линия, както и векторът на посоката v 1 ¯. Също така на линията е избрана произволна точка Р 1 и от нея се изтегля вектор до Р 2 . Точката P тук съвпада с мястото, където перпендикулярът пресича линията.
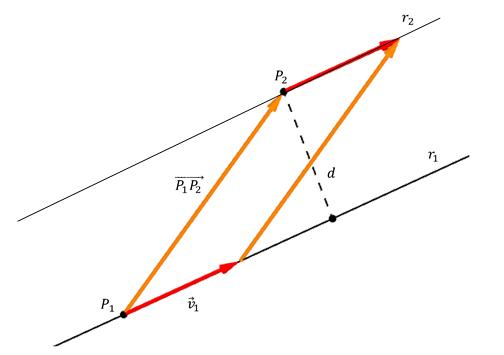
Вижда се, че оранжевите и червените стрелки образуват успоредник, чиито страни са векторът P 1 P 2 ¯ и v 1 ¯, а височината е d. От геометрията е известно, че за да се намери височината на успоредника, неговата площ трябва да бъде разделена на дължината на основата, върху която е спуснат перпендикуляра. Тъй като площта на успоредника се изчислява като векторно произведение на неговите страни, получаваме формулата за изчисляване на d:
d = | [P 1 P 2 ¯ * v 1 ¯] | / | v 1 ¯ |
Всички вектори и координати на точки в този израз са известни, така че можете да го използвате, без да извършвате никакви трансформации.
Би било възможно този проблем да се реши по различен начин. За да направите това, запишете две уравнения:
- скаларният продукт P 2 P ¯ на v 1 ¯ трябва да бъде равен на нула, тъй като тези вектори са взаимно перпендикулярни;
- координатите на точката P трябва да отговарят на уравнението на линия.
Тези уравнения са достатъчни, за да се намерят координатите на Р, а след това и дължината d по формулата, дадена в предишния параграф.
Задачата да се намери разстоянието между линията и точката
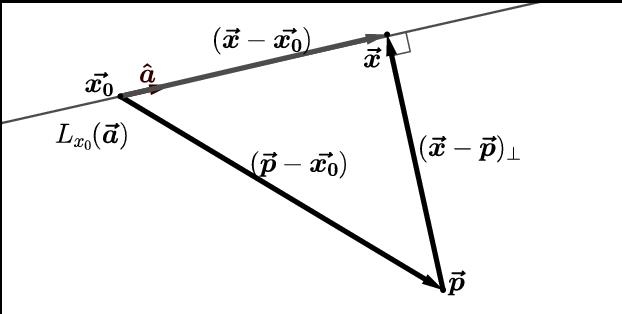
Ние показваме как да използваме тази теоретична информация за решаване на конкретен проблем. Да предположим, че следната точка и ред са известни:
М (5; -3);
(x; y) = (3; 1) - α * (0; 2)
Необходимо е да се намерят точките на проекция върху права линия в равнината, както и разстоянието от М до права линия.
Означаваме проекцията, която се намира от точката M 1 (x 1 ; y 1 ). Ние решаваме този проблем по два начина, описани в предходния параграф.
Метод 1. Векторът на посоката v 1 ¯ има координати (0; 2). За да изградите успоредник, изберете точка, принадлежаща на права линия. Например точка с координати (3; 1). Тогава векторът от втората страна на успоредника ще има координати:
(5; -3) - (3; 1) = (2; -4)
Сега е необходимо да се изчисли произведението на векторите, определящи страните на успоредника:
[(2; -4) * (0; 2)] = 4
Заменяме тази стойност във формулата, получаваме разстоянието d от M до права линия:
d = 4 / =4 = 2
Метод 2. Сега ще намерим по друг начин не само разстоянието, но и координатите на проекцията М на линията, както се изисква от състоянието на проблема. Както бе споменато по-горе, за решаване на проблема е необходимо да се създаде система от уравнения. Тя ще изглежда така:
(x 1 -5) * 0 + (y 1 +3) * 2 = 0;
(x 1 ; y 1 ) = (3; 1) -α * (0; 2)
Решаваме тази система:
у 1 = -3;
x 1 = 3
Проекцията на началната точка на координатата е M 1 (3; -3). Тогава изискваното разстояние е:
d = | MM 1 ¯ | = √ (4 + 0) = 2
Както можете да видите, и двете решения дават същия резултат, който показва коректността на изпълнените математически операции.
Проекция на точка на равнина
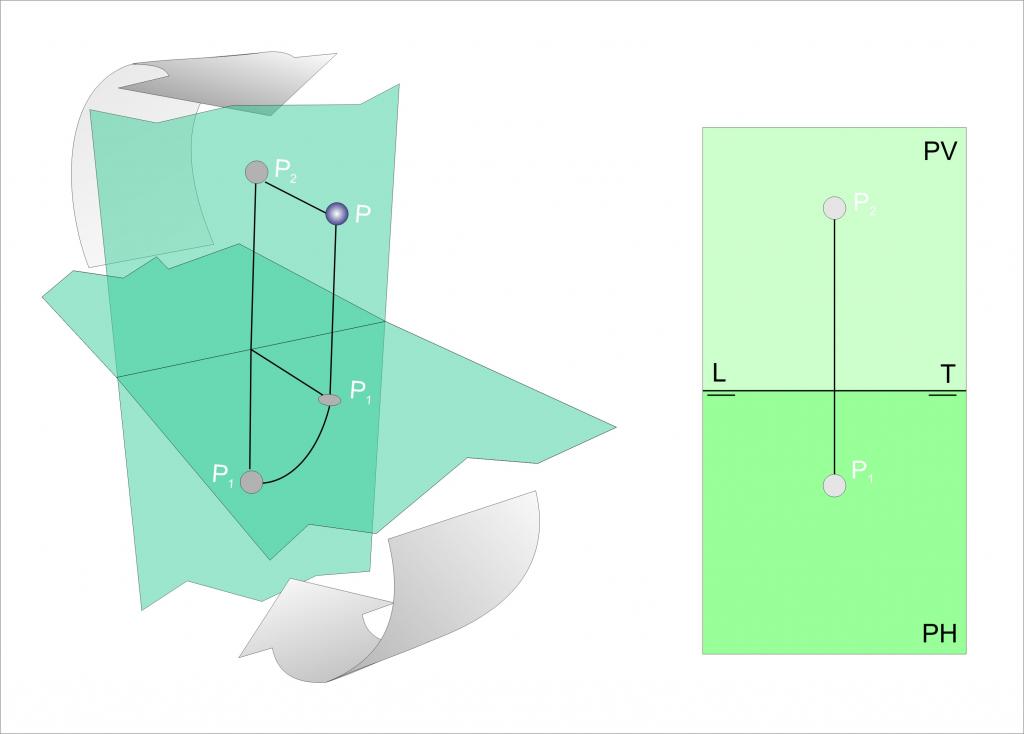
Сега разгледайте каква е проекцията на точка, дадена в пространството на определена равнина. Лесно е да се предположи, че тази проекция е и точка, която заедно с оригиналната образува вектор перпендикулярно на равнината.
Да предположим, че проекцията в равнината на координатите на точката М има следното:
M 1 (x 1 ; y 1 ; z 1 )
Самата равнина се описва чрез уравнението:
A * x + B * y + C * z + D = 0
Въз основа на тези данни, можем да направим уравнението на права линия, пресичаща равнината под прав ъгъл и преминавайки през М и М 1 :
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (A; B; C)
Тук променливите с нулеви индекси са координатите на точката М. Възможно е да се изчисли позицията в равнината на точката M 1 при предположението, че нейните координати трябва да удовлетворяват и двете писмени уравнения. Ако тези уравнения не са достатъчни за решаване на проблема, тогава може да се използва условието за паралелизъм MM 1 ¯ и вектора на посоката за дадена равнина.
Очевидно е, че проекцията на точка, принадлежаща на равнина, съвпада със себе си, а съответното разстояние е нула.
Задача с точка и равнина
Нека дадена точка M (1; -1; 3) и равнината, която е описана със следното общо уравнение:
-x + 3 * y -2 * z + 4 = 0
Необходимо е да се изчислят координатите на проекцията в равнината на точката и да се изчисли разстоянието между тези геометрични обекти.
Първо, ние конструираме уравнението на линия, минаваща през М и перпендикулярна на посочената равнина. Тя изглежда така:
(x; y; z) = (1; -1; 3) + α * (- 1; 3; -2)
Означаваме точката, в която тази права линия пресича равнината, M1. Равенства за равнина и права линия трябва да бъдат изпълнени, ако заместим M 1 координатите в тях. Като пишем изрично формулата на права линия, получаваме следните четири уравнения:
-x 1 + 3 * y 1 -2 * z 1 + 4 = 0;
х 1 = 1 - а;
у 1 = -1 + 3 * а;
z 1 = 3 - 2 * a
От последното равенство получаваме параметъра α, след което го заместваме в предпоследния и втория израз, получаваме:
a = (3-z1) / 2;
у 1 = -1 + 3 * (3-z 1 ) / 2 = -3 / 2 * z 1 + 3.5;
x 1 = 1 - (3-z 1 ) / 2 = 1/2 * z 1 - 1/2
Изразът за у 1 и х 1 се заменя в уравнението за равнината, имаме:
-1 * (1/2 * z 1 - 1/2) + 3 * (- 3/2 * z 1 + 3.5) -2 * z 1 + 4 = 0
Къде получаваме:
z 1 = 15/7
След това:
у 1 = -3 / 2 * 15/7 + 3.5 = 2/7;
x 1 = 1/2 * 15/7 - 1/2 = 4/7
Установихме, че проекцията на точката М върху дадена равнина съответства на координатите (4/7; 2/7; 15/7).
Сега изчислете разстоянието | MM 1 ¯ |. Координатите на съответния вектор са:
ММ 1 ¯ (-3/7; 9/7; -6/7)
Необходимото разстояние е:
d = | MM 1 ¯ | = /126 / 7 ≈ 1.6
Три точки на проекция
По време на производството на чертежи често е необходимо да се получат издатини на секции върху взаимно перпендикулярни три равнини. Следователно е полезно да се помисли какви ще бъдат проекциите на определена точка M с координати (x 0 ; y 0 ; z 0 ) върху три координатни равнини.

Не е трудно да се покаже, че xy равнината е описана с уравнението z = 0, xz равнината съответства на израза y = 0, а оставащата yz равнина е означена с равенството x = 0. Лесно е да се предположи, че проекциите на точка на 3 равнини ще бъдат равни:
за х = 0: (0; y 0 ; z 0 );
за у = 0: (х 0 ; 0; z 0 );
за z = 0: (x 0 ; y 0 ; 0)
Къде е важно да се знаят проекциите на точката и разстоянието до равнините?
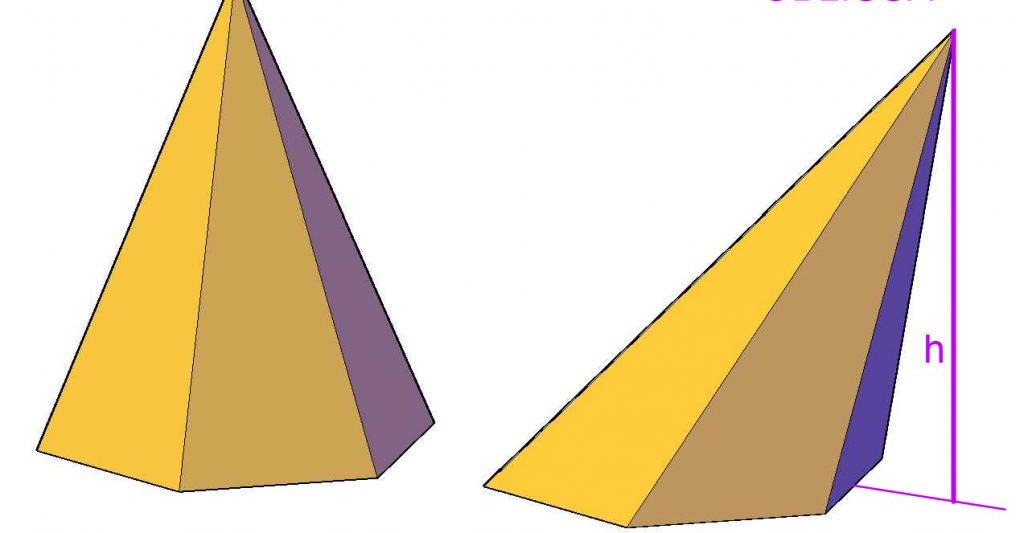
Определянето на положението на проекцията на точки върху дадена равнина е важно при намирането на такива величини като площ и обем за наклонени призми и пирамиди. Например, разстоянието от върха на пирамидата до равнината на основата е височината. Последното е включено във формулата за обема на тази цифра.
Разглежданите формули и методи за определяне на проекциите и разстоянията от една точка до права и равнината са доста прости. Важно е само да се запомнят съответните форми на равнинните и директните уравнения, както и да се получи добро пространствено въображение, за да могат да се прилагат успешно.