Законът на еквивалентите: формула и формулировка. Закон за химичните еквиваленти

В края на XVIII век много от законите на химията са получени емпирично. Те могат да бъдат използвани и приложени на практика, но точни доказателства са получени едва много десетилетия по-късно. Един от тези стълбове на съвременната химия е законът на еквивалентите, който е пряко свързан с други основни закони - законът за запазване на масата и правилото на множествените отношения.

праистория

Основата на новата позиция вече е била известна в края на XVIII век, законът за постоянния състав, наричан по-късно закон за опазване на масата. Благодарение на него беше установено, че различни химикали могат да взаимодействат не произволно, а в строго определени пропорции. Следователно думата "еквивалентност" се появява в химическия речник. Новата концепция в превод на руски означава "еквивалентност". Това беше първата стъпка към създаването на правило, което по-късно стана известно като закон на еквивалентите. Многобройни експерименти по-късно многократно потвърждаваха теоретичните предположения.

Ново правило

Законът за еквивалентите в химията променя формулата му няколко пъти. В съвременните учебници тя е написана както следва:

• "Еквивалентът на всеки елемент се счита за такова количество, което може да се свърже с един мол водород."

Такава формулировка на закона на еквивалентите е универсална и се използва в училищната химия и в сериозни научни експерименти. Например, за известно съединение, НС1, еквивалентът на хлор съответства на една молитва, а на съединения с H2S, Н20, еквиваленти за сяра и кислород ще бъдат равни на ½ мола и т.н. В съединенията от вида Hn X, където Н е водород, X е друг химичен елемент, п е количеството водород в молекулата, еквивалентът на елемент X винаги ще бъде равен на 1 / n mol. Този закон на еквивалентите в химията се простира до прости вещества, в които водородът взаимодейства с един елемент, и до съединения, в които водородът е в съседство с много други атоми.

Еквивалентна маса

Сключването на новия закон е нова концепция за масата. Новият термин стана много удобен за измерване на промяната на веществото в реакциите. Еквивалентната маса се нарича маса 1 еквивалент. Така законът на еквивалентите предсказва масата на друг елемент дори без лабораторни изследвания. В дадения пример на съединение на солна киселина еквивалентната хлорна маса е 34.45 g / mol. В съединението Н20, еквивалентната маса на кислорода ще бъде 16: 2 = 8 g / mol, и така нататък.

Как може да се изчисли това

Еквивалентната маса може да бъде изчислена чрез анализиране на получените съединения. Не е необходимо да се комбинира с тестваното вещество с водород, за да се изчисли еквивалентната маса. Законът на еквивалентите потвърждава, че е достатъчно да се знае съставът на съединението на даден елемент и еквивалентната маса на друг елемент, с който е свързана нашата неизвестна проба. Пример за намиране на еквивалента е следната задача:

Съединение 3 g натрий с излишък от хлор образува 7.62 g натриев хлорид (натриев хлорид). Открийте еквивалентната маса на натрия, ако e _Cl = 35.45 g / mol.

От условието на проблема следва, че в продукта на реакцията, трапезната сол, 3 g натрий представлява 7.62 - 3 = 4.62 g хлор. Оттук и заключението:

E _Na = 3 х 35.45: 4,62 = 23 g / mol.

Моларна маса натрий се определя лесно от периодичната таблица. Тя е равна на 23 g / mol. От това следва, че еквивалентната маса на натрия е равна на една молитва.

Трудни елементи

Живата и неодушевена природа, която ни заобикаля, се състои от много различни вещества и повечето от тях са сложни. Следователно, еквивалентите често се определят по различен начин, в зависимост от състава, от който съседно вещество са получени. Но във всички проучени случаи различните еквиваленти се третираха като малки цели числа. Например, достатъчно е да се приемат такива известни съединения като оксид и серен диоксид. Еквивалентните маси на този елемент, изчислени по горния метод, дават стойности от 16 g / mol и 32 g / mol. Но съотношението на тези стойности се свежда до проста форма от 1: 2.

Това правило е извлечено емпирично от известния английски химик, лекар и натуралист. От Джон Далтън Самоукият учител, който създава странни експерименти, първоначално ужасяваше слугите и караше съседите да се смеят. Въпреки това той поставяше простите си експерименти и потвърждаваше много научни предположения. Законът за множествените взаимоотношения първо е бил формулиран от него.

Законът на еквивалентите се прилага за сложни съединения, в които взаимодействат няколко елемента. Понятието за еквивалент на един от елементите в комплексната комбинация престава да бъде недвусмислено. За такива съединения формулировката на закона за еквиваленти звучи малко по-различно: "Като еквивалент на комплексно вещество се използва такова количество, което ще участва в химична реакция без остатък с един еквивалент на елемент или комплексно съединение, или с един еквивалент водород."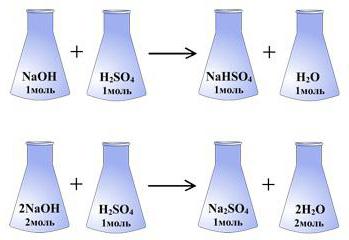

Това правило се използва навсякъде. Ако премахнете тромавите дефиниции, той може да се сведе до следната позиция: "Различните вещества могат да реагират само в количества, които са пропорционални на техните еквиваленти."

решения

При проучването и подготовката на решенията всички горепосочени закони са напълно приложими. Тук ролята на еквивалента се играе от новата единица, която се нарича г / еквивалент. Това е името на количеството вещество, от което една частица (атом или йон) е химически еквивалентна на атом или водороден йон. Така законът на еквивалентите за решения звучи подобно на класическата дефиниция.

Общ закон за еквиваленти

Формулата за еквиваленти на различни съединения като цяло е, както следва:

• E = моларна маса / (брой атоми на елемента × валентност).

Както може да се види, еквивалентността е пряко зависима от моларната маса на веществото и от неговата валентност. Ако химикът има информация за еквивалентите на неизвестни елементи, той може да определи способността си да влиза в химични реакции. При известно количество грамове / еквиваленти от дадено вещество, учен може незабавно да направи заключение за концентрацията и свойствата на дадено решение.

стехиометрия

Количественият състав на веществата и техните съотношения в съединенията е посветен на отделен раздел на химията, наречен стехиометрия. Задачите на този раздел на теоретичната химия са да се изчислят количествените съотношения в съединенията. За прости вещества това е доста просто, а за сложни вещества, протеини или вируси стехиометричните изчисления стават много трудна задача.