Историята на Питагоровата теорема. Доказателство на теоремата

Тези, които се интересуват от историята на Питагоровата теорема, която се изучава в учебната програма, също ще бъдат любопитни за факта, че през 1940 г. ще бъде публикувана книга с триста и седемдесет доказателства за тази привидно проста теорема. Но тя заинтригувала умовете на много математици и философи от различни епохи. В Книгата на рекордите на Гинес тя е фиксирана като теорема с максималния брой доказателства.

Историята на Питагоровата теорема

Свързан с името на Питагор, теоремата е известна много преди раждането на великия философ. Така, в Египет, по време на изграждането на структурите, съотношението на правоъгълен триъгълник преди пет хиляди години беше взето под внимание. Вавилонските текстове се отнасят до същата пропорция. правоъгълен триъгълник 1200 години преди раждането на Питагор.

Възниква въпросът защо тогава историята казва - появата на Питагоровата теорема принадлежи на него? Отговорът може да бъде само един - той доказа съотношението в триъгълника. Той правеше това, което преди векове онези, които просто използваха съотношението на аспектите и хипотенузата, установени емпирично не го направиха.

От живота на Питагор

Голямо бъдеще учен, математик, Философът е роден на остров Самос през 570 г. пр. Хр. Исторически документи съхраняват информация за бащата на Питагор, който е бил резбар от скъпоценни камъни, но няма информация за майката. Беше казано за роденото момче, че е извънредно дете, което от детството си проявява страст към музиката и поезията. Историците приписват учителите на младия Питагор на Хердомадант и Ферекид от Сирос. Първият представи момчето в света на музите, а вторият - като философ и основател на италианската философска школа - насочи погледа на младежа към лога.

На 22-годишна възраст (548 г. пр. Хр.) Питагор отишъл в Ноукратис да изучава езика и религията на египтяните. По-нататък пътят му лежеше в Мемфис, където благодарение на свещениците, след като преминаваше през гениалните си изпитания, той разбира египетската геометрия, която вероятно подтикна любознателния младеж да докаже теоремата на Питагорей. Историята ще припише тази теорема на теоремата в бъдеще.

Заловен от царя Вавилон

По пътя за Елада Питагор е заловен от царя Вавилон. Но да бъдеш в плен ползваше любопитния ум на начинаещ математик, той имаше какво да научи. Всъщност в тези години математиката във Вавилон е по-развита, отколкото в Египет. Той прекара дванадесет години в изучаването на математика, геометрия и магия. И, вероятно, именно Вавилонската геометрия беше включена в доказателството на съотношението на триъгълника и историята на откриването на теоремата. Питагор имаше достатъчно знания и време за това. Но това се случи във Вавилон, няма документално потвърждение или опровержение.

През 530 г. пр. Хр Питагор бяга от плен в родината си, където живее в двора на тиранин Поликрат в статут на полу-плоча. Такъв живот не отговаря на Питагор и той се оттегля в пещерите на Самос, а след това отива в южната част на Италия, където по това време се намира гръцката колония Кротон.

Тайният монашески ред

На базата на тази колония Питагор организира таен монашески орден, който е едновременно религиозен съюз и научно общество. Това общество има своя собствена харта, която се отнася до спазването на определен начин на живот.

Питагор твърди, че за да разбере Бог, човек трябва да научи такива науки като алгебра и геометрия, да познава астрономията и да разбира музиката. Изследователската работа е сведена до познаването на мистичната страна на числата и философията. Трябва да се отбележи, че принципите, проповядвани от Питагор по това време, имат смисъл в имитация дори и сега.

Много от откритията, направени от учениците на Питагор, са му приписани. Въпреки това, ако говорим накратко, историята на създаването на Питагоровата теорема от древните историци и биографи на времето, се свързва директно с името на този философ, мислител и математик.

Учения на Питагор

Може би мисълта за връзката на теоремата с името на Питагор накара историците да кажат великия грък, че всички явления на нашия живот са кодирани в известния триъгълник с краката и хипотенузата. И този триъгълник е "ключът" за решаването на всички възникващи проблеми. Великият философ казва, че трябва да се види един триъгълник, тогава можем да предположим, че проблемът е решен с две трети.

Питагор говори за учението си само устно на учениците си, без да прави бележки, да го пази в тайна. За съжаление учението на най-великия философ не е оцеляло и до днес. Нещо от него е изтекло, но не може да се каже колко е вярно и колко е невярно в това, което е станало известно. Дори и с историята на Питагоровата теорема, не всичко е безспорно. Историците на математиката се съмняват в авторството на Питагор, според тях теоремата е била използвана много векове преди нейното раждане.

Питагорова теорема

Може да изглежда странно, но няма исторически доказателства за теоремата от самия Питагор - не в архивите, нито в други източници. В модерната версия се счита, че той принадлежи на никой друг, освен на самия Евклид.

Има доказателства за един от най-великите историци на математиката, Мориц Кантор, който е открил на папируса, съхраняван в Берлинския музей, записан от египтяните около 2300 г. пр. Хр. д. равенство, което гласи: 3² + 4² = 5².

Накратко от историята на Питагоровата теорема

Формулирането на теоремата от евклидовите "Принципи" в превода звучи същото като в съвременната интерпретация. Няма ново четене в него: квадратът на противоположната страна на десния ъгъл е равен на сумата от квадратите на страните, съседни на десния ъгъл. Фактът, че древните цивилизации на Индия и Китай са използвали теоремата, са потвърдени от трактата Джоу би суан джин. Той съдържа информация за египетския триъгълник, който описва съотношението на страниците като 3: 4: 5.

Не по-малко интересна е и друга китайска математическа книга, Chu-Pei, в която се споменава и питагорейският триъгълник с обяснение и рисунки, които съвпадат с рисунките на индуската геометрия на Bashara. За самия триъгълник в книгата е написано, че ако десният ъгъл може да бъде разложен на съставните му части, то линията, която свързва краищата на страните, ще бъде равна на пет, ако основата е три, а височината е четири.

Индийският трактат "Сулва сутра", датиращ от VII-V в. Пр. Хр. говори за изграждане на прав ъгъл, използвайки египетския триъгълник.

Доказателство на теоремата

През средните векове студентите считат, че доказателството на теоремата е твърде трудно. Слабите ученици запомняха теореми наизуст, без да разбират смисъла на доказателството. В това отношение те получиха прякора "магарета", защото Питагоровата теорема беше непреодолимо препятствие за тях, като мост за задник. През Средновековието учениците измислиха шеговито стихове по темата на тази теорема.

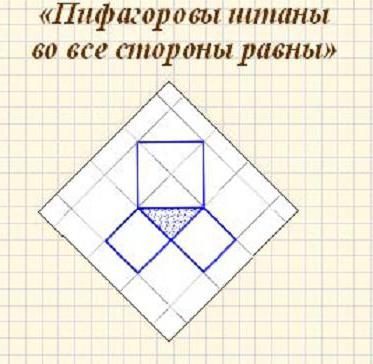
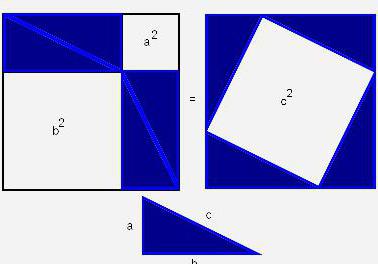
За да се докаже Питагоровата теорема по най-лесния начин, човек просто трябва да измери неговите страни, без да използва концепцията за квадратите в доказателството. Дължината на страната, която е противоположна на десния ъгъл, е c, а съседните a и b в резултат получават уравнението: a ² + b ² = c ² . Това твърдение, както бе споменато по-горе, се проверява чрез измерване на дължините на страните на правилния триъгълник.

Ако започнем да докажем теоремата, като разгледаме площта на правоъгълниците, построени по страните на триъгълника, можем да определим площта на цялата фигура. Тя ще бъде равна на площта на квадрата със страната (a + b), а от друга страна, сумата от площите на четирите триъгълника и вътрешния квадрат.

(a + b) ² = 4 x ab / 2 + c ² ;

a ² + 2ab + b2;

c ² = a ² + b ² , както се изисква.

Практическото значение на Питагоровата теорема е, че тя може да се използва за намиране на дължините на сегментите, без да ги измерва. При изграждането на сградите се изчисляват разстоянията, разположението на опорите и гредите, определят се центровете на тежестта. Питагоровата теорема се използва във всички съвременни технологии. Ние не забравихме теоремата при създаването на филми в 3D-6D-измерения, където в допълнение към трите обичайни стойности: височина, дължина, ширина - време, миризма и вкус се вземат предвид. Как вкусовете и миризмите са свързани с теоремата - питаш? Много е просто - когато покажете филм, трябва да изчислите къде и какво мирише и вкус да изпратите в залата.

Дали все още ще бъде. Неограничено пространство за откриване и създаване на нови технологии очаква очакване на умове.