Концепцията за ъгловия импулс, неговият закон за запазване и пример за решаване на проблема
Ротационното движение е не по-малко разпространено в природата от линейното движение на обектите. За да се провери това, достатъчно е да си припомним въртенето на колелата на коли и велосипеди, остриетата на хеликоптерите и феновете, планетите около неговата ос и около неговите звезди. Да се опише процесът на кръговото движение на обекти, използвайки физическа величина, която се нарича "ъглово движение". Помислете в статията какво е то.
Импулсен момент на частицата и оста на въртене
По-долу е показан чертеж, който схематично показва, че частица или материална точка на маса m се движи по кръгова траектория с радиус ¯ с скорост ν, насочена тангенциално. Оста на въртене е перпендикулярна на равнината на фигурата в точка О.
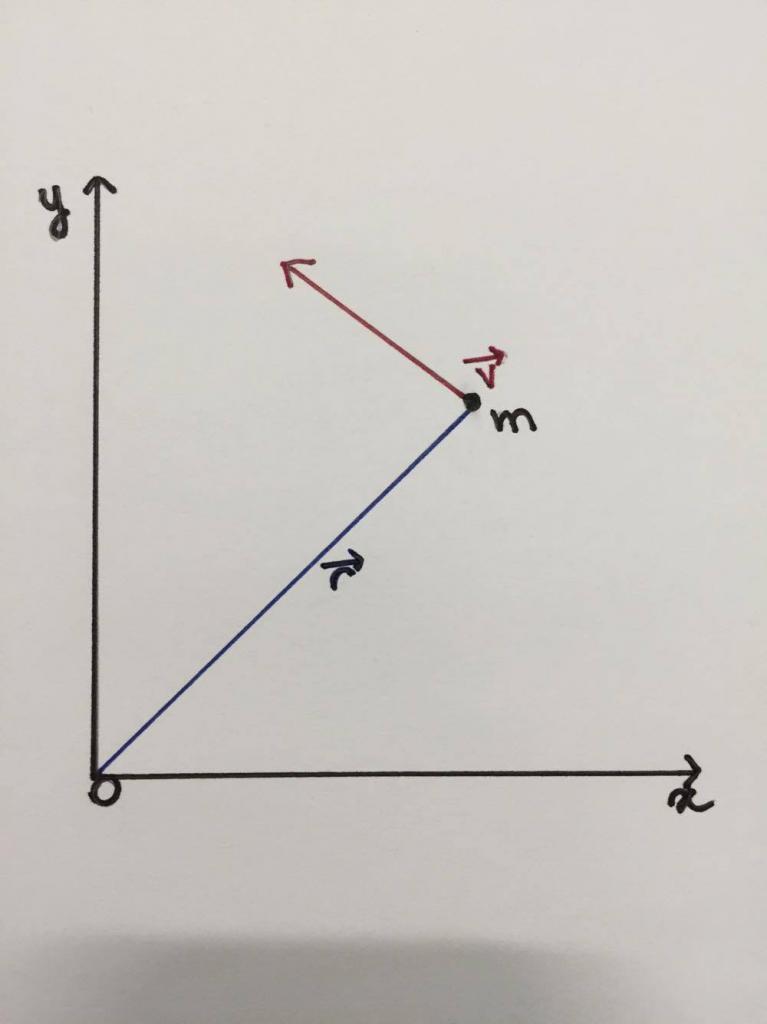
Въвеждаме следната физическа величина:
L¯ = r¯ * m * v¯ = r¯ * p¯.
Нарича се ъгловият импулс или ъгловия импулс. Както виждате, това е векторно количество. Нейната посока може да бъде определена от правилото на дясната ръка: трябва да насочите 4 пръста така, че те, движейки се по вектор r¯, да стигнат до края на вектора p¯ (или v¯), след това палецът ще покаже посоката L¯. В този случай, L¯ е насочен към четеца перпендикулярно на равнината на чертежа.
Тъй като скоростта на частиците (инерция) във фигурата е насочена под прав ъгъл спрямо вектора ¯, намаленото уравнение може да бъде пренаписано в скаларна форма:
L = r * m * v = r * p.
Ъгловата скорост и инерционният момент
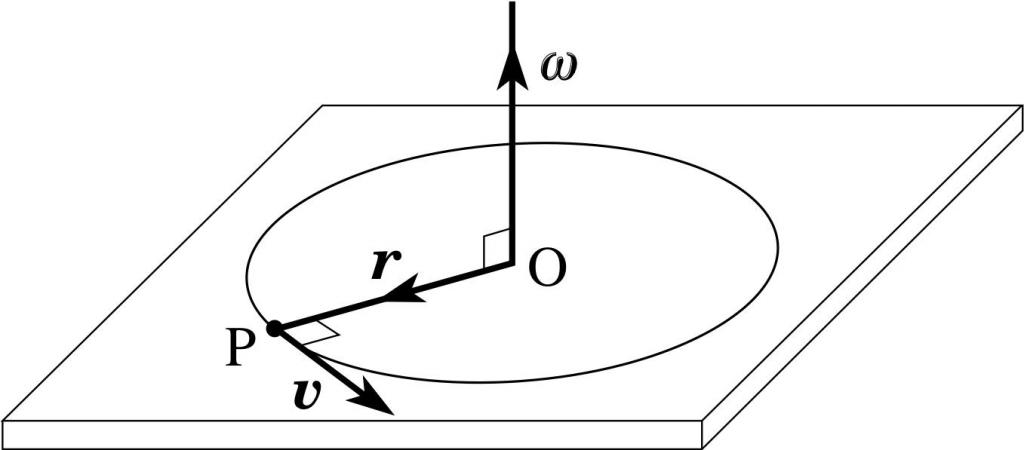
Инерцията на частица от предишния пример може да бъде записана през ъгловата скорост ω. За да направим това, използваме връзката й с линейната скорост:
ω = v / r => v = ω * r.
Подставяйки последното уравнение в скаларно уравнение за L, получаваме:
L = r 2 * m * ω = I * ω, където I = r 2 * m.
Тук I е моментът на инерцията на частицата. Полученият израз често се използва за решаване на практически проблеми, единият от които ще бъде разгледан по-долу.
Законът за запазване на въртеливото движение

Движението в кръг, както и линейното движение на обекти в пространството, се характеризират с закони за опазване. Един от тях е запазването на ъгловия импулс. Получаваме този закон.
Уравнението на разглеждания тип движение има следната форма:
dL / dt = M.
Където dL / dt характеризира промяната на ъгловия момент на тялото с течение на времето, когато тя е повлияна от определен момент М, създадена от външни (а не вътрешни) сили. Ако този момент на сила е нула, то лявата страна на израза изчезва, което означава L = const. За този случай можем да напишем следното равенство:
L = const = I 1 * ω 1 = I 2 * ω 2 .
Какво означава този запис? Той казва, че ако някое тяло се върти със скорост ω 1 и имаше момент на инерция I 1 , то поради някои вътрешни (не външни) сили моментът на инерцията се промени и стана равен на I 2 , тогава новата скорост на въртене ω 2 ще бъде пропорционална свързани с тази промяна.
Записаното отношение се нарича законът за запазване на ъгловия момент на точка (тяло) по аналогия със съответния закон за линейни величини (запазване на инерцията), тъй като моментът на инерцията I играе ролята на маса, а ъгловата стойност ω играе ролята на маса.
Използвайки закона L = const
Отношението, разглеждано в предишния параграф, може да се види в действие, когато се изпълняват скейтъри или балерини. Извършвайки сложна акробатика, те завъртат телата си, разпръскват ръцете и краката си и след това притискат крайниците си към тялото. Последното действие води до намаляване на стойността на I и съответно до увеличаване на скоростта на въртене, което създава доста ефектен ефект.

Друг пример за използването на неизменяемостта на ъгловия момент на системата е осъществяването на въртенето на изкуствен спътник в космическото пространство. За да направите това, изпълнете специален маховик, прикрепен към него. Тъй като общото ъглово движение не трябва да се променя поради действието на вътрешните сили, самият сателит започва да се върти в обратна посока. Веднага щом се обърне към желания ъгъл около своята ос, маховикът се спира с помощта на електрически двигател, а тялото на спътника също спира своето въртене.
Изчислете момента на инерцията
Тъй като стойността на I присъства в закона за запазване на кръговото движение, трябва да кажем няколко думи за него. Той характеризира инерцията на системата, т.е. колко "трудна" или "лесна" е тя да я освободи. Например, маховикът на автомобила има голяма маса и относително голям радиус, така че инерционният му момент е значителен. Напротив, колелото на велосипеда е изработено от алуминиева светлина, така че за него аз ще бъда сравнително малък.
За да изчислите тази физическа характеристика, използвайте формулата:
I = ( m (r 2 * dm).
Откъдето се вижда, че моментът на инерцията е характеристика на системата, в която влиза тялото на революцията, а не самото тяло. Това я отличава от линейната инерция, която зависи единствено от свойствата на тялото (неговата маса).
Задача с въртящ се прът
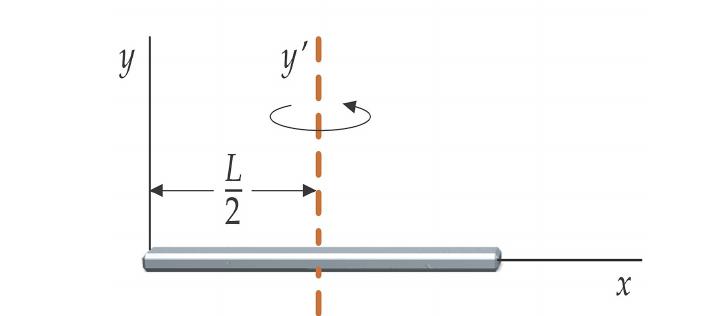
Ще решим един интересен проблем: има твърд прът, който се върти около оста, разположен в края му. Ако тази ос е плавно изместена към центъра на масата на пръта, как ще се промени нейната скорост на въртене?
Това е класическа задача за прилагане на закона за запазване на ъгловия импулс. Трудността се състои в изчисляване на промяната в момента на инерцията. За да направите това, можете да използвате горната формула с интеграл, но ще бъде по-лесно да погледнете необходимите стойности на I в референтната литература.
В началото оста на въртене преминаваше през края на пръта. За тази система моментът на инерция е равен на:
I 1 = m * L 2/3, където L е дължината на пръта, m е неговата маса.
Когато оста се измести към центъра на масата на обекта, моментът му на инерция се промени, станал равен на:
I2 = m * L 2/12.
Приложете закона за запазване за L, получаваме:
m * L 2/3 * ω 1 = m * L 2/12 * ω 2 => ω 2 / ω 1 = m * L 2/3 / (m * L 2/12) = 4.
Получихме отговор на проблема: пръчката ще се върти 4 пъти по-бързо, отколкото в началото.