Тялото беше хвърлено под ъгъл към хоризонта: скорост, обхват и височина

В тази статия ще анализираме ситуацията, когато тялото е хвърлено под ъгъл към хоризонта. Това може да е хвърляне с ръка, изстрел от оръдие, изстрелване на стрела от лък и т.н. Всички споменати ситуации са описани еднакво от математическа гледна точка.

Характеристика на движение под ъгъл спрямо хоризонта

Какви са приликите на горните примери от гледна точка на физиката? Тя се крие в характера на силите, действащи върху тялото. По време на свободния полет на дадено тяло върху него действат само две сили:

• Gravity.
• Въздушно съпротивление

Ако телесното тегло е достатъчно голямо и формата му е заострена (снаряд, стрелка), тогава въздушното съпротивление може да бъде пренебрегнато.

Така движението на обект, хвърлен под ъгъл към хоризонта на тялото, е задача, в която се появява само силата на гравитацията. Това определя формата на траекторията, която се описва с добра точност чрез параболична функция.

Уравнения за движение по параболична траектория. Скорост

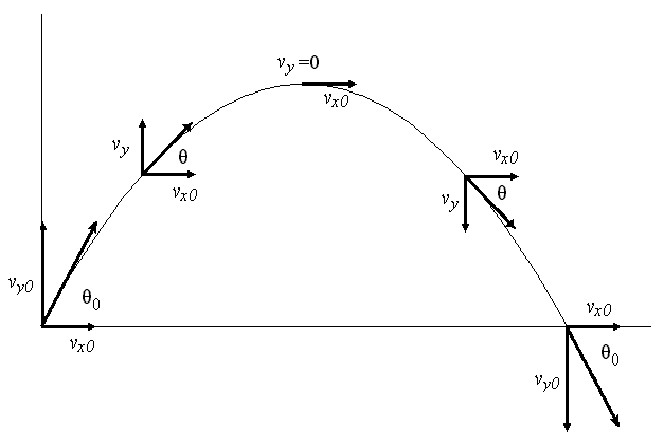
Тялото е хвърлено под ъгъл към хоризонта. Как можете да опишете неговото движение? Тъй като единствената сила, действаща по време на полета на тялото, е насочена надолу, нейната хоризонтална компонента е нула. Това означава, че хоризонталното движение на даден обект се определя еднозначно от началните условия (ъгъл на хвърляне или изстрел θ и скорост v). Вертикалното движение на тялото е ярък пример за равномерно ускорено движение, при което константата g играе роля в ускорението (9,81 m / s ² ).

Като се има предвид горното, можем да напишем два компонента за скоростта на летящото тяло във време t:

v _x = v * cos (θ);

v _y = v * sin (θ) - g * t

Както може да се види, компонентът v _x не зависи от времето и остава постоянен през цялата траектория на полета (поради липсата на външни сили в посоката на оста x). Компонент v _y има максимум в началния момент от времето. И тогава започва да намалява до точката, че изчезва при максималната точка на излитане на тялото. След това той променя знака си и по време на падането се оказва равен на модула на началния компонент v _y , т.е. v * sin (θ).

Писмените уравнения ни позволяват да определим скоростта на тялото, хвърлено под ъгъл към хоризонта във всеки момент t. Модулът му ще бъде равен на:

v = √ (v _x ² + v _y ² ) = √ (v ² * cos ² (θ) + v ² * sin ² (θ) - 2 * v * sin (θ) * g * t + g ² * t ² ) =

= √ (v ² - 2 * v * sin (θ) * g * t + g ² * t ² )

Уравнения за движение по параболична траектория. Обхват на полета

Тялото е хвърлено под ъгъл към хоризонта. Какво разстояние ще лети? Въпросът за обхвата на полета се отнася до промяната на x координатите. Възможно е да се намери тази стойност, ако интегрираме двата компонента на скоростта във времето. В резултат на интеграцията получаваме формулите:

x = v * cos (θ) * t + x ₀ ;

y = v * sin (θ) * t - g * t 2/2 + y ₀

Разликата в координатите x и x ₀ е диапазонът. Ако приемем, че х ₀ = 0, тогава диапазонът ще бъде равен на х, за да се намери кой трябва да знаете колко дълго тялото ще бъде във въздуха.

Второто уравнение позволява да се изчисли това време, при условие че стойността на y _{0 е} известна (височина h, от която тялото е хвърлено). Когато обектът завърши движението си (пада на земята), неговата y координата ще се превърне в нула. Изчислете времето, когато това се случи. Имаме:

v * sin (θ) * t - g * t 2/2 + h = 0

Пред нас е пълно квадратно равенство. Решаваме го чрез дискриминант:

D = v ² * sin ² (θ) - 4 * (-g / 2) * h = v ² * sin ² (θ) + 2 * g * h;

t = (-v * sin (θ) ± √D) / (2 * (-g / 2))

Отхвърляме отрицателния корен. Получаваме следното време за полета:

t = (v * sin (θ) + √ (v ² * sin ² (θ) + 2 * g * h)) / g

Сега ще заместим тази стойност с равенство за полетния диапазон. Получаваме:

x = v * cos (θ) * (v * sin (θ) + √ (v ² * sin ² (θ) + 2 * g * h)) / g

Ако тялото е изхвърлено от земята, т.е. h = 0, тогава тази формула ще бъде много по-проста. И вземете формата:

x = 2 * v ² * cos (θ) * sin (θ) / g = v ² * sin (2 * θ) / g

Последната експресия се получава, като се използва връзката между тригонометричните функции на синуса и косинуса (формула за редукция).

Тъй като синусът има максимална стойност за прав ъгъл, тогава максималният обхват се достига, когато тялото е хвърлено (изстрел) от земята под ъгъл от 45 °, и този диапазон е равен на:

х = v2 / g

Височината на тялото, хвърлена под ъгъл към хоризонта

Сега ние дефинираме друг важен параметър - височината, до която може да се изкачи изоставен обект. Очевидно е, че за да се направи това, достатъчно е да се разгледа само една промяна в координатата y.

И така, тялото беше хвърлено под ъгъл към хоризонта, до каква височина щеше да излезе? Тази височина ще съответства на равенството на нула на компонентата на скоростта v _y . Имаме уравнението:

v _y = v * sin (θ) - g * t = 0

Решете уравнението. Получаваме:

t = v * sin (θ) / g

Сега трябва да замените това време в израза за y координатата. Получаваме:

y = v * sin (θ) * t - g * t 2/2 + h = v ² * sin ² (θ) / g - g / 2 * v ² * sin ² (θ) / g ² + h =

= v ² * sin ² (θ) / (2 * g) + h

Тази формула предполага, че максималната височина, за разлика от обхвата на полета, се получава чрез изхвърляне на тялото вертикално (θ = 90). В този случай стигаме до формулата:

у = v ² / (2 * g) + h

Любопитно е да се отбележи, че във всички формули, дадени в тази статия, телесната маса не се появява. Характеристиките на параболичната траектория са независими от нея, но само при липса на съпротивление на въздуха.